22.5 综合与实践 测量与误差同步作业
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.5 综合与实践 测量与误差同步作业
姓名:__________班级:__________考号:__________
一 、选择题
如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)
A、4 B、5 C、6 D、8
数学兴趣小组的小明想测量教学楼前的一棵树的高度.下午课外活动时他测得一根长为1m的竹竿的影长是0.8m.但当他马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图).他先测得留在墙壁上的树影高为1.2m,又测得地面的影长为2.6m,请你帮他算一下,下列哪个数字最接近树高( )m.
A、3.04 B、4.45 C、4.75 D、3.8
如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
A、3倍 B、不知AB的长度,无法计算 C、 D、
小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O, 准星A, 目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到 ,若OA=0.2米,OB=40米, =0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为( )
A、3米 B、0.3米 C、0.03米 D、0.2米
一个油桶高0.8m , 桶内有油,一根长lm的木棒从桶盖小口插入桶内,一端到达桶底,另一端恰好在小口处,抽出木棒量得浸油部分长0.8m,则油桶内的油的高度是( )
A、0.8m B、0.64m C、1m D、0.7m
为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A.10m B.12m C.12.4m D.12.32m
如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC, 则梯子的长为( )
A、3.5m B、3.85m C、4m D、4.2m
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A. B. C. D.6
二、填空题
如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE , 已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=________m.
为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 米.
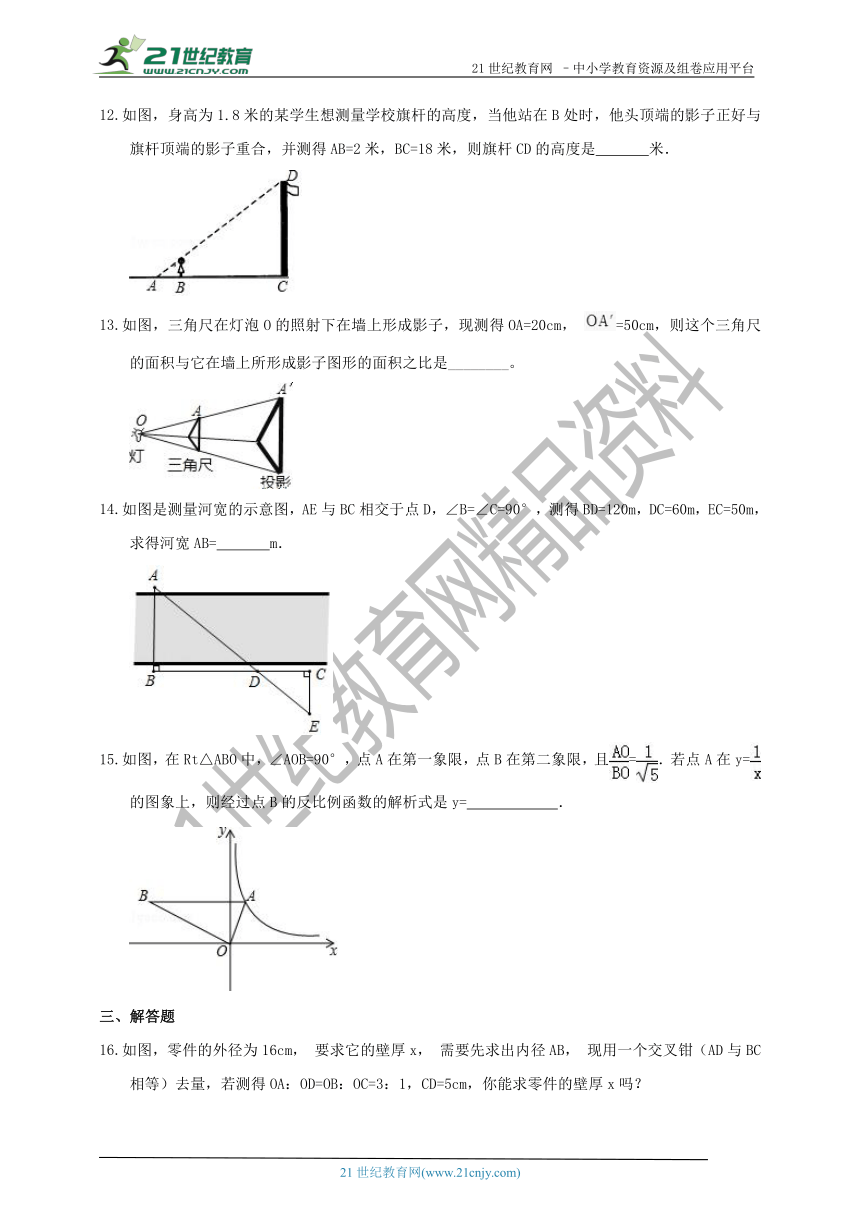
如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是 米.
如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm, =50cm,则这个三角尺的面积与它在墙上所形成影子图形的面积之比是________。
如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= m.
如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且=.若点A在y=的图象上,则经过点B的反比例函数的解析式是y= .
三、解答题
如图,零件的外径为16cm, 要求它的壁厚x, 需要先求出内径AB, 现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,CD=5cm,你能求零件的壁厚x吗?
某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=10m,塔影长DE=20m,小惠和小岚的身高都是1.60m,同一时刻,小惠站在点E处,影子在坡面上,小岚站在平地上,影子也在平地上,两人的影长分别是2m和1m,试求塔高AB.
如图所示,竖杆AC、BD的长度分别为200cm、300cm,CD=300cm.现有一男生站在斜杆AB下方的点E处,设CE=x(cm),从E处跳起的摸高EF=y(cm).
(1)求y与x之间的函数关系式;
(2)若245(cm)≤y<255(cm)时,求该男生跳起时站的位置x(cm)的范围.
小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
如图,△ABC是一锐角三角形余料,边BC=16cm,高AD=24cm,要加工成矩形零件,使矩形的一边在BC上,其余两个顶点E、F分别在AB、AC上.
求:(1)AK为何值时,矩形EFGH是正方形?
(2)若设AK=x,SEFGH=y,试写出y与x的函数解析式.
(3)x为何值时,SEFGH达到最大值.
答案解析
一 、选择题
【考点】相似三角形的应用
【分析】由题意得出,△ABC∽△ADE , 利用对应边成比例列方程代入相应数数据求解.
解:如图,由图可知,
∵BC∥ED ,
∴△ABC∽△ADE ,
∴ ,
又DE=10米,AF=3,FG=2米,
∴AG=AF+FG=5米
即 ,
解得BC=6米
故选:C.
【考点】相似三角形的应用
【分析】此题先求出这棵树全落在地面上时的影子的长,再根据在同一时刻物高与影长对应成比例列出方程,解方程求出这棵树的高度.
解:∵留在墙壁上的树影高为1.2m,∴这段影子在地面上的长为:1.2×0.8=0.96(m),
∴这棵树全落在地面上时的影子的长为:2.6+0.96=3.56(m),
∴设这棵树的高度为xm,则 ,解得x=3.56÷0.8=4.45,
∴设这棵树的高度为4.45m.
故选:B.
【考点】相似三角形的应用
【分析】由AB∥A′B′可知,△OAB∽△OA′B′,根据相似三角形的相似比等于对应边上高的比,列方程求解.
解:如图,作OM⊥AB , ON⊥ , ∵AB∥ ,
∴△OAB∽△ ,
∴ ,
即 ,
∴ = AB .
故选:C.
【考点】相似三角形的应用
【分析】由题意可知,准星和靶是平行的,把实际问题抽象到相似三角形中,根据两三角形相似的对应边成比例列出方程,通过解方程可求出偏离的距离.
解:∵ ∥ ∴OA:OB= :
∴
解得: =0.3米.
故选:B.
【考点】相似三角形的应用
【分析】油面和桶底是一组平行线,可构成相似三角形,画出图形,利用对应边成比例进行解答.此题利用了相似三角形的对应边成比例求解.
解:如图在矩形中,∠C= ,BE=0.8,AB=1,AC=0.8, 由题意知,DE∥BC ,
∴∠AED=∠ABC , ∠ADE=∠C ,
∴△ADE∽△ACB ,
∴ ,
∴
即
解得,CD=0.64m.
故选:B.
【考点】相似三角形的应用.
【分析】根据题意得出△ABC∽△EDC,进而利用相似三角形的性质得出答案.
解:由题意可得:AB=1.5m,BC=0.5m,DC=4m,
△ABC∽△EDC,
则=,
即=,
解得:DE=12,
故选:B.
【考点】相似三角形的应用
【分析】由已知条件△ADE∽△ABC , 得相似三角形对应边成比例,代入数据进行解答.此题是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出梯子AB的长.
解:∵△ADE∽△ABC , ∴AD:AB=DE:BC ,
∴(AB-0.5):AB=1.2:1.4,
∴AB=3.5m.
∴梯子AB的长为3.5m.
故选:A.
【考点】轴对称﹣最短路线问题;角平分线的性质.
【分析】依据勾股定理可求得AB的长,然后在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E,先证明C′E=CE,然后可得到CE+EF=C′E+EF,然后依据垂直线段最短可知当点C′F⊥AC时,CE+EF有最小值,最后利用相似三角形的性质求解即可.
解:如图所示:在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E.
在Rt△ABC中,依据勾股定理可知BA=10.
∵AC=AC′,∠CAD=∠C′AD,AE=C′E,
∴△AEC≌△AEC′.
∴CE=EC′.
∴CE+EF=C′E+EF.
∴当C′F⊥AC时,CE+EF有最小值.
∵C′F⊥AC,BC⊥AC,
∴C′F∥BC.
∴△AFC′∽△ACB.
∴=,即=,解得FC′=.
故选:C.
二 、填空题
【考点】相似三角形的应用
【分析】先根据PO∥AB得到ABC∽△POC , 再利用相似三角形的对应边的比相等得到比例式,代入求解.
解:由题意得PO∥AB ,
∴∠POC=∠ABC , ∠OPC=∠BAC
∴△ABC∽△POC
∴
即:
解得:PO=4.8米.
∴路灯到地面的距离为4.8米.
故答案为:4.8米.
【考点】相似三角形的应用
【分析】因为光是沿直线传播的,所以BD∥AE , 得出△CBD∽△CAE , 再根据相似三角形的对应边成比例列方程求解.
解:∵光是沿直线传播的,
∴BD∥AE ,
∴△CBD∽△CAE ,
∴ ,
即 ,
解得BC=1.5m.
故答案为:1.5.
11.【考点】 相似三角形的应用.
【分析】根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
解:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则,即,
解得:AB=5.6米.
故答案为:5.6.
【考点】相似三角形的应用.
【分析】根据相似三角形的判定推出△ABE∽△ACD,得出比例式,代入求出即可.
解:如图:
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴△ABE∽△ACD,
∴=,
∴=,
解得:CD=18.
故答案为:18.
【考点】相似三角形的应用
【分析】由题意知三角尺与其影子相似,它们的面积比就等于相似比的平方计算即可.此题考查相似三角形的应用,注意相似三角形的面积比就等于相似比的平方.
解:∵三角尺与其影子相似,
∴这个三角尺的面积与它在墙上所形成影子图形的面积之比是 ,
故答案为:4:25.
【考点】相似三角形的应用
【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.
解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故答案为:100.
【点评】此题主要考查了相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.
考点: 相似三角形的判定与性质;待定系数法求反比例函数解析式.
分析: 过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,可证明△AOC∽△OBD,由点A在y=上,可求得△AOC的面积,由相似三角形的性质可求得△BOD的面积,可求得答案.
解答: 解:如图,过A作AC⊥x轴,过B作BD⊥x轴,垂足分别为C、D,
∵∠AOB=90°,
∴∠BOD+∠AOC=∠DBO+∠BOD,
∴∠DBO=∠AOC,
∴△AOC∽△OBD,
∴=()2=()2=,
设A点坐标为(xA,yA),
∵点A在函数y=的图象上,
∴xAyA=1,
∴S△AOC=xAyA=,
∴S△OBD=5S△AOC=,
设B点坐标为(xB,yB),
∴xByB=,
∴xByB=5,
∴过B点的反比例函数的解析式为y=,
故答案为:y=.
点评: 本题主要考查相似三角形的判定和性质,根据条件求得△OBD的面积是解题的关键,注意反比例函数解析式的三种形式的灵活运用,即xy=k,yx﹣1=1,y=.
三 、解答题
【考点】相似三角形的应用
【分析】此题考查了相似三角形的判定与性质的实际应用,解题的关键是将实际问题转化为数学问题解答.相似三角形对应边成比例;对应边成比例且夹角相等的三角形相似.
解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB , ∴△COD∽△BOA .
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
【考点】相似三角形的应用.
【分析】根据镜面反射原理结合相似三角形的判定方法得出△ABC∽△EDC,△ABF∽△GFH,进而利用相似三角形的性质得出AB的长.
【解答】解:由题意可得:∠ABC=∠EDC=∠GFH=90°,
∠ACB=∠ECD,∠AFB=∠GHF,
故△ABC∽△EDC,△ABF∽△GFH,
则=, =,
即=, =,
解得:AB=99,
答:“望月阁”的高AB的长度为99m.
【分析】过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.
解:作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G,可得矩形BDFG.
由题意得:=
∴DF==16(m);
∵GF=BD=CD=5(m),
同理可得:=,
∴AG=1.6×5=8(m),
∴AB=16+8=24(m).
∴铁塔的高度为24m.
【分析】(1)根据题意,构造直角△ABH与△AFG,利用相似三角形对应边的比相等得到结论即可;
(2)将a的值代入函数关系式从而得到函数的关系式,然后根据函数值的取值范围得到不等式组解得自变量的取值范围即可.
解:(1)如图,根据题意得△ABH与△AFG,
得:=,
即:=,
整理得:y=x+200;
(2)当245(cm)≤y<255(cm)得:
,
解得:135≤x<165.
故该男生弹跳时站的位置x的范围是:135(cm)≤x<165(cm).
【考点】相似三角形的应用
【解析】【分析】先由已知条件得△QAB∽△QCD , 列出比例式 ,同理可得 ,根据CD=EF , 把相关数值代入可得小明距离路灯多远;第二题根据第一题得到的比例式及数值,计算可得路灯高度.
(1)解:设DB=xm,
∵AB∥CD ,
∴∠QBA=∠QDC , ∠QAB=∠QCD ,
∴△QAB∽△QCD
∴
同理可得
∵CD=EF
∴
∴
∴x=12
即小明距离路灯12m .
(2)由 得
∴CD=6
即路灯高6m.
【分析】(1)设出边长为xcm,由正方形的性质得出,EH∥AD,EF∥BC,根据平行线的性质,可以得出比例关系式,=、=,代入数据求解即可,
(2)设AK=x,则EH=16-x,再根据=得出EF的表达式,根据矩形面积公式即可得出y与x的函数解析式,
(3)对二次函数表达式进行配方即可求最值.
解:(1)设边长为xcm,
∵矩形为正方形,
∴EH∥AD,EF∥BC,
根据平行线的性质可以得出:=、=,
由题意知EH=x,AD=24,BC=16,EF=x,即 =,=,
∵BE+AE=AB,
∴+=+=1,
解得x=,
∴AK=,
∴当 时,矩形EFGH为正方形;
(2)设AK=x,EH=24-x,
∵EHGF为矩形,
∴=,即EF=x,
∴SEFGH=y=x (24-x)=-x2+16x(0<x<24);
(3)y=-x2+16x
配方得:y=(x-12)2+96,
∴当x=12时,SEFGH有最大值96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.5 综合与实践 测量与误差同步作业
姓名:__________班级:__________考号:__________
一 、选择题
如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)
A、4 B、5 C、6 D、8
数学兴趣小组的小明想测量教学楼前的一棵树的高度.下午课外活动时他测得一根长为1m的竹竿的影长是0.8m.但当他马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图).他先测得留在墙壁上的树影高为1.2m,又测得地面的影长为2.6m,请你帮他算一下,下列哪个数字最接近树高( )m.
A、3.04 B、4.45 C、4.75 D、3.8
如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
A、3倍 B、不知AB的长度,无法计算 C、 D、
小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O, 准星A, 目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到 ,若OA=0.2米,OB=40米, =0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为( )
A、3米 B、0.3米 C、0.03米 D、0.2米
一个油桶高0.8m , 桶内有油,一根长lm的木棒从桶盖小口插入桶内,一端到达桶底,另一端恰好在小口处,抽出木棒量得浸油部分长0.8m,则油桶内的油的高度是( )
A、0.8m B、0.64m C、1m D、0.7m
为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A.10m B.12m C.12.4m D.12.32m
如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC, 则梯子的长为( )
A、3.5m B、3.85m C、4m D、4.2m
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A. B. C. D.6
二、填空题
如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE , 已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=________m.
为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 米.
如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是 米.
如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm, =50cm,则这个三角尺的面积与它在墙上所形成影子图形的面积之比是________。
如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB= m.
如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且=.若点A在y=的图象上,则经过点B的反比例函数的解析式是y= .
三、解答题
如图,零件的外径为16cm, 要求它的壁厚x, 需要先求出内径AB, 现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,CD=5cm,你能求零件的壁厚x吗?
某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=10m,塔影长DE=20m,小惠和小岚的身高都是1.60m,同一时刻,小惠站在点E处,影子在坡面上,小岚站在平地上,影子也在平地上,两人的影长分别是2m和1m,试求塔高AB.
如图所示,竖杆AC、BD的长度分别为200cm、300cm,CD=300cm.现有一男生站在斜杆AB下方的点E处,设CE=x(cm),从E处跳起的摸高EF=y(cm).
(1)求y与x之间的函数关系式;
(2)若245(cm)≤y<255(cm)时,求该男生跳起时站的位置x(cm)的范围.
小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
如图,△ABC是一锐角三角形余料,边BC=16cm,高AD=24cm,要加工成矩形零件,使矩形的一边在BC上,其余两个顶点E、F分别在AB、AC上.
求:(1)AK为何值时,矩形EFGH是正方形?
(2)若设AK=x,SEFGH=y,试写出y与x的函数解析式.
(3)x为何值时,SEFGH达到最大值.
答案解析
一 、选择题
【考点】相似三角形的应用
【分析】由题意得出,△ABC∽△ADE , 利用对应边成比例列方程代入相应数数据求解.
解:如图,由图可知,
∵BC∥ED ,
∴△ABC∽△ADE ,
∴ ,
又DE=10米,AF=3,FG=2米,
∴AG=AF+FG=5米
即 ,
解得BC=6米
故选:C.
【考点】相似三角形的应用
【分析】此题先求出这棵树全落在地面上时的影子的长,再根据在同一时刻物高与影长对应成比例列出方程,解方程求出这棵树的高度.
解:∵留在墙壁上的树影高为1.2m,∴这段影子在地面上的长为:1.2×0.8=0.96(m),
∴这棵树全落在地面上时的影子的长为:2.6+0.96=3.56(m),
∴设这棵树的高度为xm,则 ,解得x=3.56÷0.8=4.45,
∴设这棵树的高度为4.45m.
故选:B.
【考点】相似三角形的应用
【分析】由AB∥A′B′可知,△OAB∽△OA′B′,根据相似三角形的相似比等于对应边上高的比,列方程求解.
解:如图,作OM⊥AB , ON⊥ , ∵AB∥ ,
∴△OAB∽△ ,
∴ ,
即 ,
∴ = AB .
故选:C.
【考点】相似三角形的应用
【分析】由题意可知,准星和靶是平行的,把实际问题抽象到相似三角形中,根据两三角形相似的对应边成比例列出方程,通过解方程可求出偏离的距离.
解:∵ ∥ ∴OA:OB= :
∴
解得: =0.3米.
故选:B.
【考点】相似三角形的应用
【分析】油面和桶底是一组平行线,可构成相似三角形,画出图形,利用对应边成比例进行解答.此题利用了相似三角形的对应边成比例求解.
解:如图在矩形中,∠C= ,BE=0.8,AB=1,AC=0.8, 由题意知,DE∥BC ,
∴∠AED=∠ABC , ∠ADE=∠C ,
∴△ADE∽△ACB ,
∴ ,
∴
即
解得,CD=0.64m.
故选:B.
【考点】相似三角形的应用.
【分析】根据题意得出△ABC∽△EDC,进而利用相似三角形的性质得出答案.
解:由题意可得:AB=1.5m,BC=0.5m,DC=4m,
△ABC∽△EDC,
则=,
即=,
解得:DE=12,
故选:B.
【考点】相似三角形的应用
【分析】由已知条件△ADE∽△ABC , 得相似三角形对应边成比例,代入数据进行解答.此题是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出梯子AB的长.
解:∵△ADE∽△ABC , ∴AD:AB=DE:BC ,
∴(AB-0.5):AB=1.2:1.4,
∴AB=3.5m.
∴梯子AB的长为3.5m.
故选:A.
【考点】轴对称﹣最短路线问题;角平分线的性质.
【分析】依据勾股定理可求得AB的长,然后在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E,先证明C′E=CE,然后可得到CE+EF=C′E+EF,然后依据垂直线段最短可知当点C′F⊥AC时,CE+EF有最小值,最后利用相似三角形的性质求解即可.
解:如图所示:在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E.
在Rt△ABC中,依据勾股定理可知BA=10.
∵AC=AC′,∠CAD=∠C′AD,AE=C′E,
∴△AEC≌△AEC′.
∴CE=EC′.
∴CE+EF=C′E+EF.
∴当C′F⊥AC时,CE+EF有最小值.
∵C′F⊥AC,BC⊥AC,
∴C′F∥BC.
∴△AFC′∽△ACB.
∴=,即=,解得FC′=.
故选:C.
二 、填空题
【考点】相似三角形的应用
【分析】先根据PO∥AB得到ABC∽△POC , 再利用相似三角形的对应边的比相等得到比例式,代入求解.
解:由题意得PO∥AB ,
∴∠POC=∠ABC , ∠OPC=∠BAC
∴△ABC∽△POC
∴
即:
解得:PO=4.8米.
∴路灯到地面的距离为4.8米.
故答案为:4.8米.
【考点】相似三角形的应用
【分析】因为光是沿直线传播的,所以BD∥AE , 得出△CBD∽△CAE , 再根据相似三角形的对应边成比例列方程求解.
解:∵光是沿直线传播的,
∴BD∥AE ,
∴△CBD∽△CAE ,
∴ ,
即 ,
解得BC=1.5m.
故答案为:1.5.
11.【考点】 相似三角形的应用.
【分析】根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
解:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则,即,
解得:AB=5.6米.
故答案为:5.6.
【考点】相似三角形的应用.
【分析】根据相似三角形的判定推出△ABE∽△ACD,得出比例式,代入求出即可.
解:如图:
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴△ABE∽△ACD,
∴=,
∴=,
解得:CD=18.
故答案为:18.
【考点】相似三角形的应用
【分析】由题意知三角尺与其影子相似,它们的面积比就等于相似比的平方计算即可.此题考查相似三角形的应用,注意相似三角形的面积比就等于相似比的平方.
解:∵三角尺与其影子相似,
∴这个三角尺的面积与它在墙上所形成影子图形的面积之比是 ,
故答案为:4:25.
【考点】相似三角形的应用
【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例可得两岸间的大致距离AB.
解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得:AB=(米).
故答案为:100.
【点评】此题主要考查了相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.
考点: 相似三角形的判定与性质;待定系数法求反比例函数解析式.
分析: 过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,可证明△AOC∽△OBD,由点A在y=上,可求得△AOC的面积,由相似三角形的性质可求得△BOD的面积,可求得答案.
解答: 解:如图,过A作AC⊥x轴,过B作BD⊥x轴,垂足分别为C、D,
∵∠AOB=90°,
∴∠BOD+∠AOC=∠DBO+∠BOD,
∴∠DBO=∠AOC,
∴△AOC∽△OBD,
∴=()2=()2=,
设A点坐标为(xA,yA),
∵点A在函数y=的图象上,
∴xAyA=1,
∴S△AOC=xAyA=,
∴S△OBD=5S△AOC=,
设B点坐标为(xB,yB),
∴xByB=,
∴xByB=5,
∴过B点的反比例函数的解析式为y=,
故答案为:y=.
点评: 本题主要考查相似三角形的判定和性质,根据条件求得△OBD的面积是解题的关键,注意反比例函数解析式的三种形式的灵活运用,即xy=k,yx﹣1=1,y=.
三 、解答题
【考点】相似三角形的应用
【分析】此题考查了相似三角形的判定与性质的实际应用,解题的关键是将实际问题转化为数学问题解答.相似三角形对应边成比例;对应边成比例且夹角相等的三角形相似.
解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB , ∴△COD∽△BOA .
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
【考点】相似三角形的应用.
【分析】根据镜面反射原理结合相似三角形的判定方法得出△ABC∽△EDC,△ABF∽△GFH,进而利用相似三角形的性质得出AB的长.
【解答】解:由题意可得:∠ABC=∠EDC=∠GFH=90°,
∠ACB=∠ECD,∠AFB=∠GHF,
故△ABC∽△EDC,△ABF∽△GFH,
则=, =,
即=, =,
解得:AB=99,
答:“望月阁”的高AB的长度为99m.
【分析】过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.
解:作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G,可得矩形BDFG.
由题意得:=
∴DF==16(m);
∵GF=BD=CD=5(m),
同理可得:=,
∴AG=1.6×5=8(m),
∴AB=16+8=24(m).
∴铁塔的高度为24m.
【分析】(1)根据题意,构造直角△ABH与△AFG,利用相似三角形对应边的比相等得到结论即可;
(2)将a的值代入函数关系式从而得到函数的关系式,然后根据函数值的取值范围得到不等式组解得自变量的取值范围即可.
解:(1)如图,根据题意得△ABH与△AFG,
得:=,
即:=,
整理得:y=x+200;
(2)当245(cm)≤y<255(cm)得:
,
解得:135≤x<165.
故该男生弹跳时站的位置x的范围是:135(cm)≤x<165(cm).
【考点】相似三角形的应用
【解析】【分析】先由已知条件得△QAB∽△QCD , 列出比例式 ,同理可得 ,根据CD=EF , 把相关数值代入可得小明距离路灯多远;第二题根据第一题得到的比例式及数值,计算可得路灯高度.
(1)解:设DB=xm,
∵AB∥CD ,
∴∠QBA=∠QDC , ∠QAB=∠QCD ,
∴△QAB∽△QCD
∴
同理可得
∵CD=EF
∴
∴
∴x=12
即小明距离路灯12m .
(2)由 得
∴CD=6
即路灯高6m.
【分析】(1)设出边长为xcm,由正方形的性质得出,EH∥AD,EF∥BC,根据平行线的性质,可以得出比例关系式,=、=,代入数据求解即可,
(2)设AK=x,则EH=16-x,再根据=得出EF的表达式,根据矩形面积公式即可得出y与x的函数解析式,
(3)对二次函数表达式进行配方即可求最值.
解:(1)设边长为xcm,
∵矩形为正方形,
∴EH∥AD,EF∥BC,
根据平行线的性质可以得出:=、=,
由题意知EH=x,AD=24,BC=16,EF=x,即 =,=,
∵BE+AE=AB,
∴+=+=1,
解得x=,
∴AK=,
∴当 时,矩形EFGH为正方形;
(2)设AK=x,EH=24-x,
∵EHGF为矩形,
∴=,即EF=x,
∴SEFGH=y=x (24-x)=-x2+16x(0<x<24);
(3)y=-x2+16x
配方得:y=(x-12)2+96,
∴当x=12时,SEFGH有最大值96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
