2018年秋人教版九年级上《24.3正多边形和圆》课时练(含答案解析)
文档属性
| 名称 | 2018年秋人教版九年级上《24.3正多边形和圆》课时练(含答案解析) | 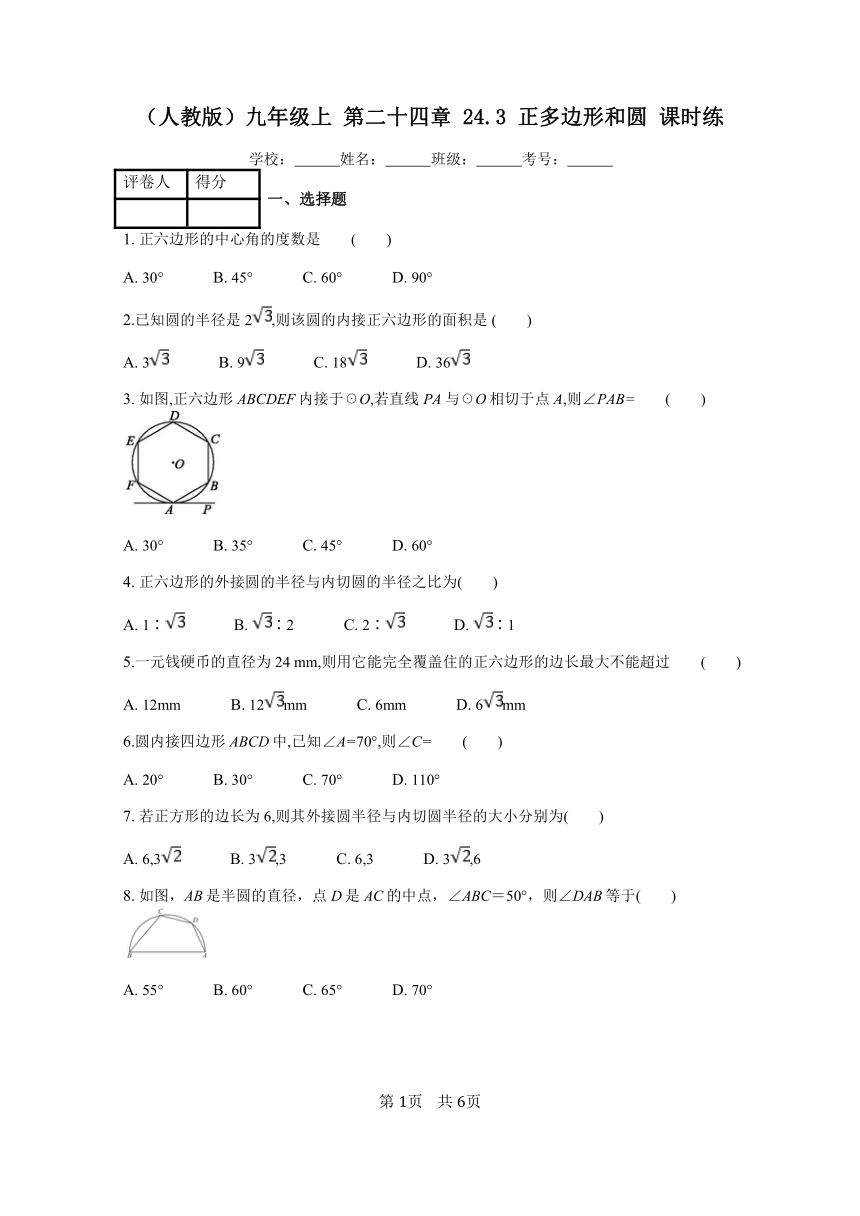 | |
| 格式 | zip | ||
| 文件大小 | 266.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-08 21:41:44 | ||
图片预览

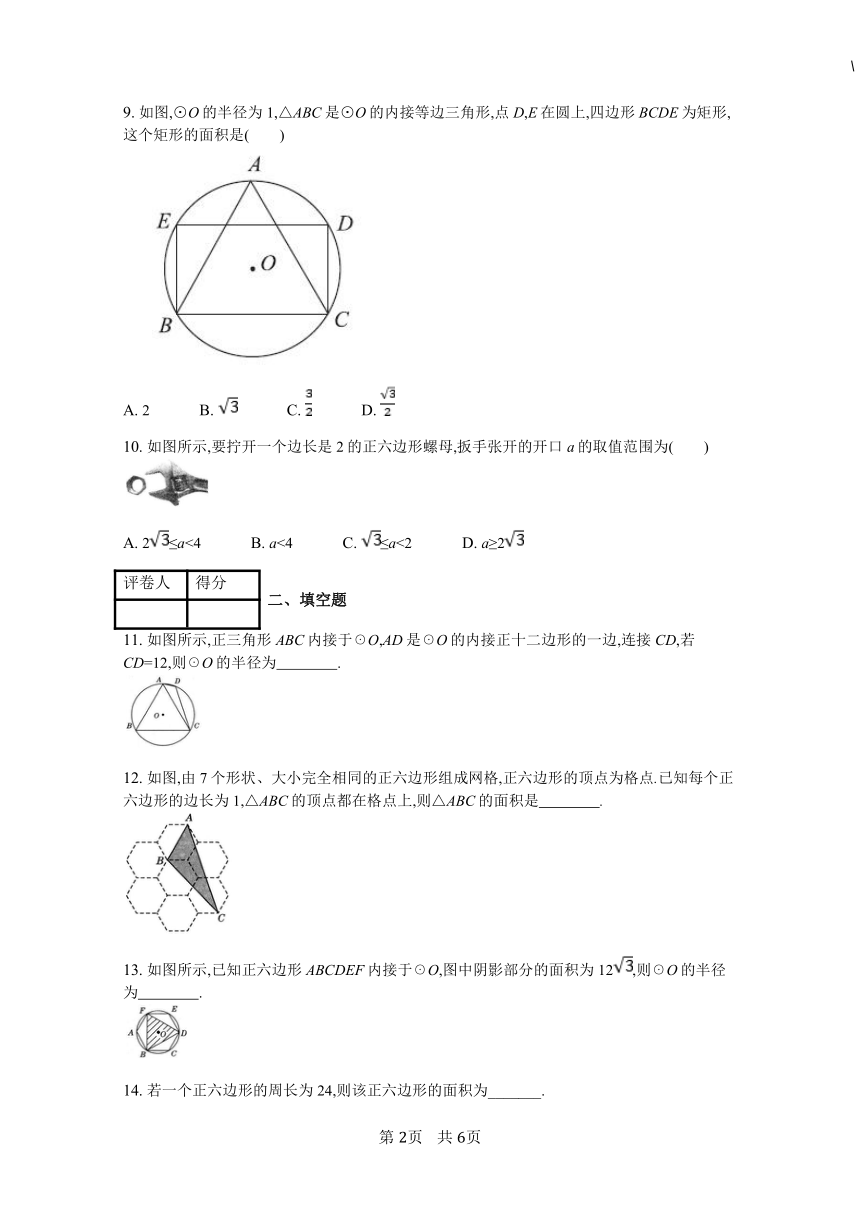
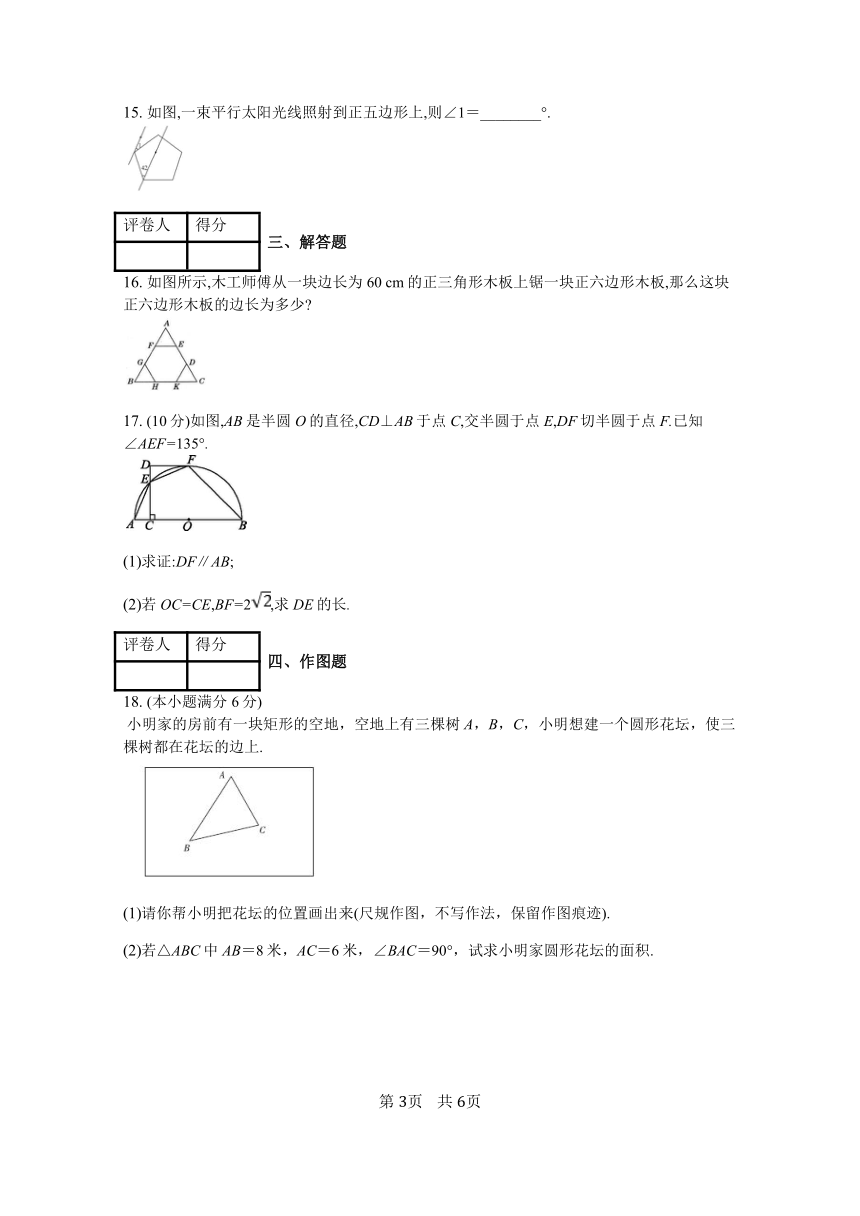
文档简介
(人教版)九年级上 第二十四章 24.3 正多边形和圆 课时练
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人
得分
一、选择题
1. 正六边形的中心角的度数是 ( )
A. 30°?????????????B. 45°?????????????C. 60°?????????????D. 90°?????????????
2.已知圆的半径是2,则该圆的内接正六边形的面积是?( )
A. 3?????????????B. 9?????????????C. 18?????????????D. 36?????????????
3. 如图,正六边形ABCDEF内接于☉O,若直线PA与☉O相切于点A,则∠PAB= ( ) ?
A. 30°?????????????B. 35°?????????????C. 45°?????????????D. 60°?????????????
4. 正六边形的外接圆的半径与内切圆的半径之比为( )
A. 1∶?????????????B. ∶2?????????????C. 2∶?????????????D. ∶1?????????????
5.一元钱硬币的直径为24?mm,则用它能完全覆盖住的正六边形的边长最大不能超过 ( )
A. 12mm?????????????B. 12mm?????????????C. 6mm?????????????D. 6mm?????????????
6.圆内接四边形ABCD中,已知∠A=70°,则∠C= ( )
A. 20°?????????????B. 30°?????????????C. 70°?????????????D. 110°?????????????
7. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A. 6,3?????????????B. 3,3?????????????C. 6,3?????????????D. 3,6?????????????
8. 如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等于( ) ?
A. 55°?????????????B. 60°?????????????C. 65°?????????????D. 70°?????????????
9. 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( ) ?
A. 2?????????????B. ?????????????C. ?????????????D. ?????????????
10. 如图所示,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值范围为( ) ?
A. 2≤a<4?????????????B. a<4?????????????C. ≤a<2?????????????D. a≥2?????????????
评卷人
得分
二、填空题
11. 如图所示,正三角形ABC内接于☉O,AD是☉O的内接正十二边形的一边,连接CD,若CD=12,则☉O的半径为 . ?
12. 如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是 . ?
13. 如图所示,已知正六边形ABCDEF内接于☉O,图中阴影部分的面积为12,则☉O的半径为 . ?
14. 若一个正六边形的周长为24,则该正六边形的面积为_______.
15. 如图,一束平行太阳光线照射到正五边形上,则∠1=________°. ?
评卷人
得分
三、解答题
16. 如图所示,木工师傅从一块边长为60?cm的正三角形木板上锯一块正六边形木板,那么这块正六边形木板的边长为多少? ?
17.?(10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°. ?
(1)求证:DF∥AB;
(2)若OC=CE,BF=2,求DE的长.
评卷人
得分
四、作图题
18. (本小题满分6分) ?小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上. ?
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若△ABC中AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
参考答案
1. 【答案】C【解析】有6个中心角平分360度,所以正六边形的中心角为=60°.
2. 【答案】C【解析】本题考查正多边形和圆,难度中等偏上.正六边形被圆的半径分成六个全等的等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,∴正六边形的面积=18.答案是C.
3. 【答案】A【解析】本题考查正多边形和圆、切线的性质,难度中等.连接OA,根据直线PA为切线可得∠OAP=90°,根据正六边形的性质可得∠OAB=60°,则∠PAB=∠OAP-∠OAB=90°-60°=30°.答案是A.
4. 【答案】C【解析】设正六边形的外接圆的半径为r,根据内切圆的半径是正六边形的边心距,得内切圆的半径为r.则正六边形的外接圆的半径与内切圆的半径之比为2∶.故选C.
5. 【答案】A【解析】本题考查圆内接多边形问题,难度中等.根据圆内接正六边形的性质得出其边长等于圆的半径即可,故选A.
6. 【答案】D【解析】本题考查圆内接四边形的性质,难度中等偏下.因为四边形ABCD是圆内接四边形,所以∠A+∠C=180°.因为∠A=70°,所以∠C=180°-70°=110°.答案是D.
7. 【答案】B【解析】如图,?OA,?OE分别为正方形的外接圆半径和内接圆半径,?若正方形的边长为6,则对角线长为6,?∴OA=3.由垂径定理得OE=AE=3.故选B. ?
8. 【答案】C【解析】由题意可知,AD弧的度数=50°,所以BCD弧的度数=180°-50°=130°,而∠DAB=BCD弧的度数的一半=65°,故选C.
9. 【答案】B【解析】连接BD,OC,∵四边形BCDE为矩形,∴∠BCD=90°,∴BD为⊙O的直径,∴BD=2.∵△ABC为等边三角形,∴∠A=60°,∴∠BOC=2∠A=120°.而OB=OC,∴∠CBD=30°.在Rt△BCD中,CD=BD=1,BC=CD=,∴矩形BCDE的面积=BC·CD=.故选B.
10. 【答案】A【解析】如图,?连接AD,BD,?正六边形ABCDEF的边长为2.根据正六边形的性质,得AD=4,∠ABD=90°,由勾股定理得BD=2.要拧开正六边形螺母,扳手张开的开口a大于等于BD,且小于AD,即2≤a<4.故选A. ?
11. 【答案】6 12. 【答案】2 13. 【答案】4 14. 【答案】24 15. 【答案】30 16.
17. 【答案】由题意知,RF=FG=GH.明显EF平行于BC,角A等于60度,则三角形AFE是正三角形.EF=AF,同理BG=GH=FG.所以G,F是AB边的三等分点.所以正六边形的边长为20cm. ?
18.
(1) 【答案】连接OF, ?∵DF切半圆O于点F,∴DF⊥OF. ?∵∠AEF=135°,四边形ABFE为圆内接四边形, ?∴∠B=45°. ? ?∴∠FOB=90°, ?∴AB⊥OF, ?又CD⊥AB,DF切半圆O于点F, ?∴四边形DFOC为矩形, ?∴DF∥AB. ?(2) 【答案】连接OE, ?∵BF=2,∠FOB=90°, ?∴OB=OF=2. ?∵OC=CE,CE⊥AB,OE=OF=2, ?∴CE=. ?∵DC∥OF,DF∥AB,∴DC=OF=2. ?∴DE=DC-CE=2-. ?
19.
(1) 【答案】用尺规作出两边的垂直平分线(2分) ?作出圆(3分) ?⊙O即为所求作的花园的位置 ?(2) 【答案】∵∠BAC=90°,AB=8米,AC=6米, ?∴BC=10米 ?∴△ABC外接圆的半径为5米(5分) ?∴小明家圆形花坛的面积为25π平方米.(6分) ?
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人
得分
一、选择题
1. 正六边形的中心角的度数是 ( )
A. 30°?????????????B. 45°?????????????C. 60°?????????????D. 90°?????????????
2.已知圆的半径是2,则该圆的内接正六边形的面积是?( )
A. 3?????????????B. 9?????????????C. 18?????????????D. 36?????????????
3. 如图,正六边形ABCDEF内接于☉O,若直线PA与☉O相切于点A,则∠PAB= ( ) ?
A. 30°?????????????B. 35°?????????????C. 45°?????????????D. 60°?????????????
4. 正六边形的外接圆的半径与内切圆的半径之比为( )
A. 1∶?????????????B. ∶2?????????????C. 2∶?????????????D. ∶1?????????????
5.一元钱硬币的直径为24?mm,则用它能完全覆盖住的正六边形的边长最大不能超过 ( )
A. 12mm?????????????B. 12mm?????????????C. 6mm?????????????D. 6mm?????????????
6.圆内接四边形ABCD中,已知∠A=70°,则∠C= ( )
A. 20°?????????????B. 30°?????????????C. 70°?????????????D. 110°?????????????
7. 若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A. 6,3?????????????B. 3,3?????????????C. 6,3?????????????D. 3,6?????????????
8. 如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等于( ) ?
A. 55°?????????????B. 60°?????????????C. 65°?????????????D. 70°?????????????
9. 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( ) ?
A. 2?????????????B. ?????????????C. ?????????????D. ?????????????
10. 如图所示,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值范围为( ) ?
A. 2≤a<4?????????????B. a<4?????????????C. ≤a<2?????????????D. a≥2?????????????
评卷人
得分
二、填空题
11. 如图所示,正三角形ABC内接于☉O,AD是☉O的内接正十二边形的一边,连接CD,若CD=12,则☉O的半径为 . ?
12. 如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是 . ?
13. 如图所示,已知正六边形ABCDEF内接于☉O,图中阴影部分的面积为12,则☉O的半径为 . ?
14. 若一个正六边形的周长为24,则该正六边形的面积为_______.
15. 如图,一束平行太阳光线照射到正五边形上,则∠1=________°. ?
评卷人
得分
三、解答题
16. 如图所示,木工师傅从一块边长为60?cm的正三角形木板上锯一块正六边形木板,那么这块正六边形木板的边长为多少? ?
17.?(10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°. ?
(1)求证:DF∥AB;
(2)若OC=CE,BF=2,求DE的长.
评卷人
得分
四、作图题
18. (本小题满分6分) ?小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上. ?
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若△ABC中AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
参考答案
1. 【答案】C【解析】有6个中心角平分360度,所以正六边形的中心角为=60°.
2. 【答案】C【解析】本题考查正多边形和圆,难度中等偏上.正六边形被圆的半径分成六个全等的等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,∴正六边形的面积=18.答案是C.
3. 【答案】A【解析】本题考查正多边形和圆、切线的性质,难度中等.连接OA,根据直线PA为切线可得∠OAP=90°,根据正六边形的性质可得∠OAB=60°,则∠PAB=∠OAP-∠OAB=90°-60°=30°.答案是A.
4. 【答案】C【解析】设正六边形的外接圆的半径为r,根据内切圆的半径是正六边形的边心距,得内切圆的半径为r.则正六边形的外接圆的半径与内切圆的半径之比为2∶.故选C.
5. 【答案】A【解析】本题考查圆内接多边形问题,难度中等.根据圆内接正六边形的性质得出其边长等于圆的半径即可,故选A.
6. 【答案】D【解析】本题考查圆内接四边形的性质,难度中等偏下.因为四边形ABCD是圆内接四边形,所以∠A+∠C=180°.因为∠A=70°,所以∠C=180°-70°=110°.答案是D.
7. 【答案】B【解析】如图,?OA,?OE分别为正方形的外接圆半径和内接圆半径,?若正方形的边长为6,则对角线长为6,?∴OA=3.由垂径定理得OE=AE=3.故选B. ?
8. 【答案】C【解析】由题意可知,AD弧的度数=50°,所以BCD弧的度数=180°-50°=130°,而∠DAB=BCD弧的度数的一半=65°,故选C.
9. 【答案】B【解析】连接BD,OC,∵四边形BCDE为矩形,∴∠BCD=90°,∴BD为⊙O的直径,∴BD=2.∵△ABC为等边三角形,∴∠A=60°,∴∠BOC=2∠A=120°.而OB=OC,∴∠CBD=30°.在Rt△BCD中,CD=BD=1,BC=CD=,∴矩形BCDE的面积=BC·CD=.故选B.
10. 【答案】A【解析】如图,?连接AD,BD,?正六边形ABCDEF的边长为2.根据正六边形的性质,得AD=4,∠ABD=90°,由勾股定理得BD=2.要拧开正六边形螺母,扳手张开的开口a大于等于BD,且小于AD,即2≤a<4.故选A. ?
11. 【答案】6 12. 【答案】2 13. 【答案】4 14. 【答案】24 15. 【答案】30 16.
17. 【答案】由题意知,RF=FG=GH.明显EF平行于BC,角A等于60度,则三角形AFE是正三角形.EF=AF,同理BG=GH=FG.所以G,F是AB边的三等分点.所以正六边形的边长为20cm. ?
18.
(1) 【答案】连接OF, ?∵DF切半圆O于点F,∴DF⊥OF. ?∵∠AEF=135°,四边形ABFE为圆内接四边形, ?∴∠B=45°. ? ?∴∠FOB=90°, ?∴AB⊥OF, ?又CD⊥AB,DF切半圆O于点F, ?∴四边形DFOC为矩形, ?∴DF∥AB. ?(2) 【答案】连接OE, ?∵BF=2,∠FOB=90°, ?∴OB=OF=2. ?∵OC=CE,CE⊥AB,OE=OF=2, ?∴CE=. ?∵DC∥OF,DF∥AB,∴DC=OF=2. ?∴DE=DC-CE=2-. ?
19.
(1) 【答案】用尺规作出两边的垂直平分线(2分) ?作出圆(3分) ?⊙O即为所求作的花园的位置 ?(2) 【答案】∵∠BAC=90°,AB=8米,AC=6米, ?∴BC=10米 ?∴△ABC外接圆的半径为5米(5分) ?∴小明家圆形花坛的面积为25π平方米.(6分) ?
同课章节目录
