2018年秋人教版九年级上《23.2中心对称》课时练含答案
文档属性
| 名称 | 2018年秋人教版九年级上《23.2中心对称》课时练含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-08 00:00:00 | ||
图片预览

文档简介
(人教版)九年级上 第二十三章 23.2 中心对称 课时练
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人
得分
一、选择题
1. 下列图形是中心对称图形的是 ( )
A. ?????????????B. ?????????????C.?????????????D. ?????????????
2. 在同一直角坐标系中,P,Q分别是y=-x+3与y=3x-5的图象上的点,且P,Q关于原点成中心对称,则点P的坐标是( )
A. (2,1)?????????????B. (-2,5)?????????????C. (-,)?????????????D. (-4,7)?????????????
3. 下列图形中,既是轴对称图形又是中心对称图形的是( )?
A. A?????????????B. B?????????????C. C?????????????D. D?????????????
4. 平面直角坐标系中,与点(2,-3)关于原点中心对称的点是( )
A. (-3,2)?????????????B. (3,-2)?????????????C. (-2,3)?????????????D. (2,3)?????????????
5. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( ) ?
A. (-a,-b)?????????????B. (-a,-b-1)?????????????C. (-a,-b+1)?????????????D. (-a,-b+2)?????????????
6. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A. 33?????????????B. -33?????????????C. -7?????????????D. 7?????????????
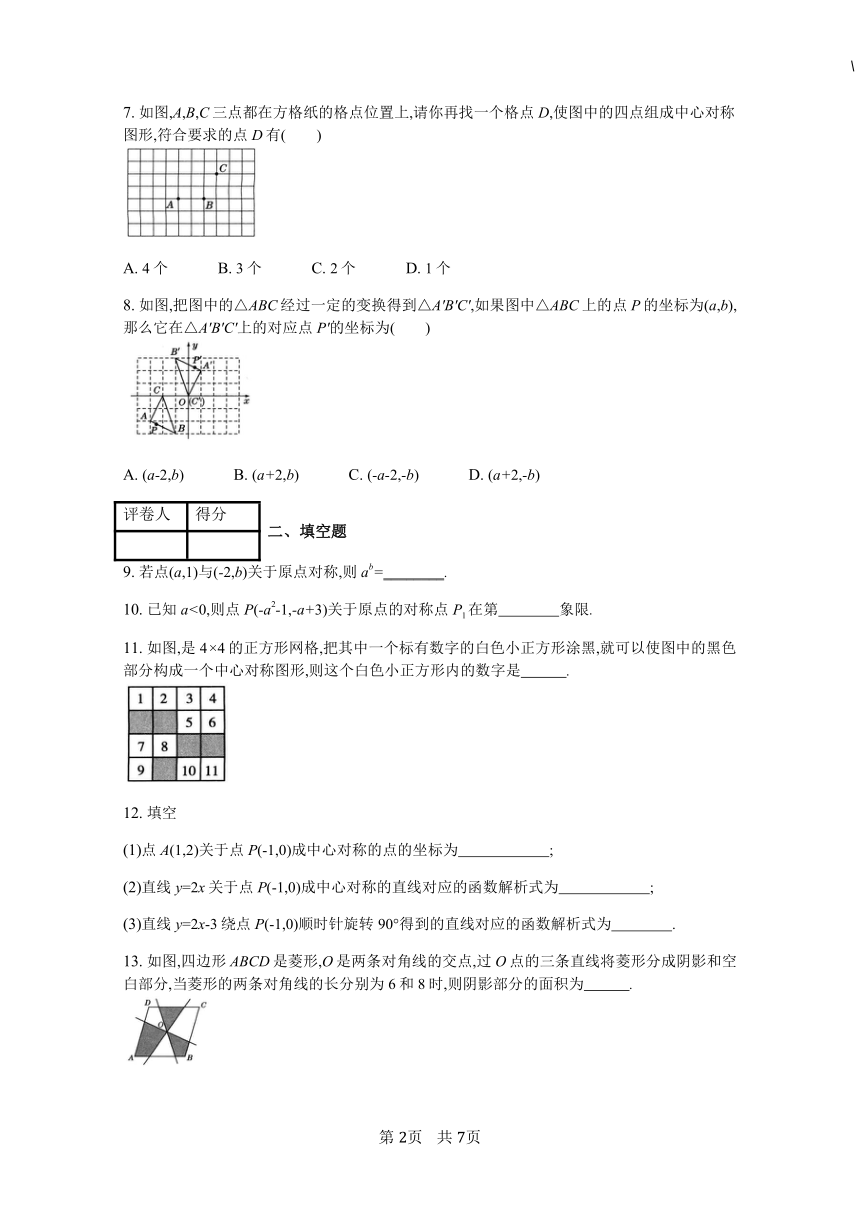
7. 如图,A,B,C三点都在方格纸的格点位置上,请你再找一个格点D,使图中的四点组成中心对称图形,符合要求的点D有( ) ?
A. 4个?????????????B. 3个?????????????C. 2个?????????????D. 1个?????????????
8. 如图,把图中的△ABC经过一定的变换得到△A'B'C',如果图中△ABC上的点P的坐标为(a,b),那么它在△A'B'C'上的对应点P'的坐标为( ) ?
A. (a-2,b)?????????????B. (a+2,b)?????????????C. (-a-2,-b)?????????????D. (a+2,-b)?????????????
评卷人
得分
二、填空题
9. 若点(a,1)与(-2,b)关于原点对称,则ab=________.
10. 已知a<0,则点P(-a2-1,-a+3)关于原点的对称点P1在第 象限.
11. 如图,是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 . ?
12. 填空
(1)点A(1,2)关于点P(-1,0)成中心对称的点的坐标为 ;
(2)直线y=2x关于点P(-1,0)成中心对称的直线对应的函数解析式为 ;
(3)直线y=2x-3绕点P(-1,0)顺时针旋转90°得到的直线对应的函数解析式为 .
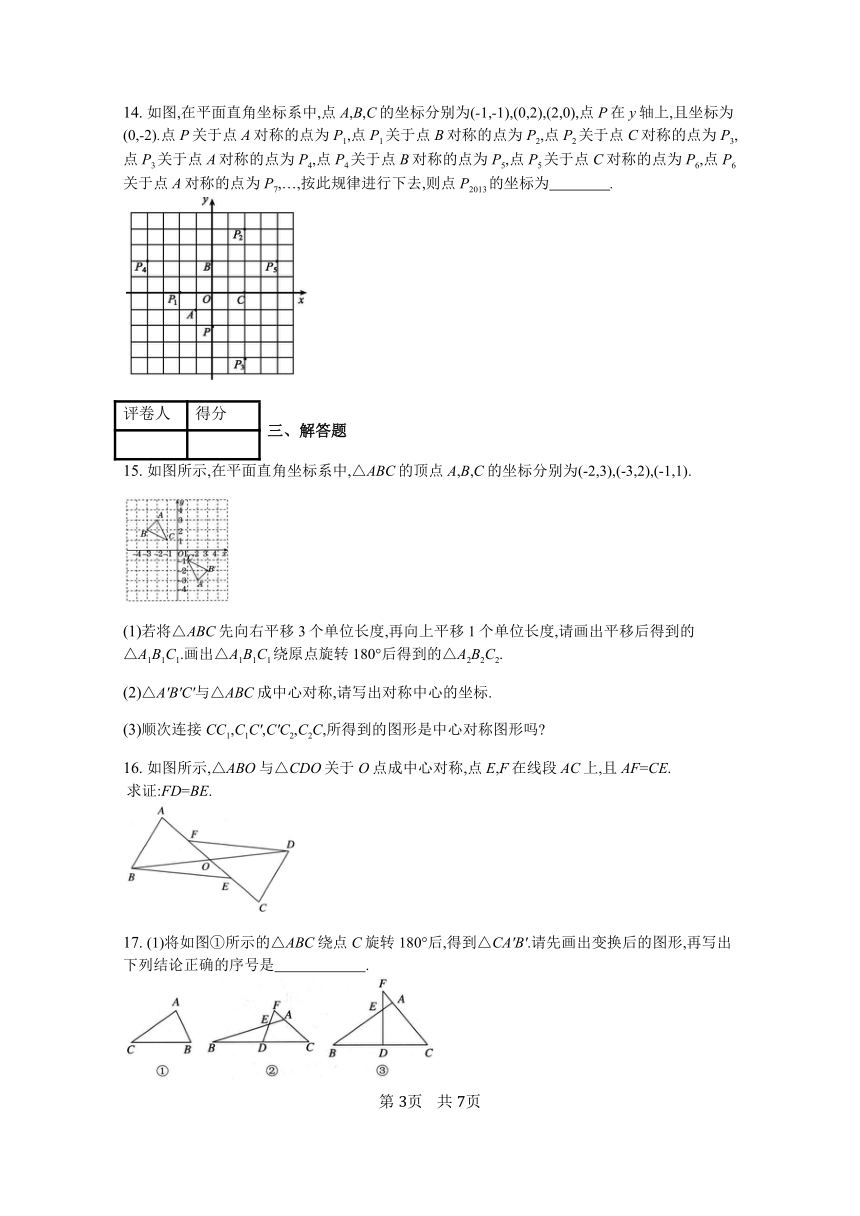
13. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . ?
14. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,-1),(0,2),(2,0),点P在y轴上,且坐标为(0,-2).点P关于点A对称的点为P1,点P1关于点B对称的点为P2,点P2关于点C对称的点为P3,点P3关于点A对称的点为P4,点P4关于点B对称的点为P5,点P5关于点C对称的点为P6,点P6关于点A对称的点为P7,…,按此规律进行下去,则点P2013的坐标为 . ?
评卷人
得分
三、解答题
15. 如图所示,在平面直角坐标系中,△ABC的顶点A,B,C的坐标分别为(-2,3),(-3,2),(-1,1).?
(1)若将△ABC先向右平移3个单位长度,再向上平移1个单位长度,请画出平移后得到的△A1B1C1.画出△A1B1C1绕原点旋转180°后得到的△A2B2C2.
(2)△A'B'C'与△ABC成中心对称,请写出对称中心的坐标.
(3)顺次连接CC1,C1C',C'C2,C2C,所得到的图形是中心对称图形吗?
16. 如图所示,△ABO与△CDO关于O点成中心对称,点E,F在线段AC上,且AF=CE. ?求证:FD=BE. ?
17. (1)将如图①所示的△ABC绕点C旋转180°后,得到△CA'B'.请先画出变换后的图形,再写出下列结论正确的序号是 . ? ?①△ABC≌△A'B'C; ?②线段AB绕C点旋转180°后,得到线段A'B'; ?③A'B'∥AB; ?④C是线段BB'的中点. ?在第1问的启发下解答下面问题: ?(2)如图②,在△ABC中,∠BAC=120°,D是BC的中点,射线DF交BA于E,交CA的延长线于F,请猜想∠F等于多少度时,BE=CF?(直接写出结果,不需证明) ?(3)如图③,在△ABC中,如果∠BAC≠120°,而(2)中的其他条件不变,若BE=CF的结论仍然成立,那么∠BAC与∠F满足什么数量关系(等式表示)?并加以证明.
参考答案
1. 【答案】A【解析】本题考查中心对称图形的识别,难度较小.在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与原图形重合,这样的图形叫作中心对称图形.根据定义可以判定四个选项中,选项B,C,D都不是中心对称图形,只有A选项是中心对称图形,答案为A.
2. 【答案】C【解析】根据题意可设点P的坐标为(a,-a+3),点Q的坐标为(-a,a-3),?∵Q?是y=3x-5图象上的点,∴-3a-5=a-3,?解得a=-,∴点P的坐标为.故选C.
3. 【答案】D【解析】轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.A是轴对称图形,但不是中心对称图形,故本选项错误;B不是轴对称图形,但是中心对称图形,故本选项错误;C是轴对称图形,但不是中心对称图形,故本选项错误;D是轴对称图形,也是中心对称图形,故本选项正确.故选D.
4. 【答案】C【解析】若(x,y)是关于原点对称,则对称点的坐标为(-x,-y), ?∴(2,-3)关于原点中心对称的点是(-2,3),故选C.
5. 【答案】D【解析】∵△ABC绕点C(0,1)旋转180°得到△A'B'C,?∴点A(a,b)与点A'关于点C(0,1)对称,∴点A'的坐标是(-a,-b+2).?故选D.
6. 【答案】D【解析】∵点P(-20,a)与点Q(b,13)关于原点对称,∴a=-13,b=20,∴a+b=7.故选D.
7. 【答案】B【解析】根据中心对称的定义可知,符合要求的点D有3个,如图所示: ?
8. 【答案】C【解析】由题图知,△ABC与△A'B'C'关于点(-1,0)成中心对称,则点P(a,b)与点P'关于点(-1,0)中心对称,∴P'(-a-2,-b).故选C.
9. 【答案】 ?
10. 【答案】四 ?
11. 【答案】3 ?
(1) 【答案】(-3,-2) ?【解析】如图所示,连接AP并延长至点A',使A'P=AP,则点A'的坐标即为所求; ? ?(2) 【答案】y=2x+4 ?【解析】如图所示,任取直线y=2x上的两点,如O(0,0),B(1,2),则它们关于点P(-1,0)成中心对称的点分别为:A'(-2,0),B'(-3,-2),连接A'B',于是可得所求直线A'B'对应的函数解析式为y=2x+4; ? ?(3) 【答案】y=-x-3 ?【解析】如图所示,任取直线y=2x-3上两点,如A(0,-3),B(1,-1),分别将点A,B绕点P(-1,0)顺时针旋转90°得到A'(-4,-1),B'(-2,-2),连接A'B',于是可得所求直线A'B'对应的函数解析式为y=-x-3. ? ?
12. 【答案】12 ?
13. 【答案】(2,-4) ?
(1) 【答案】如图所示. ? ?(2) 【答案】(0,0). ?(3) 【答案】如图,是中心对称图形. ?
14. 【答案】由对称性得到三角形全等.沿着此思路证明如下: ?∵△ABO与△CDO关于O点成中心对称,∴OB=OD,OA=OC, ?∵AF=CE,∴OF=OE, ?在△DOF和△BOE中,∵OB=OD,∠DOF=∠BOE,OF=OE, ?∴△DOF≌△BOE,∴FD=BE. ?
15. 【答案】(1)如图①.①②③④??(2)60°. ?(3)等量关系:∠BAC=2∠F. ?证明如下:作△DBF'与△FCD关于点D成中心对称,如图②, ?则∠F'=∠F,FC=BF'=BE,∴∠F'=∠F=∠BED=∠FEA,∴∠BAC=2∠F. ? ?
学校:????????????姓名:????????????班级:????????????考号:????????????
评卷人
得分
一、选择题
1. 下列图形是中心对称图形的是 ( )
A. ?????????????B. ?????????????C.?????????????D. ?????????????
2. 在同一直角坐标系中,P,Q分别是y=-x+3与y=3x-5的图象上的点,且P,Q关于原点成中心对称,则点P的坐标是( )
A. (2,1)?????????????B. (-2,5)?????????????C. (-,)?????????????D. (-4,7)?????????????
3. 下列图形中,既是轴对称图形又是中心对称图形的是( )?
A. A?????????????B. B?????????????C. C?????????????D. D?????????????
4. 平面直角坐标系中,与点(2,-3)关于原点中心对称的点是( )
A. (-3,2)?????????????B. (3,-2)?????????????C. (-2,3)?????????????D. (2,3)?????????????
5. 如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( ) ?
A. (-a,-b)?????????????B. (-a,-b-1)?????????????C. (-a,-b+1)?????????????D. (-a,-b+2)?????????????
6. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A. 33?????????????B. -33?????????????C. -7?????????????D. 7?????????????
7. 如图,A,B,C三点都在方格纸的格点位置上,请你再找一个格点D,使图中的四点组成中心对称图形,符合要求的点D有( ) ?
A. 4个?????????????B. 3个?????????????C. 2个?????????????D. 1个?????????????
8. 如图,把图中的△ABC经过一定的变换得到△A'B'C',如果图中△ABC上的点P的坐标为(a,b),那么它在△A'B'C'上的对应点P'的坐标为( ) ?
A. (a-2,b)?????????????B. (a+2,b)?????????????C. (-a-2,-b)?????????????D. (a+2,-b)?????????????
评卷人
得分
二、填空题
9. 若点(a,1)与(-2,b)关于原点对称,则ab=________.
10. 已知a<0,则点P(-a2-1,-a+3)关于原点的对称点P1在第 象限.
11. 如图,是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 . ?
12. 填空
(1)点A(1,2)关于点P(-1,0)成中心对称的点的坐标为 ;
(2)直线y=2x关于点P(-1,0)成中心对称的直线对应的函数解析式为 ;
(3)直线y=2x-3绕点P(-1,0)顺时针旋转90°得到的直线对应的函数解析式为 .
13. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . ?
14. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,-1),(0,2),(2,0),点P在y轴上,且坐标为(0,-2).点P关于点A对称的点为P1,点P1关于点B对称的点为P2,点P2关于点C对称的点为P3,点P3关于点A对称的点为P4,点P4关于点B对称的点为P5,点P5关于点C对称的点为P6,点P6关于点A对称的点为P7,…,按此规律进行下去,则点P2013的坐标为 . ?
评卷人
得分
三、解答题
15. 如图所示,在平面直角坐标系中,△ABC的顶点A,B,C的坐标分别为(-2,3),(-3,2),(-1,1).?
(1)若将△ABC先向右平移3个单位长度,再向上平移1个单位长度,请画出平移后得到的△A1B1C1.画出△A1B1C1绕原点旋转180°后得到的△A2B2C2.
(2)△A'B'C'与△ABC成中心对称,请写出对称中心的坐标.
(3)顺次连接CC1,C1C',C'C2,C2C,所得到的图形是中心对称图形吗?
16. 如图所示,△ABO与△CDO关于O点成中心对称,点E,F在线段AC上,且AF=CE. ?求证:FD=BE. ?
17. (1)将如图①所示的△ABC绕点C旋转180°后,得到△CA'B'.请先画出变换后的图形,再写出下列结论正确的序号是 . ? ?①△ABC≌△A'B'C; ?②线段AB绕C点旋转180°后,得到线段A'B'; ?③A'B'∥AB; ?④C是线段BB'的中点. ?在第1问的启发下解答下面问题: ?(2)如图②,在△ABC中,∠BAC=120°,D是BC的中点,射线DF交BA于E,交CA的延长线于F,请猜想∠F等于多少度时,BE=CF?(直接写出结果,不需证明) ?(3)如图③,在△ABC中,如果∠BAC≠120°,而(2)中的其他条件不变,若BE=CF的结论仍然成立,那么∠BAC与∠F满足什么数量关系(等式表示)?并加以证明.
参考答案
1. 【答案】A【解析】本题考查中心对称图形的识别,难度较小.在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与原图形重合,这样的图形叫作中心对称图形.根据定义可以判定四个选项中,选项B,C,D都不是中心对称图形,只有A选项是中心对称图形,答案为A.
2. 【答案】C【解析】根据题意可设点P的坐标为(a,-a+3),点Q的坐标为(-a,a-3),?∵Q?是y=3x-5图象上的点,∴-3a-5=a-3,?解得a=-,∴点P的坐标为.故选C.
3. 【答案】D【解析】轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.A是轴对称图形,但不是中心对称图形,故本选项错误;B不是轴对称图形,但是中心对称图形,故本选项错误;C是轴对称图形,但不是中心对称图形,故本选项错误;D是轴对称图形,也是中心对称图形,故本选项正确.故选D.
4. 【答案】C【解析】若(x,y)是关于原点对称,则对称点的坐标为(-x,-y), ?∴(2,-3)关于原点中心对称的点是(-2,3),故选C.
5. 【答案】D【解析】∵△ABC绕点C(0,1)旋转180°得到△A'B'C,?∴点A(a,b)与点A'关于点C(0,1)对称,∴点A'的坐标是(-a,-b+2).?故选D.
6. 【答案】D【解析】∵点P(-20,a)与点Q(b,13)关于原点对称,∴a=-13,b=20,∴a+b=7.故选D.
7. 【答案】B【解析】根据中心对称的定义可知,符合要求的点D有3个,如图所示: ?
8. 【答案】C【解析】由题图知,△ABC与△A'B'C'关于点(-1,0)成中心对称,则点P(a,b)与点P'关于点(-1,0)中心对称,∴P'(-a-2,-b).故选C.
9. 【答案】 ?
10. 【答案】四 ?
11. 【答案】3 ?
(1) 【答案】(-3,-2) ?【解析】如图所示,连接AP并延长至点A',使A'P=AP,则点A'的坐标即为所求; ? ?(2) 【答案】y=2x+4 ?【解析】如图所示,任取直线y=2x上的两点,如O(0,0),B(1,2),则它们关于点P(-1,0)成中心对称的点分别为:A'(-2,0),B'(-3,-2),连接A'B',于是可得所求直线A'B'对应的函数解析式为y=2x+4; ? ?(3) 【答案】y=-x-3 ?【解析】如图所示,任取直线y=2x-3上两点,如A(0,-3),B(1,-1),分别将点A,B绕点P(-1,0)顺时针旋转90°得到A'(-4,-1),B'(-2,-2),连接A'B',于是可得所求直线A'B'对应的函数解析式为y=-x-3. ? ?
12. 【答案】12 ?
13. 【答案】(2,-4) ?
(1) 【答案】如图所示. ? ?(2) 【答案】(0,0). ?(3) 【答案】如图,是中心对称图形. ?
14. 【答案】由对称性得到三角形全等.沿着此思路证明如下: ?∵△ABO与△CDO关于O点成中心对称,∴OB=OD,OA=OC, ?∵AF=CE,∴OF=OE, ?在△DOF和△BOE中,∵OB=OD,∠DOF=∠BOE,OF=OE, ?∴△DOF≌△BOE,∴FD=BE. ?
15. 【答案】(1)如图①.①②③④??(2)60°. ?(3)等量关系:∠BAC=2∠F. ?证明如下:作△DBF'与△FCD关于点D成中心对称,如图②, ?则∠F'=∠F,FC=BF'=BE,∴∠F'=∠F=∠BED=∠FEA,∴∠BAC=2∠F. ? ?
同课章节目录
