湘教版七年级数学上册《第4章图形的认识》单元测试题含答案
文档属性
| 名称 | 湘教版七年级数学上册《第4章图形的认识》单元测试题含答案 | 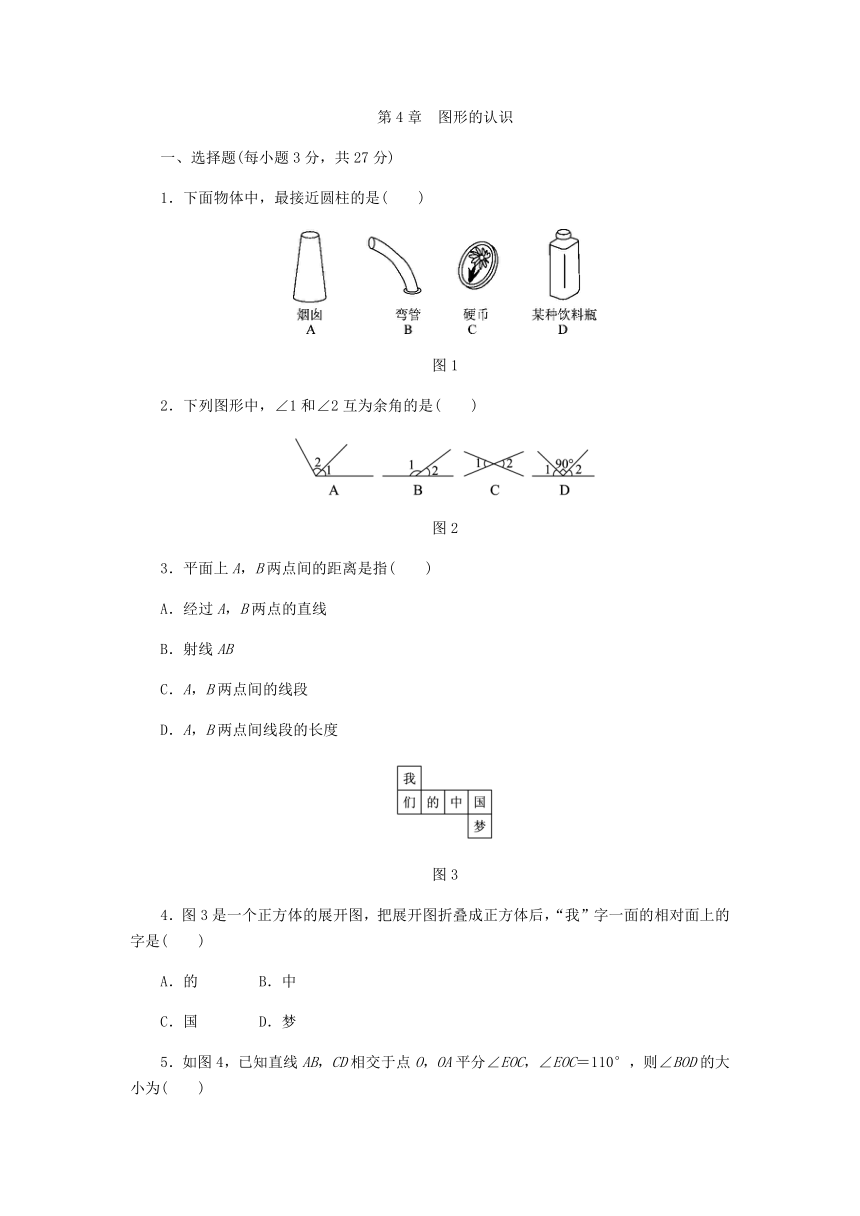 | |
| 格式 | zip | ||
| 文件大小 | 828.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-10 14:36:25 | ||
图片预览




文档简介
第4章 图形的认识
一、选择题(每小题3分,共27分)
1.下面物体中,最接近圆柱的是( )
图1
2.下列图形中,∠1和∠2互为余角的是( )
图2
3.平面上A,B两点间的距离是指( )
A.经过A,B两点的直线
B.射线AB
C.A,B两点间的线段
D.A,B两点间线段的长度
图3
4.图3是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
A.的 B.中
C.国 D.梦
5.如图4,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的大小为( )
A.25° B.35° C.45° D.55°
图4
6.观察图5,下列说法正确的个数是( )
图5
①直线BA和直线AB是同一条直线;②射线AC和射线AD是同一条射线;③AB+BD>AD.
A.0 B.1 C.2 D.3
7.已知∠1=45°24′,∠2=45.3°,∠3=45°18′,则( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.以上都不对
8.不能用一副三角尺拼出的角是( )
A.75° B.100° C.105° D.120°
9.下列生活或生产现象中,可用基本事实“两点之间线段最短”来解释的为( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
D.以上现象都不能用此基本事实解释
二、填空题(每小题4分,共24分)
10.以下图形中,不是锥体的是________.(填序号)
图6
11.乘火车从A站出发,沿途经过2个车站方可到达B站,那么A,B两站之间需要安排________种不同的车票.
12.如图7,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=________°.
图7
13.若∠α的补角是105.5°,则∠α的余角是________.
14.元子权同学每晚19:00都要看央视的《新闻联播》节目,此时钟面上时针与分针的夹角是________度.
15.如图8所示,AB=12,C是AB的中点,D是CB的中点,则AD的长为________.
图8
三、解答题(共49分)
16.(6分)如图9,平面内有四个点A,B,C,D,根据下列语句画图.
(1)画直线AB;
(2)作线段BC;
(3)在直线AB上找一点M,使线段MD与线段MC之和最小.
图9
17.(6分)一个角的补角是它的余角的度数的3倍,求这个角的度数.
18.(8分)在直线a上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
19.(8分)如图10,点A,O,E在同一直线上,∠AOB=40°,∠EOD=25°,OD平分∠COE.
(1)写出图中所有互补的角;
(2)求∠COB的度数.
图10
20.(10分)(1)同一平面内的12条直线两两相交,
最多可以有多少个交点?
(2)是否存在最多交点个数为10的情况?
21.(11分)如图11所示,∠AOB=90°,OE是∠AOC的平分线,OD是∠BOC的平分线,若∠BOC=30°.求:
(1)∠DOE的度数;
(2)若没有给出∠BOC的度数,你能否求出∠DOE的度数?请说明理由;
(3)在(2)的条件下,若∠AOB=α,求∠DOE的度数,你能从中发现什么规律?
图11
答案
1.C
2.D.
3.D.
4.D.
5.D.
6.D.
7.B
8 B.
9.B
10. (3)
11. 12
12. 90
13. 15.5°
14. 150
15. 9
16.解:(1)(2)如图,(3)连接CD,交直线AB于点M,此时线段MD与线段MC之和最小(如图).
17.解:设这个角的度数为x,
则它的补角为180°-x,余角为90°-x.
依题意,得180°-x=3(90°-x),
解得x=45°.
答:这个角的度数为45°.
18.[解析] 题中没有指明点C的具体位置,故应该分两种情况进行分析,从而求得DE的长.
解:(1)如图①,因为AB=16 cm,AC=40 cm,D,E分别是AB,AC的中点,
图①
所以AD=AB=8 cm,
AE=AC=20 cm,
所以DE=AE-AD=20-8=12(cm);
(2)如图②,因为AB=16 cm,AC=40 cm,D,E分别是AB,AC的中点,
图②
所以AD=AB=8 cm,AE=AC=20 cm,
所以DE=AE+AD=20+8=28(cm).
综上所述,点D与点E之间的距离为12 cm或28 cm.
19.解:(1)∠AOB与∠BOE,∠AOC与∠COE,∠AOD与∠DOE,∠COD与∠AOD.
(2)因为∠EOD=25°,OD平分∠COE,
所以∠COE=2∠EOD=50°,
所以∠COB=180°-∠AOB-∠COE=180°-40°-50°=90°.
20.解:(1)12条直线两两相交,最多可以有
n(n-1)=×12×(12-1)=66(个)交点.
(2)存在.同一平面内的5条直线两两相交,最多有10个交点.
21.解:(1)因为OD是∠BOC的平分线,且∠BOC=30°,
所以∠COD=∠BOC=15°.
因为∠AOB=90°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
因为OE是∠AOC的平分线,
所以∠COE=∠AOC=60°.
所以∠DOE=∠COE-∠COD=60°-15°=45°.
(2)能求出∠DOE的度数,∠DOE=45°.理由:
因为∠COE=∠AOC,∠COD=∠BOC,
所以∠DOE=(∠AOC-∠BOC)=∠AOB=45°.
(3)∠DOE=∠COE-∠COD=(∠AOC-∠BOC)=∠AOB=α.
规律:无论∠BOC的大小如何变化,∠DOE始终为∠AOB的度数的一半.
一、选择题(每小题3分,共27分)
1.下面物体中,最接近圆柱的是( )
图1
2.下列图形中,∠1和∠2互为余角的是( )
图2
3.平面上A,B两点间的距离是指( )
A.经过A,B两点的直线
B.射线AB
C.A,B两点间的线段
D.A,B两点间线段的长度
图3
4.图3是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
A.的 B.中
C.国 D.梦
5.如图4,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的大小为( )
A.25° B.35° C.45° D.55°
图4
6.观察图5,下列说法正确的个数是( )
图5
①直线BA和直线AB是同一条直线;②射线AC和射线AD是同一条射线;③AB+BD>AD.
A.0 B.1 C.2 D.3
7.已知∠1=45°24′,∠2=45.3°,∠3=45°18′,则( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.以上都不对
8.不能用一副三角尺拼出的角是( )
A.75° B.100° C.105° D.120°
9.下列生活或生产现象中,可用基本事实“两点之间线段最短”来解释的为( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
D.以上现象都不能用此基本事实解释
二、填空题(每小题4分,共24分)
10.以下图形中,不是锥体的是________.(填序号)
图6
11.乘火车从A站出发,沿途经过2个车站方可到达B站,那么A,B两站之间需要安排________种不同的车票.
12.如图7,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=________°.
图7
13.若∠α的补角是105.5°,则∠α的余角是________.
14.元子权同学每晚19:00都要看央视的《新闻联播》节目,此时钟面上时针与分针的夹角是________度.
15.如图8所示,AB=12,C是AB的中点,D是CB的中点,则AD的长为________.
图8
三、解答题(共49分)
16.(6分)如图9,平面内有四个点A,B,C,D,根据下列语句画图.
(1)画直线AB;
(2)作线段BC;
(3)在直线AB上找一点M,使线段MD与线段MC之和最小.
图9
17.(6分)一个角的补角是它的余角的度数的3倍,求这个角的度数.
18.(8分)在直线a上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E之间的距离.
19.(8分)如图10,点A,O,E在同一直线上,∠AOB=40°,∠EOD=25°,OD平分∠COE.
(1)写出图中所有互补的角;
(2)求∠COB的度数.
图10
20.(10分)(1)同一平面内的12条直线两两相交,
最多可以有多少个交点?
(2)是否存在最多交点个数为10的情况?
21.(11分)如图11所示,∠AOB=90°,OE是∠AOC的平分线,OD是∠BOC的平分线,若∠BOC=30°.求:
(1)∠DOE的度数;
(2)若没有给出∠BOC的度数,你能否求出∠DOE的度数?请说明理由;
(3)在(2)的条件下,若∠AOB=α,求∠DOE的度数,你能从中发现什么规律?
图11
答案
1.C
2.D.
3.D.
4.D.
5.D.
6.D.
7.B
8 B.
9.B
10. (3)
11. 12
12. 90
13. 15.5°
14. 150
15. 9
16.解:(1)(2)如图,(3)连接CD,交直线AB于点M,此时线段MD与线段MC之和最小(如图).
17.解:设这个角的度数为x,
则它的补角为180°-x,余角为90°-x.
依题意,得180°-x=3(90°-x),
解得x=45°.
答:这个角的度数为45°.
18.[解析] 题中没有指明点C的具体位置,故应该分两种情况进行分析,从而求得DE的长.
解:(1)如图①,因为AB=16 cm,AC=40 cm,D,E分别是AB,AC的中点,
图①
所以AD=AB=8 cm,
AE=AC=20 cm,
所以DE=AE-AD=20-8=12(cm);
(2)如图②,因为AB=16 cm,AC=40 cm,D,E分别是AB,AC的中点,
图②
所以AD=AB=8 cm,AE=AC=20 cm,
所以DE=AE+AD=20+8=28(cm).
综上所述,点D与点E之间的距离为12 cm或28 cm.
19.解:(1)∠AOB与∠BOE,∠AOC与∠COE,∠AOD与∠DOE,∠COD与∠AOD.
(2)因为∠EOD=25°,OD平分∠COE,
所以∠COE=2∠EOD=50°,
所以∠COB=180°-∠AOB-∠COE=180°-40°-50°=90°.
20.解:(1)12条直线两两相交,最多可以有
n(n-1)=×12×(12-1)=66(个)交点.
(2)存在.同一平面内的5条直线两两相交,最多有10个交点.
21.解:(1)因为OD是∠BOC的平分线,且∠BOC=30°,
所以∠COD=∠BOC=15°.
因为∠AOB=90°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
因为OE是∠AOC的平分线,
所以∠COE=∠AOC=60°.
所以∠DOE=∠COE-∠COD=60°-15°=45°.
(2)能求出∠DOE的度数,∠DOE=45°.理由:
因为∠COE=∠AOC,∠COD=∠BOC,
所以∠DOE=(∠AOC-∠BOC)=∠AOB=45°.
(3)∠DOE=∠COE-∠COD=(∠AOC-∠BOC)=∠AOB=α.
规律:无论∠BOC的大小如何变化,∠DOE始终为∠AOB的度数的一半.
同课章节目录
