华师大版九年级上《第21章二次根式》综合能力检测试卷含答案
文档属性
| 名称 | 华师大版九年级上《第21章二次根式》综合能力检测试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 666.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-10 00:00:00 | ||
图片预览


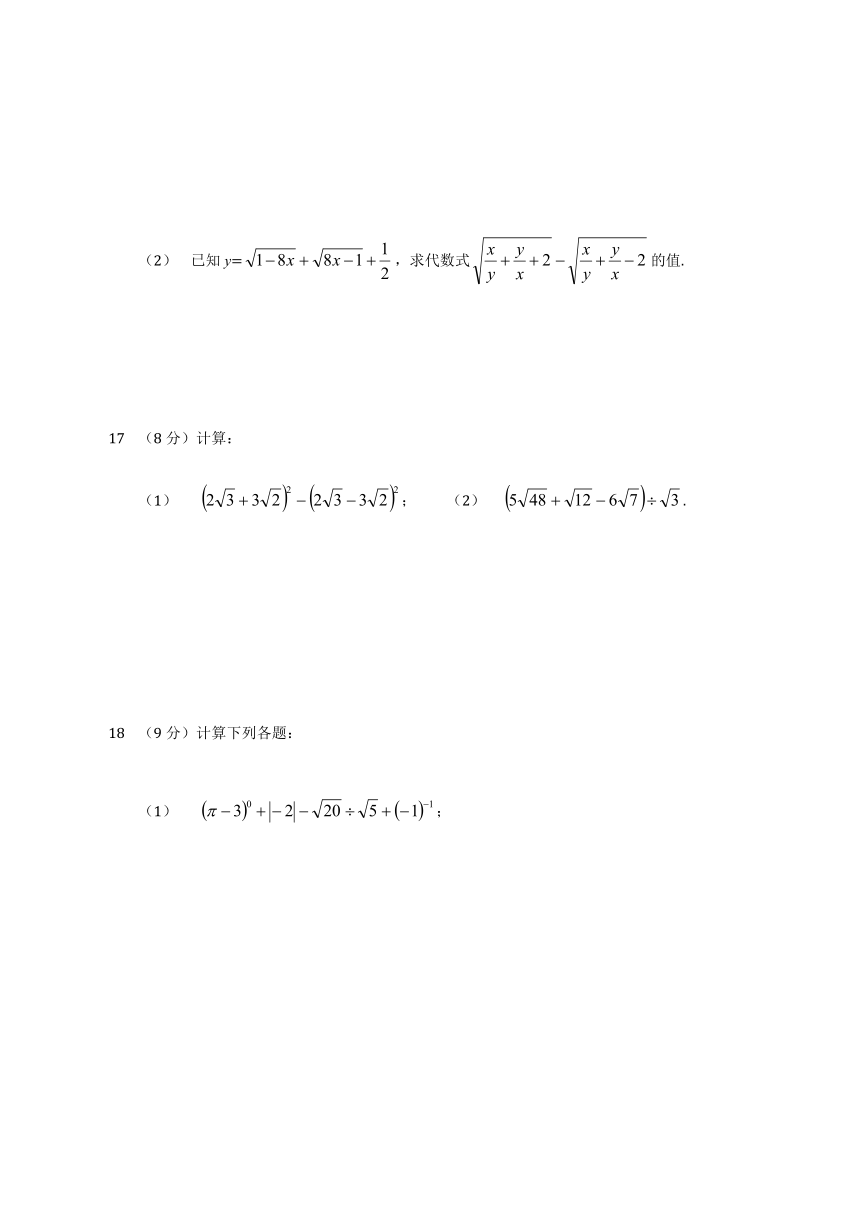
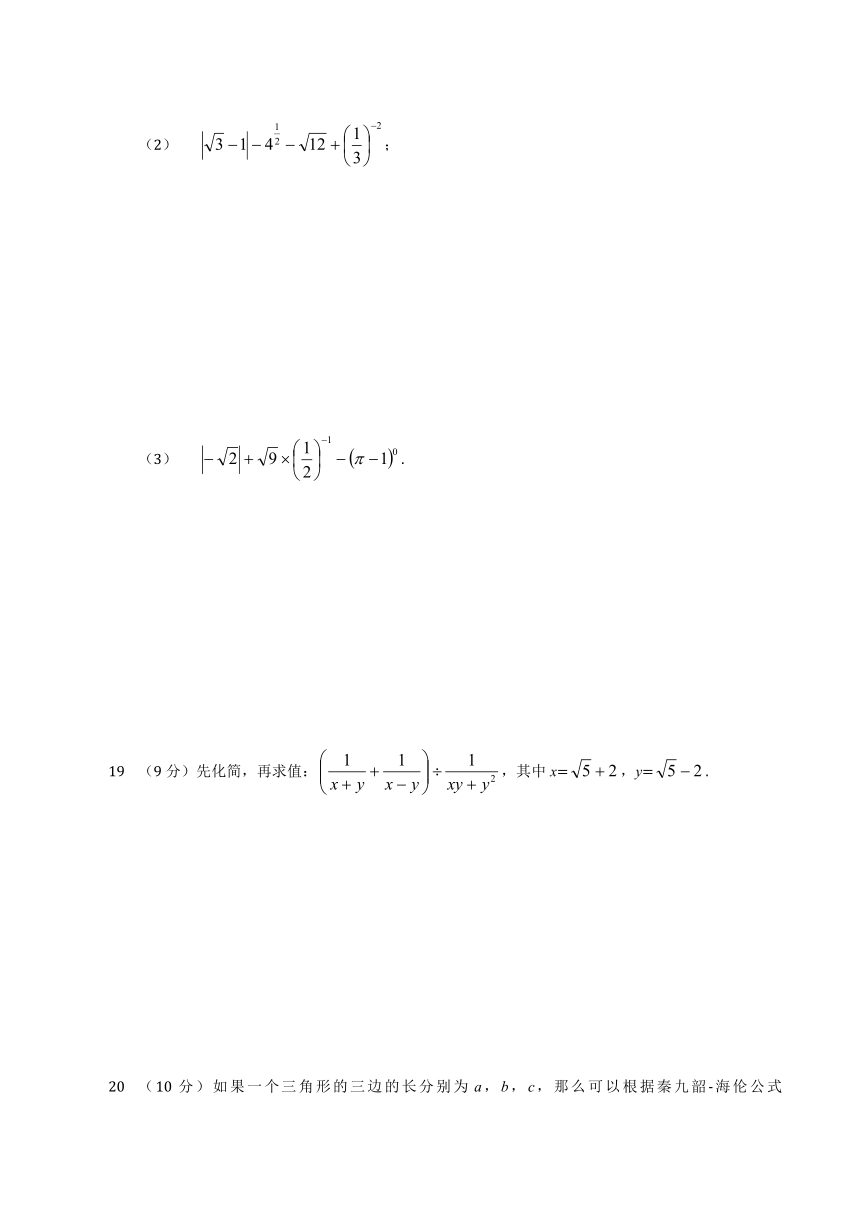

文档简介
第21章 综合能力检测卷
一、 选择题(本大题共10个小题,每题3分,共30分)
1 下列各式:①(x>0);②;③(m>0);④.其中是二次根式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2 函数的自变量x的取值范围是( )
A. x≥1 B. x≥1且x≠3 C. x≠3 D. 1≤x≤3
3 下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4 若实数x,y满足,则x+y的值是( )
A. 1 B. C. 2 D.
5 下列根式中能与合并的是( ) A. B. C. D. 8
6 下列各式计算正确的是( ) A. B. C. D.
7 若a,b是有理数且,则a+b等于( ) A. 5 B. C. 6 D. 7
8 已知实数a,b在数轴上对应的位置如图所示,则( )
A. b-a B. 2-a-b C. a-b D. 2+a-b
9 对于任意的正数m,n,定义运算:,计算(3※2)×(8※12)的结果为( ) A. B. 2 C. D. 20
10 按如图所示的程序计算,若开始图稿的n值为,则最后输出的t值为( )
A. 14 B. 16 C. D.
二、填空题(本大题共5个小题,每题3分,共15分)
11 若最简二次根式与是同类二次根式,则a=_______________.
12 计算:________________.
13 计算:____________________.
14 规定两种新运算:a⊕b=ab,c*d=,如3⊕2=32=9,2*3=,那么12*(⊕3)=_______________.
15 若x,y分别为的整数部分和小数部分,则2xy-y2=_________________.
三、解答题(本大题共8个小题,共75分)
16 (8分)解答下列各题:
(1) 已知已知x=1,y=1+,求的值;
(2) 已知y=,求代数式的值.
17 (8分)计算:
(1) ; (2) .
18 (9分)计算下列各题:
(1) ;
(2) ;
(3) .
19 (9分)先化简,再求值:,其中x=,y=.
20 (10分)如果一个三角形的三边的长分别为a,b,c,那么可以根据秦九韶-海伦公式[其中]求出这个三角形的面积,试求出三边长a,b,c分别为,3,的三角形的面积。
21 (10分)观察下列各式及证明过程:
① ;②;③.
验证:;
;
.
(1) 按照上述等式及验证过程的基本思想,猜想的变形结果并进行验证;
(2) 针对上述各式反映的规律,写出用n(n为大于等于1的自然数)表示的等式,并验证.
22 (10分)【知识链接】
(i) 有理化因式:如果两个含有二次根式的非零代数式相乘,它们的各不含有二次根式,就说这两个非零代数式互为有理化因式。 例如:与互为有理化因式;与互为有理化因式.
(ii) 分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如: ,.
【知识理解】
(1) 填空:的一个有理化因式是_____________________.
(2) 仿照(ⅱ)直接写出下列各式分母有理化后结果: ①__________________.②__________________.
【启发运用】
(3) 计算:
23 (11分)读取表格中的信息,解决问题
(1) 计算,,,并猜想的值;
(2) 求满足的n可以取得的最小正整数值.
答案:
1 B 2 B 3 B 4 B 5 A
6 C 7 B 8 C 9 B 10 C
11 7
12
13
14
15 5
16 (1)x2+y2-xy-2x=(x-y)2+xy-2(x-y).
∵,,∴,xy=-1,
∴原式==
(2)根据题意,得,解得,则,
则1.
17 (1) 24 (2)
18 (1) 0; (2) (3) 5
19 化简为:原式=,当时,原式=
20 3
21 (1). 验证:.
(2) 或, 验证:22. (1)(答案不唯一) (2)① ②
(3)
23. ,
,
……
.
(2)n可以取得的最小正整数值是7.
一、 选择题(本大题共10个小题,每题3分,共30分)
1 下列各式:①(x>0);②;③(m>0);④.其中是二次根式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2 函数的自变量x的取值范围是( )
A. x≥1 B. x≥1且x≠3 C. x≠3 D. 1≤x≤3
3 下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4 若实数x,y满足,则x+y的值是( )
A. 1 B. C. 2 D.
5 下列根式中能与合并的是( ) A. B. C. D. 8
6 下列各式计算正确的是( ) A. B. C. D.
7 若a,b是有理数且,则a+b等于( ) A. 5 B. C. 6 D. 7
8 已知实数a,b在数轴上对应的位置如图所示,则( )
A. b-a B. 2-a-b C. a-b D. 2+a-b
9 对于任意的正数m,n,定义运算:,计算(3※2)×(8※12)的结果为( ) A. B. 2 C. D. 20
10 按如图所示的程序计算,若开始图稿的n值为,则最后输出的t值为( )
A. 14 B. 16 C. D.
二、填空题(本大题共5个小题,每题3分,共15分)
11 若最简二次根式与是同类二次根式,则a=_______________.
12 计算:________________.
13 计算:____________________.
14 规定两种新运算:a⊕b=ab,c*d=,如3⊕2=32=9,2*3=,那么12*(⊕3)=_______________.
15 若x,y分别为的整数部分和小数部分,则2xy-y2=_________________.
三、解答题(本大题共8个小题,共75分)
16 (8分)解答下列各题:
(1) 已知已知x=1,y=1+,求的值;
(2) 已知y=,求代数式的值.
17 (8分)计算:
(1) ; (2) .
18 (9分)计算下列各题:
(1) ;
(2) ;
(3) .
19 (9分)先化简,再求值:,其中x=,y=.
20 (10分)如果一个三角形的三边的长分别为a,b,c,那么可以根据秦九韶-海伦公式[其中]求出这个三角形的面积,试求出三边长a,b,c分别为,3,的三角形的面积。
21 (10分)观察下列各式及证明过程:
① ;②;③.
验证:;
;
.
(1) 按照上述等式及验证过程的基本思想,猜想的变形结果并进行验证;
(2) 针对上述各式反映的规律,写出用n(n为大于等于1的自然数)表示的等式,并验证.
22 (10分)【知识链接】
(i) 有理化因式:如果两个含有二次根式的非零代数式相乘,它们的各不含有二次根式,就说这两个非零代数式互为有理化因式。 例如:与互为有理化因式;与互为有理化因式.
(ii) 分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如: ,.
【知识理解】
(1) 填空:的一个有理化因式是_____________________.
(2) 仿照(ⅱ)直接写出下列各式分母有理化后结果: ①__________________.②__________________.
【启发运用】
(3) 计算:
23 (11分)读取表格中的信息,解决问题
(1) 计算,,,并猜想的值;
(2) 求满足的n可以取得的最小正整数值.
答案:
1 B 2 B 3 B 4 B 5 A
6 C 7 B 8 C 9 B 10 C
11 7
12
13
14
15 5
16 (1)x2+y2-xy-2x=(x-y)2+xy-2(x-y).
∵,,∴,xy=-1,
∴原式==
(2)根据题意,得,解得,则,
则1.
17 (1) 24 (2)
18 (1) 0; (2) (3) 5
19 化简为:原式=,当时,原式=
20 3
21 (1). 验证:.
(2) 或, 验证:22. (1)(答案不唯一) (2)① ②
(3)
23. ,
,
……
.
(2)n可以取得的最小正整数值是7.
