华东师大九年级上《第24章解直角三角形》综合能力检测卷含简略答案
文档属性
| 名称 | 华东师大九年级上《第24章解直角三角形》综合能力检测卷含简略答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-10 00:00:00 | ||
图片预览



文档简介
第24章 综合能力检测卷
一、 选择题(本大题共10个小题,每题3分,共30分)
1. cos 60°的值等于( ) A. B. C. D.
2. 已知点A(t,3)在第一象限,OA与x轴所夹锐角为α,tan α=,则t的值是( ) A. 1 B. 1.5 C. 2 D. 3
3. 如图,在四边形ABCD中,AD∥CD,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB=( )
A. 3 B. 6 C. 8 D. 9
4. 在Rt△ABC中,∠C=90°,sin A=,则sin B的值为( ) A. B. C. D.
5. △ABC在网格中的位置如图所示(每个小正方形的国边长均为1),AD⊥BC于D,下列四个选项中,错误的是( )
A. sinα=cosα B. tan∠ACB=2 C. sinβ=cosβ D.tanα=1
6. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度,如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB’的位置,测得∠PB’C=α(B’C为水平线),测角仪B’D的高度为1米,则旗杆PA的高度为( )
A. 米 B. 米 C. 米 D. 米
7. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离场面的高度为( )
A. 5 m B. m C. 10 m D. m
8. 如图,在△ABC中,AD⊥BC垂足为点D,若AC=,∠C=45°,tan∠ABC=3,则BD等于( )
A. 2 B. 3 C. D.
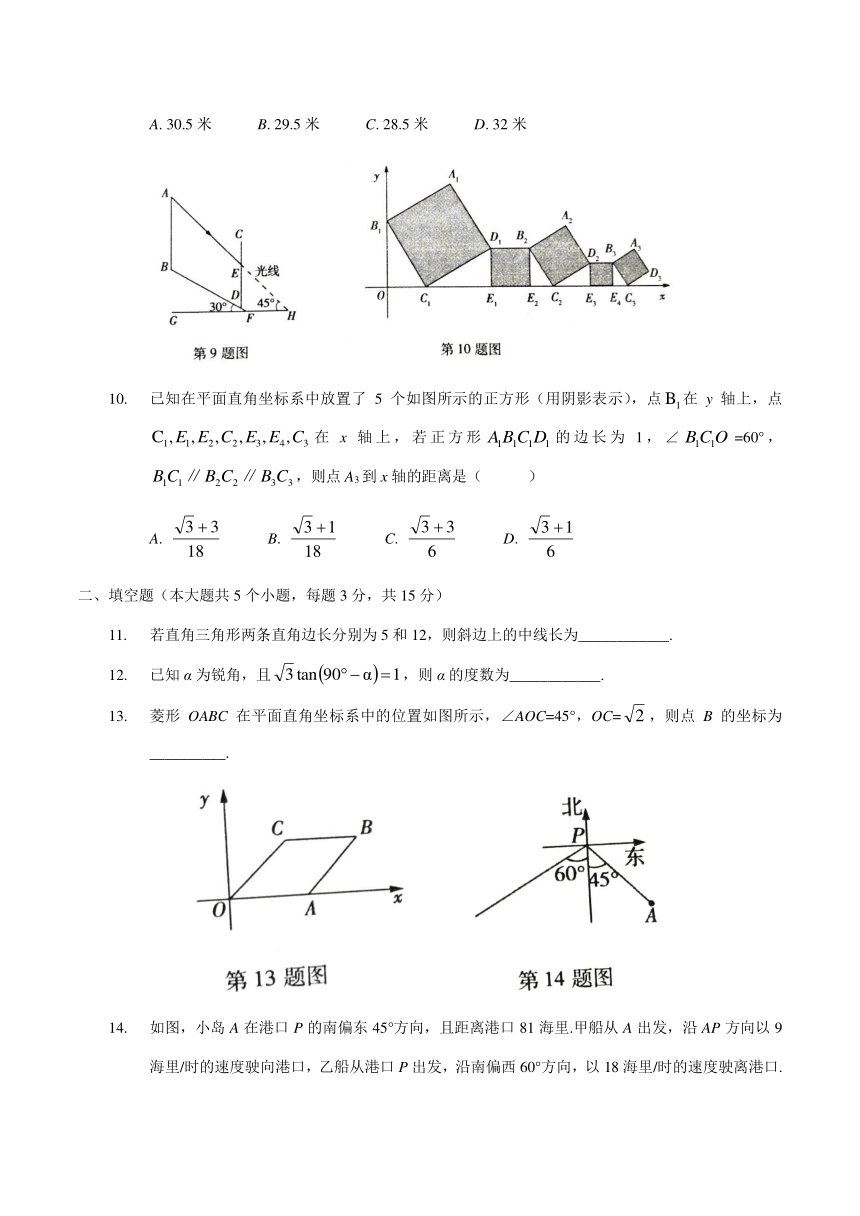
9. 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线与水平地面夹角为45°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为(参考数据:,)( )
A. 30.5米 B. 29.5米 C. 28.5米 D. 32米
10. 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点在y轴上,点在x轴上,若正方形的边长为1,∠=60°,,则点A3到x轴的距离是( ) A. B. C. D.
二、填空题(本大题共5个小题,每题3分,共15分)
11. 若直角三角形两条直角边长分别为5和12,则斜边上的中线长为____________.
12. 已知α为锐角,且,则α的度数为____________.
13. 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为__________.
14. 如图,小岛A在港口P的南偏东45°方向,且距离港口81海里.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏西60°方向,以18海里/时的速度驶离港口.两船同时出发,当甲船在乙船的正东方向时,行驶的时间为__________小时.(结果保留根号)
15. 查阅资料发现:sin(-60°)=,,.据此判断下列等式:①;②;③;④.其中成立的是_____________.(填序号)
三、解答题(本大题共8个小时,共75分)
16. (8分)计算:
(1) ; (2) .
17. (8分)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若c=10,tan A=,求a,b及cos B的值.
18. (8分)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD,CB相交于点H,E,AH=2CH.
(1) 求的值;
(2) 如果CD=,求BE的值.
19. (8分)数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题
测量教学楼高度
方案
一
二
图示
测得数据
CD=6.9米,∠ACG=22°,
∠BCG=13°.
EF=10米,∠AEB=32°,
∠AFB=43°
参考数据
Sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin13°≈0.22,cos13°≈0.97,tan13°≈0.23.
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.
请你选择其中的一种方案,求教学楼的高度.(结果保留整数)
20. (10分)某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在D点测得旗杆顶端E点的仰角为30°,已知小明和小军相距6米,小明的身高(AB)为1.5米,小军的身高(CD)为1.75米,求旗杆EF的高.(结果精确到0.1,参考数据:)
21. (10分 )如图所示,接上级气象部门通知:有一台风将在南海附近登陆,台风登陆中心为C地,已知港口A位于城市C的北偏东15°方向上,且两地相距240 km.该台风中心以20 km/h的速度沿北偏乐45°的CF方向移动,在距离台风中心130 km内的地方都要受到影响.台风中心在移动过程中,港口A是否会受影响?若受影响,求台风影响港口的时间;若不受影响,说明理由.
22. (11分)某海域有A,B两个港口,B港口在A港口的北偏西30°的方向上,距A港口60海里.有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处.求该船与B港口之间的距离即CB的长.(结果保留根号)
23. (12分)图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15 cm,,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)广园较平衡.
(1) 求平衡放置时灯座DC与灯杆DE的夹角的大小;
(2) 为保护视力,写字时眼睛离桌面的距离应保持在30 cm,为防止台灯刺眼,点A离桌面的距离应不超过30 cm,求台灯平衡放置时∠ABE的最大值.(结果精确到0.01°,参考数据:,sin7.70°≈0.134,cos82.30°≈0.134)
参考答案
一、 选择题
1. A 2. C 3. B 4. D 5. C
6. A 7. B 8. A 9. B 10. D
二、填空题
11. 6.5 12. 60° 13. (,1) 14. 15. ②③④
三、解答题
16. (1) (2)
17. ,,
18. (1) (2)BE=3
19. 答:教学楼的高为19米.
20. 答:旗杆EF的约为10.3米.
21. 答:台风中心在移动过程中,港口A受影响,台风影响A的时间为5小时.
22. 答:该船与B港口之间的距离即CB的长为海里.
23. (1)平衡放置时灯座CD与灯杆DE的夹角为60°.
(2)∠ABE的最大值为97.7°.
一、 选择题(本大题共10个小题,每题3分,共30分)
1. cos 60°的值等于( ) A. B. C. D.
2. 已知点A(t,3)在第一象限,OA与x轴所夹锐角为α,tan α=,则t的值是( ) A. 1 B. 1.5 C. 2 D. 3
3. 如图,在四边形ABCD中,AD∥CD,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB=( )
A. 3 B. 6 C. 8 D. 9
4. 在Rt△ABC中,∠C=90°,sin A=,则sin B的值为( ) A. B. C. D.
5. △ABC在网格中的位置如图所示(每个小正方形的国边长均为1),AD⊥BC于D,下列四个选项中,错误的是( )
A. sinα=cosα B. tan∠ACB=2 C. sinβ=cosβ D.tanα=1
6. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度,如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB’的位置,测得∠PB’C=α(B’C为水平线),测角仪B’D的高度为1米,则旗杆PA的高度为( )
A. 米 B. 米 C. 米 D. 米
7. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离场面的高度为( )
A. 5 m B. m C. 10 m D. m
8. 如图,在△ABC中,AD⊥BC垂足为点D,若AC=,∠C=45°,tan∠ABC=3,则BD等于( )
A. 2 B. 3 C. D.
9. 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线与水平地面夹角为45°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为(参考数据:,)( )
A. 30.5米 B. 29.5米 C. 28.5米 D. 32米
10. 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点在y轴上,点在x轴上,若正方形的边长为1,∠=60°,,则点A3到x轴的距离是( ) A. B. C. D.
二、填空题(本大题共5个小题,每题3分,共15分)
11. 若直角三角形两条直角边长分别为5和12,则斜边上的中线长为____________.
12. 已知α为锐角,且,则α的度数为____________.
13. 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为__________.
14. 如图,小岛A在港口P的南偏东45°方向,且距离港口81海里.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏西60°方向,以18海里/时的速度驶离港口.两船同时出发,当甲船在乙船的正东方向时,行驶的时间为__________小时.(结果保留根号)
15. 查阅资料发现:sin(-60°)=,,.据此判断下列等式:①;②;③;④.其中成立的是_____________.(填序号)
三、解答题(本大题共8个小时,共75分)
16. (8分)计算:
(1) ; (2) .
17. (8分)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若c=10,tan A=,求a,b及cos B的值.
18. (8分)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD,CB相交于点H,E,AH=2CH.
(1) 求的值;
(2) 如果CD=,求BE的值.
19. (8分)数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题
测量教学楼高度
方案
一
二
图示
测得数据
CD=6.9米,∠ACG=22°,
∠BCG=13°.
EF=10米,∠AEB=32°,
∠AFB=43°
参考数据
Sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin13°≈0.22,cos13°≈0.97,tan13°≈0.23.
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.
请你选择其中的一种方案,求教学楼的高度.(结果保留整数)
20. (10分)某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在D点测得旗杆顶端E点的仰角为30°,已知小明和小军相距6米,小明的身高(AB)为1.5米,小军的身高(CD)为1.75米,求旗杆EF的高.(结果精确到0.1,参考数据:)
21. (10分 )如图所示,接上级气象部门通知:有一台风将在南海附近登陆,台风登陆中心为C地,已知港口A位于城市C的北偏东15°方向上,且两地相距240 km.该台风中心以20 km/h的速度沿北偏乐45°的CF方向移动,在距离台风中心130 km内的地方都要受到影响.台风中心在移动过程中,港口A是否会受影响?若受影响,求台风影响港口的时间;若不受影响,说明理由.
22. (11分)某海域有A,B两个港口,B港口在A港口的北偏西30°的方向上,距A港口60海里.有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处.求该船与B港口之间的距离即CB的长.(结果保留根号)
23. (12分)图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15 cm,,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)广园较平衡.
(1) 求平衡放置时灯座DC与灯杆DE的夹角的大小;
(2) 为保护视力,写字时眼睛离桌面的距离应保持在30 cm,为防止台灯刺眼,点A离桌面的距离应不超过30 cm,求台灯平衡放置时∠ABE的最大值.(结果精确到0.01°,参考数据:,sin7.70°≈0.134,cos82.30°≈0.134)
参考答案
一、 选择题
1. A 2. C 3. B 4. D 5. C
6. A 7. B 8. A 9. B 10. D
二、填空题
11. 6.5 12. 60° 13. (,1) 14. 15. ②③④
三、解答题
16. (1) (2)
17. ,,
18. (1) (2)BE=3
19. 答:教学楼的高为19米.
20. 答:旗杆EF的约为10.3米.
21. 答:台风中心在移动过程中,港口A受影响,台风影响A的时间为5小时.
22. 答:该船与B港口之间的距离即CB的长为海里.
23. (1)平衡放置时灯座CD与灯杆DE的夹角为60°.
(2)∠ABE的最大值为97.7°.
