华东师大八年级上《第13章全等三角形》综合能力检测试卷含答案
文档属性
| 名称 | 华东师大八年级上《第13章全等三角形》综合能力检测试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-11 11:36:45 | ||
图片预览



文档简介
第13章 综合能力检测卷
一、 选择题(本大题共10个小题,每题3分,共3分)
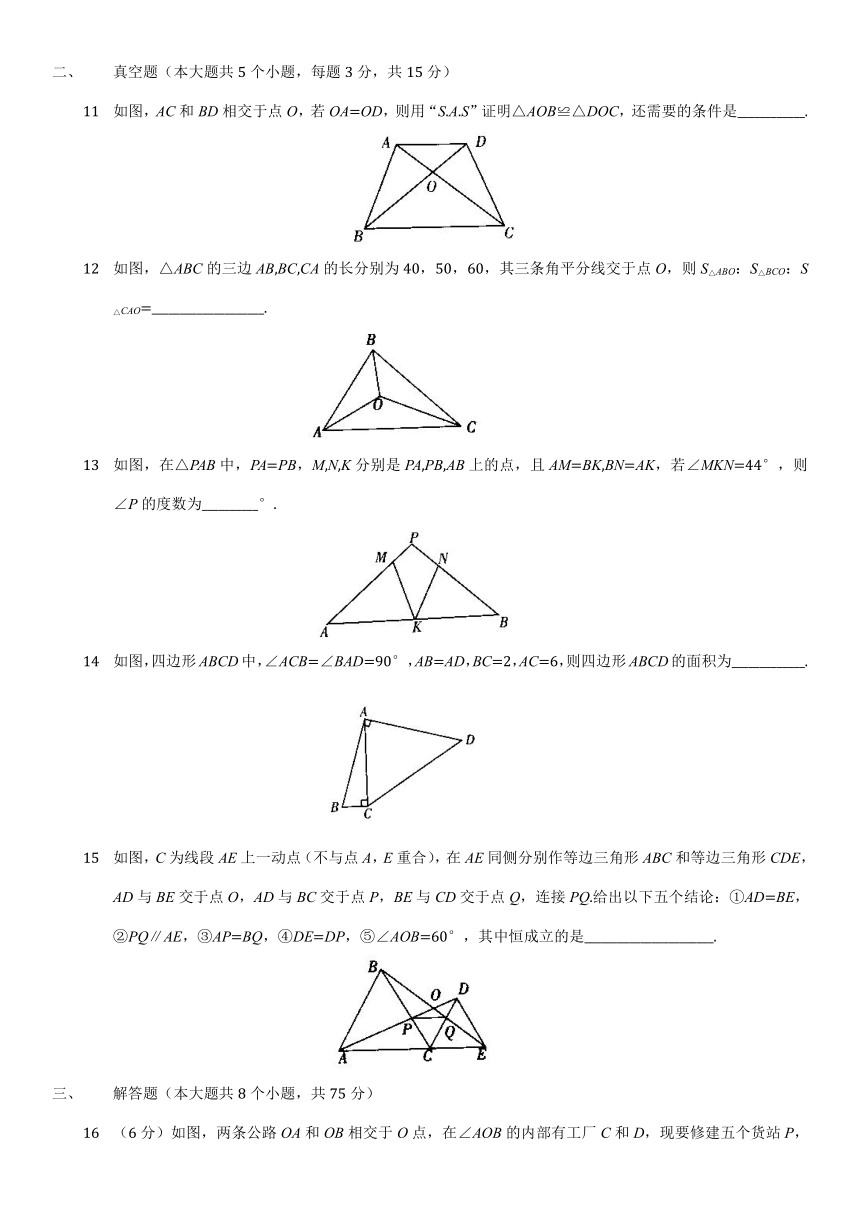
1 下列命题中,是真命题的是() A. 若a·b>0,则a>0,b>0 B. 若a·b<0,则a<0,b<0 C. 若a·b=0,则a=0且b=0 D. 若a·b=0,则a=0或b=0
2 如图,∠MAN=63°,进行如下操作:以射线AM上一点B为圆心,以线段BA的长为半径作弧,交射线AN于点C,连接BC,则∠BCN的度数是() A. 54° B. 63° C. 117° D. 126°
3 如图,已知MB=ND,∠MNA=∠NDC,下列条件中不能判定△ABM≌△CDN的是() A. ∠M=∠N B. AM∥CN C. AB=CD D. AM=CN
4 在△ABC中,AB=AC,AD⊥BC,垂足为D,若△ABC的周长为36 cm,△ADC的周长为30 cm,则AD的长为() A. 6 cm B. 8 cm C. 12 cm D. 20 cm
5 如图,四边形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连接DE,则四边形ABED的周长等于() A. 17 B. 18 C. 19 D. 20
6 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AD=BD,AB=ED,BC=BE,则∠ACB等于() A. ∠EDB B. ∠BED C. ∠AFB D. 2∠ABF
7 如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D,E,F分别是CD,AD上的点,且CE=AF.如果∠AED=62°,那么∠DBF= () A. 62° B. 38° C. 28° D. 26°
8 如图,在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,交CD于点F,下列结论一定成立的是() A. AB=BF B. AE=ED C. AD=DC D. ∠ABE=∠DFE
9 如图,在∠MON的两边上截取OA=OB,CO=DO,连接AD,BC,AD与BC交于点P,则下列结论:①△AOD≌△BOC;②△APC≌△BPD;③P在∠AOB的平分线上.其中正确的是() A. 只有① B. 只有② C. 只有①② D. 只有①②③
10 已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则最多可画这样的直线() A. 3条 B. 4条 C. 5条 D. 6条
二、 真空题(本大题共5个小题,每题3分,共15分)
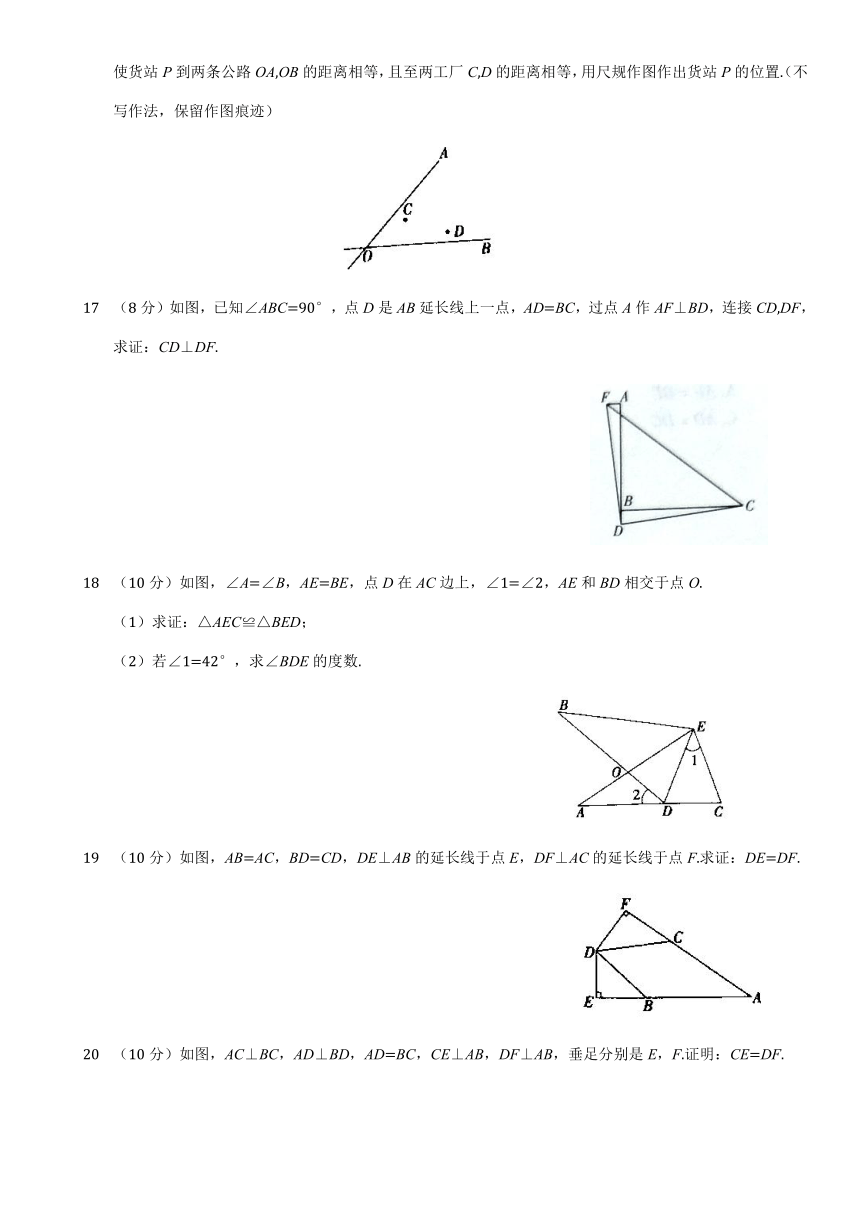
11 如图,AC和BD相交于点O,若OA=OD,则用“S.A.S”证明△AOB≌△DOC,还需要的条件是____________.
12 如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=____________________.
13 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为__________°.
14 如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,则四边形ABCD的面积为_____________.
15 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.给出以下五个结论:①AD=BE,②PQ∥AE,③AP=BQ,④DE=DP,⑤∠AOB=60°,其中恒成立的是_______________________.
三、 解答题(本大题共8个小题,共75分)
16 (6分)如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建五个货站P,使货站P到两条公路OA,OB的距离相等,且至两工厂C,D的距离相等,用尺规作图作出货站P的位置.(不写作法,保留作图痕迹)
17 (8分)如图,已知∠ABC=90°,点D是AB延长线上一点,AD=BC,过点A作AF⊥BD,连接CD,DF,求证:CD⊥DF.
18 (10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O. (1)求证:△AEC≌△BED; (2)若∠1=42°,求∠BDE的度数.
19 (10分)如图,AB=AC,BD=CD,DE⊥AB的延长线于点E,DF⊥AC的延长线于点F.求证:DE=DF.
20 (10分)如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F.证明:CE=DF.
21 (10分)如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.. (1)求证:OB=OC; (2)若∠ABC=50°,天津市∠BOC的度数。
22 (10分)如图,在△ABC中,∠CAB的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF⊥AC,交AC的延长线于点F,作DM⊥AB于点M. (1)猜想CF和BM之间有何数量关系,并说明理由; (2)求证:AB-AC=2CF.
23 (11分)【问题提出】 如图1,已知△ABC是等边三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF. 试证明:AB=DB+AF. 【类比探究】 (1)如图2,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由. (2)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由。
答案:
1 D 2 C 3 D 4 C 5 A
6 C 7 C 8 A 9 D 10 B
11 OB=OC
12 4:5:6
13 92
14 24
15 ①②③⑤
16 如图所示,连接CD,作CD的垂直平分线与∠AOB的平分线,两直线的交点P即所示作的货站P的位置。
17 ∵AF⊥AD,∠ABC=90°, ∴∠FAD=∠DBC=90°, 在△AFD和△BDC中, ∴△AFD≌△BDC(S.A.S), ∴∠ADF=∠BCD, ∵∠BDC+∠BCD=90°, ∴∠BDC+∠ADF=90°即∠CDF=90°, ∴CD⊥DF.
18 (1)∵AE和BD相交于点O, ∴∠AOD=∠BOE, 又∵∠A=∠B, ∴∠BEO=∠2, ∴∠1=∠BEO, ∴∠AEC=∠BED 在△AEC和△BED中, ∴△AEC≌△BED. (2)由(1)知△AEC≌△BED, ∴EC=ED,∠C=∠BDE. 又∵∠1=42°, ∴∠C=∠EDC=69°, ∴∠BDE=∠C=69°.
19 连接AD. 在△ABD和△ACD中, ∴△ABD≌△ACD(S.S.S), ∴∠ACD=∠ABD, ∴∠DCF=∠DBE. 又∵∠DFC=∠DEB=90°,DC=DB. ∴△DFC≌△DEB(A.A.S),∴DE=DF.
20 ∵AC⊥BC,AD⊥BD, ∴△ABC和△ABD均是直角三角形. 在Rt△ABC和Rt△BAD中, ∴Rt△ABC≌Rt△BAD(H.L.), ∴AC=BD,∠CAB=∠DBA. ∴△ACE≌△BDF(A.A.S.), ∴DE=DF.
21 (1)∵AB=AC, ∴∠ABC=∠ACB, ∵BD,CE是△ABC的两条高, ∴∠BEC=∠CDB=90°, 又∵BC=CB, ∴△BEC≌△CDB(A.A.S.), ∴∠DBC=∠ECB, ∴OB=OC. (2)∵∠ABC=50°,AB=AC, ∴∠A=180°-2×50°=80°, ∵∠DOE+∠A=180°, ∴∠DOE=180°-∠A=180°-80°=100°, ∴∠BOC=∠DOE=100°.
22 (1)CF=BN.理由如下: 如图,连接CD,DB, ∵AD平分∠CAB,DF⊥AC,DM⊥AB, ∴DF=DM. ∵DE垂直平分BC, ∴CD=BD. 又∵∠CFD=∠DMB=90°, ∴Rt△CDF≌Rt△BDM, ∴CF=BM. (2)∵AD=AD,DF=DM,∠AFD=∠AMD=90°, ∴Rt△AFD≌Rt△AMD, ∴AF=AM. ∵AB=AM+BM,AF=AC+CF,AF=AM,BM=CF, ∴AB=AC+2CF, ∴AB-AC=2CF.
23 【问题提出】 由旋转的性质知BE=AF,∠ABC=∠FAC,EC=FC,∠ECF=60°, ∴△ECF是等边三角形,∴∠FEC=60°, ∴∠AEF+∠BEC=120°. ∵△ABC是等边三角形,∴∠BAC=∠ABC=60°, ∴∠BEC+∠BCE=120°, ∴∠AEF=∠BCE. ∵ED=EC,∴∠D=∠ECD, ∴∠AEF=∠D. ∵∠FAC=60°,∠BAC=60°,∴∠EAF=120°. ∵∠ABC=60°,∴∠DBE=120°,∴∠EAF=∠DBE. 在△AEF和△BDE中, ∵∠AEF=∠BDE,∠EAF=∠DBE,AF=BE, ∴△AEF≌△BDE(A.A.S.),∴AB=DB+AF. 【类比探究】 (1)AB=DB-AF.理由如下: 由旋转的性质知BE=AF,∠EBC=∠FAC,EC=FC,∠ECF=60°,∴△ECF是等边三角形。 ∴∠FEC=60°,∴∠FEA+∠BEC=60°, ∵△ABC是等边三角形,∴∠BAC=∠ABC=60°, ∴∠BEC+∠BCE=60°,∴∠FEA=∠BCE. ∵DE=CE,∴∠D=∠BCE,∴∠FEA=∠D. ∵∠ABC=60°,∴∠DBE=60°,∠EBC=120°, ∴∠FAC=∠EBC=120° 在△AEF和△BDE中, ∵∠FEA=∠EDB,∠FAE=∠EBD,AF=BE, ∴△AEF≌△BDE(A.A.S.),∴AE=BD. ∵AB=AE-BE,AF=BE,AE=BD,∴AB=DB-AF. (2)AB=AF-DB. 只画出图1、图2中的一个图即可。
一、 选择题(本大题共10个小题,每题3分,共3分)
1 下列命题中,是真命题的是() A. 若a·b>0,则a>0,b>0 B. 若a·b<0,则a<0,b<0 C. 若a·b=0,则a=0且b=0 D. 若a·b=0,则a=0或b=0
2 如图,∠MAN=63°,进行如下操作:以射线AM上一点B为圆心,以线段BA的长为半径作弧,交射线AN于点C,连接BC,则∠BCN的度数是() A. 54° B. 63° C. 117° D. 126°
3 如图,已知MB=ND,∠MNA=∠NDC,下列条件中不能判定△ABM≌△CDN的是() A. ∠M=∠N B. AM∥CN C. AB=CD D. AM=CN
4 在△ABC中,AB=AC,AD⊥BC,垂足为D,若△ABC的周长为36 cm,△ADC的周长为30 cm,则AD的长为() A. 6 cm B. 8 cm C. 12 cm D. 20 cm
5 如图,四边形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连接DE,则四边形ABED的周长等于() A. 17 B. 18 C. 19 D. 20
6 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AD=BD,AB=ED,BC=BE,则∠ACB等于() A. ∠EDB B. ∠BED C. ∠AFB D. 2∠ABF
7 如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D,E,F分别是CD,AD上的点,且CE=AF.如果∠AED=62°,那么∠DBF= () A. 62° B. 38° C. 28° D. 26°
8 如图,在Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,交CD于点F,下列结论一定成立的是() A. AB=BF B. AE=ED C. AD=DC D. ∠ABE=∠DFE
9 如图,在∠MON的两边上截取OA=OB,CO=DO,连接AD,BC,AD与BC交于点P,则下列结论:①△AOD≌△BOC;②△APC≌△BPD;③P在∠AOB的平分线上.其中正确的是() A. 只有① B. 只有② C. 只有①② D. 只有①②③
10 已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则最多可画这样的直线() A. 3条 B. 4条 C. 5条 D. 6条
二、 真空题(本大题共5个小题,每题3分,共15分)
11 如图,AC和BD相交于点O,若OA=OD,则用“S.A.S”证明△AOB≌△DOC,还需要的条件是____________.
12 如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=____________________.
13 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为__________°.
14 如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,则四边形ABCD的面积为_____________.
15 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.给出以下五个结论:①AD=BE,②PQ∥AE,③AP=BQ,④DE=DP,⑤∠AOB=60°,其中恒成立的是_______________________.
三、 解答题(本大题共8个小题,共75分)
16 (6分)如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建五个货站P,使货站P到两条公路OA,OB的距离相等,且至两工厂C,D的距离相等,用尺规作图作出货站P的位置.(不写作法,保留作图痕迹)
17 (8分)如图,已知∠ABC=90°,点D是AB延长线上一点,AD=BC,过点A作AF⊥BD,连接CD,DF,求证:CD⊥DF.
18 (10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O. (1)求证:△AEC≌△BED; (2)若∠1=42°,求∠BDE的度数.
19 (10分)如图,AB=AC,BD=CD,DE⊥AB的延长线于点E,DF⊥AC的延长线于点F.求证:DE=DF.
20 (10分)如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F.证明:CE=DF.
21 (10分)如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.. (1)求证:OB=OC; (2)若∠ABC=50°,天津市∠BOC的度数。
22 (10分)如图,在△ABC中,∠CAB的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF⊥AC,交AC的延长线于点F,作DM⊥AB于点M. (1)猜想CF和BM之间有何数量关系,并说明理由; (2)求证:AB-AC=2CF.
23 (11分)【问题提出】 如图1,已知△ABC是等边三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF. 试证明:AB=DB+AF. 【类比探究】 (1)如图2,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由. (2)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由。
答案:
1 D 2 C 3 D 4 C 5 A
6 C 7 C 8 A 9 D 10 B
11 OB=OC
12 4:5:6
13 92
14 24
15 ①②③⑤
16 如图所示,连接CD,作CD的垂直平分线与∠AOB的平分线,两直线的交点P即所示作的货站P的位置。
17 ∵AF⊥AD,∠ABC=90°, ∴∠FAD=∠DBC=90°, 在△AFD和△BDC中, ∴△AFD≌△BDC(S.A.S), ∴∠ADF=∠BCD, ∵∠BDC+∠BCD=90°, ∴∠BDC+∠ADF=90°即∠CDF=90°, ∴CD⊥DF.
18 (1)∵AE和BD相交于点O, ∴∠AOD=∠BOE, 又∵∠A=∠B, ∴∠BEO=∠2, ∴∠1=∠BEO, ∴∠AEC=∠BED 在△AEC和△BED中, ∴△AEC≌△BED. (2)由(1)知△AEC≌△BED, ∴EC=ED,∠C=∠BDE. 又∵∠1=42°, ∴∠C=∠EDC=69°, ∴∠BDE=∠C=69°.
19 连接AD. 在△ABD和△ACD中, ∴△ABD≌△ACD(S.S.S), ∴∠ACD=∠ABD, ∴∠DCF=∠DBE. 又∵∠DFC=∠DEB=90°,DC=DB. ∴△DFC≌△DEB(A.A.S),∴DE=DF.
20 ∵AC⊥BC,AD⊥BD, ∴△ABC和△ABD均是直角三角形. 在Rt△ABC和Rt△BAD中, ∴Rt△ABC≌Rt△BAD(H.L.), ∴AC=BD,∠CAB=∠DBA. ∴△ACE≌△BDF(A.A.S.), ∴DE=DF.
21 (1)∵AB=AC, ∴∠ABC=∠ACB, ∵BD,CE是△ABC的两条高, ∴∠BEC=∠CDB=90°, 又∵BC=CB, ∴△BEC≌△CDB(A.A.S.), ∴∠DBC=∠ECB, ∴OB=OC. (2)∵∠ABC=50°,AB=AC, ∴∠A=180°-2×50°=80°, ∵∠DOE+∠A=180°, ∴∠DOE=180°-∠A=180°-80°=100°, ∴∠BOC=∠DOE=100°.
22 (1)CF=BN.理由如下: 如图,连接CD,DB, ∵AD平分∠CAB,DF⊥AC,DM⊥AB, ∴DF=DM. ∵DE垂直平分BC, ∴CD=BD. 又∵∠CFD=∠DMB=90°, ∴Rt△CDF≌Rt△BDM, ∴CF=BM. (2)∵AD=AD,DF=DM,∠AFD=∠AMD=90°, ∴Rt△AFD≌Rt△AMD, ∴AF=AM. ∵AB=AM+BM,AF=AC+CF,AF=AM,BM=CF, ∴AB=AC+2CF, ∴AB-AC=2CF.
23 【问题提出】 由旋转的性质知BE=AF,∠ABC=∠FAC,EC=FC,∠ECF=60°, ∴△ECF是等边三角形,∴∠FEC=60°, ∴∠AEF+∠BEC=120°. ∵△ABC是等边三角形,∴∠BAC=∠ABC=60°, ∴∠BEC+∠BCE=120°, ∴∠AEF=∠BCE. ∵ED=EC,∴∠D=∠ECD, ∴∠AEF=∠D. ∵∠FAC=60°,∠BAC=60°,∴∠EAF=120°. ∵∠ABC=60°,∴∠DBE=120°,∴∠EAF=∠DBE. 在△AEF和△BDE中, ∵∠AEF=∠BDE,∠EAF=∠DBE,AF=BE, ∴△AEF≌△BDE(A.A.S.),∴AB=DB+AF. 【类比探究】 (1)AB=DB-AF.理由如下: 由旋转的性质知BE=AF,∠EBC=∠FAC,EC=FC,∠ECF=60°,∴△ECF是等边三角形。 ∴∠FEC=60°,∴∠FEA+∠BEC=60°, ∵△ABC是等边三角形,∴∠BAC=∠ABC=60°, ∴∠BEC+∠BCE=60°,∴∠FEA=∠BCE. ∵DE=CE,∴∠D=∠BCE,∴∠FEA=∠D. ∵∠ABC=60°,∴∠DBE=60°,∠EBC=120°, ∴∠FAC=∠EBC=120° 在△AEF和△BDE中, ∵∠FEA=∠EDB,∠FAE=∠EBD,AF=BE, ∴△AEF≌△BDE(A.A.S.),∴AE=BD. ∵AB=AE-BE,AF=BE,AE=BD,∴AB=DB-AF. (2)AB=AF-DB. 只画出图1、图2中的一个图即可。
