沪科版八年级上数学册《第12章一次函数》单元测试题含答案
文档属性
| 名称 | 沪科版八年级上数学册《第12章一次函数》单元测试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 103.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-11 22:07:47 | ||
图片预览



文档简介
第12章 一次函数 单元测试
一、选择题
1.在某个变化过程中,数值保持不变的量,叫做( )
A.?函数????????????????????????????????????B.?变量????????????????????????????????????C.?常量????????????????????????????????????D.?自变量
【答案】C
2.当x=0时,函数y=2x2+1的值是( )
A.?1???????????????????????????????????????????B.?0???????????????????????????????????????????C.?3???????????????????????????????????????????D.?-1
【答案】A
3.在函数y=中,自变量x的取值范围是( )
A.?x>0?????????????????????????????????????B.?x≠0?????????????????????????????????????C.?x>1?????????????????????????????????????D.?x≠1
【答案】B
4.一次函数 的图象不经过的象限是(??? ).
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
【答案】D
5.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量( )
A.?20kg???????????????????????????????????B.?25kg???????????????????????????????????C.?28kg???????????????????????????????????D.?30kg
【答案】A
6.当x>0时,y与x的函数解析式为y=2x,当x≤0时,y与x的函数解析式为y=﹣2x,则在同一直角坐标系中的图象大致为( )
A.????????????B.????????????C.????????????D.?
【答案】C
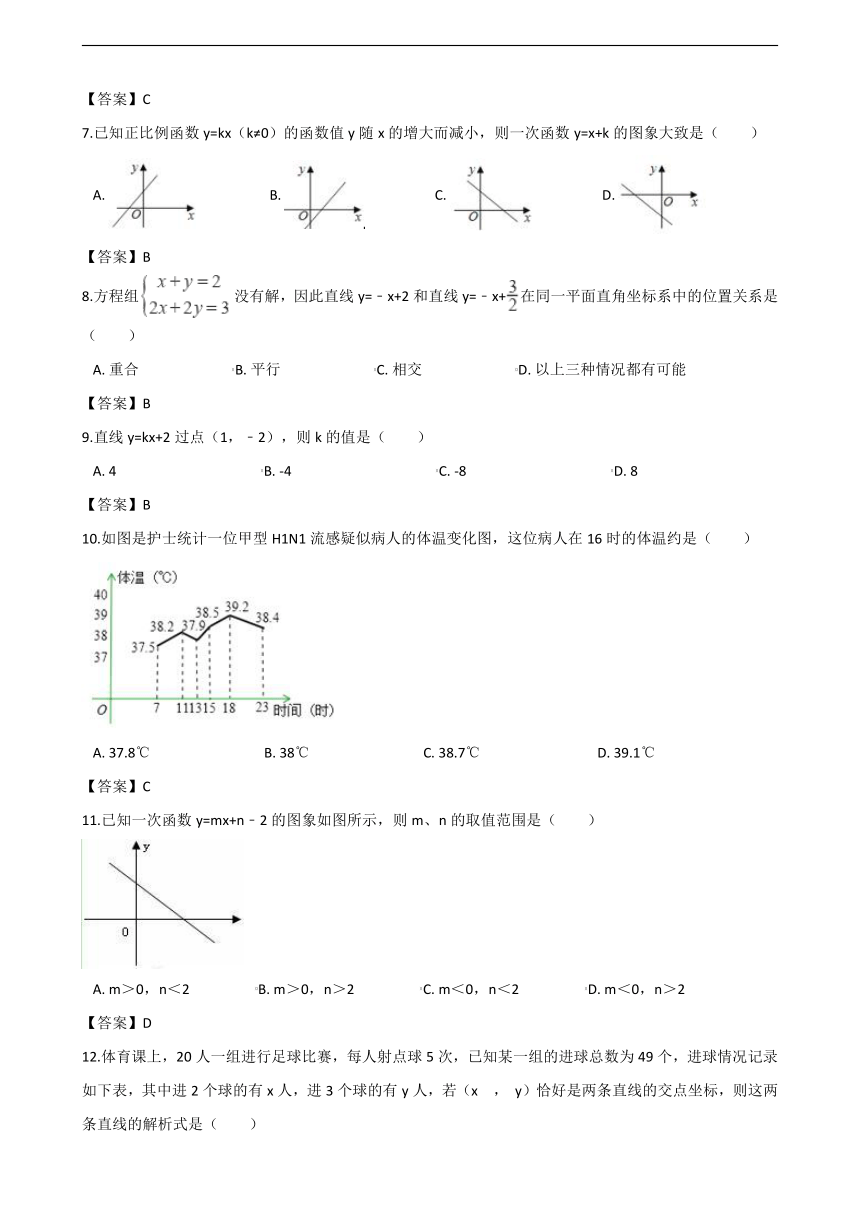
7.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是( )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
【答案】B
8.方程组没有解,因此直线y=﹣x+2和直线y=﹣x+在同一平面直角坐标系中的位置关系是( )
A.?重合???????????????????????????B.?平行???????????????????????????C.?相交???????????????????????????D.?以上三种情况都有可能
【答案】B
9.直线y=kx+2过点(1,﹣2),则k的值是( )
A.?4??????????????????????????????????????????B.?-4??????????????????????????????????????????C.?-8??????????????????????????????????????????D.?8
【答案】B
10.如图是护士统计一位甲型H1N1流感疑似病人的体温变化图,这位病人在16时的体温约是( )
A.?37.8℃?????????????????????????????????B.?38℃?????????????????????????????????C.?38.7℃??????????????????????????????????D.?39.1℃
【答案】C
11.已知一次函数y=mx+n﹣2的图象如图所示,则m、n的取值范围是( )
A.?m>0,n<2???????????????????B.?m>0,n>2???????????????????C.?m<0,n<2???????????????????D.?m<0,n>2
【答案】D
12.体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x , y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )
??? 进球数
?????? 0
?????? 1
??????? 2
?????? 3
?????? 4
?????? 5
???? 人数
?????? 1
?????? 5
??????? x
?????? y
?????? 3
??????? 2
A.??与???????????????????????????????????B.??与 C.?与???????????????????????????????D.?与
【答案】C
二、填空题
13.若函数y= 有意义,则自变量x的取值范围是________.
【答案】x≠
14.若四条直线x=1,y=﹣1,y=3,y=kx﹣3所围成的凸四边形的面积等于12,则k的值为________?
【答案】﹣2或1.
15.设一次函数y=kx+2k-3(k≠0),对于任意两个k的值k1,k2,分别对应两个一次函数值y1,y2,若k1k2<0,当x=m时,取相应y1,y2,中的较小值p,则p的最大值是________.
【答案】-3
16.如图,正比例函数y=kx , y=mx , y=nx在同一平面直角坐标系中的图象如图所示.则比例系数k , m , n的大小关系是________.
【答案】k>m>n
17.若一次函数的图象如图所示,则此一次函数的解析式为________.
【答案】y=-2x-4
18.一次函数y=2x﹣5与y=3x+b的图象的交点为P(1,﹣3),方程组 的解为________,b=________.
【答案】;﹣6
19. 已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则 的值为________.
【答案】﹣
三、解答题
20.已知y+a与x+b(a、b为常数)成正比例. (1)y是x的一次函数吗?请说明理由; (2)在什么条件下y是x的正比例函数.
【答案】解:(1)∵y+a与x+b成正比例, 设比例系数为k,则y+a=k(x+b), 整理得:y=kx+kb﹣a, ∴y是x的一次函数; (2)∵y=kx+kb﹣a, ∴要想y是x的正比例函数, kb﹣a=0即a=kb时y是x的正比例函数.
21.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元. (1)甲、乙两种材料每千克分别是多少元? (2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案? (3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.
【答案】解:(1)设甲种材料每千克x元,乙种材料每千克y元, 依题意得:, 解得:; 答:甲种材料每千克25元,乙种材料每千克35元. (2)设生产B产品a件,生产A产品(60﹣a)件. 依题意得:, 解得:38<a≤; ∵a的值为非负整数, ∴a=39、40、41、42; 答:共有如下四种方案: (3)生产A产品21件,B产品39件成本最低.理由如下: 设生产成本为W元,则W与a的关系式为: W=(25×4+35×1+40)(60﹣a)+(35×3+25×3+50)a=55a+10 500, 即W是a的一次函数, ∵k=55>0 ∴W随a增大而增大 ∴当a=39时,总成本最低; 即生产A产品21件,B产品39件成本最低.
22.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).①求b的值;②不解关于x , y的方程组 ,请你直接写出它的解; ③直线l3:y=nx+m是否也经过点P?请说明理由.
【答案】解:①∵(1,b)在直线y=x+1上,∴当x=1时,b=1+1=2;②方程组的解是? ;③直线y=nx+m也经过点P . 理由如下:∵当x=1时,y=nx+m=m+n=2,∴(1,2)满足函数y=nx+m的解析式,则直线经过点P.
四、综合题
23. 赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
【答案】(1)解:由图可得,起点A与终点B之间相距3000米; (2)解:由图可得,甲龙舟队先出发,乙龙舟队先到达终点; (3)解:设甲龙舟队的y与x函数关系式为y=kx, 把(25,3000)代入,可得3000=25k, 解得k=120, ∴甲龙舟队的y与x函数关系式为y=120x(0≤x≤25), 设乙龙舟队的y与x函数关系式为y=ax+b, 把(5,0),(20,3000)代入,可得 , 解得 , ∴乙龙舟队的y与x函数关系式为y=200x﹣1000(5≤x≤20); (4)解:令120x=200x﹣1000,可得x=12.5, 即当x=12.5时,两龙舟队相遇, 当x<5时,令120x=200,则x= (符合题意); 当5≤x<12.5时,令120x﹣(200x﹣1000)=200,则x=10(符合题意); 当12.5<x≤20时,令200x﹣1000﹣120x=200,则x=15(符合题意); 当20<x≤25时,令3000﹣120x=200,则x= (符合题意); 综上所述,甲龙舟队出发 或10或15或 分钟时,两支龙舟队相距200米
24.一次函数y=﹣ x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
(1)求△ABC的面积和点C的坐标;
(2)如果在第二象限内有一点P(a, ),试用含a的代数式表示四边形ABPO的面积.
(3)在x轴上是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)解:y=﹣ x+1与x轴、y轴交于A、B两点, ∴A( ,0),B(0,1). ∵△AOB为直角三角形, ∴AB=2. ∴S△ABC= ×2×sin60°= . ∵A( ,0),B(0,1). ∴OA= ,OB=1, ∴tan∠OAB= = , ∴∠OAB=30°, ∵∠BAC=60°, ∴∠OAC=90°, ∴C(1,2) (2)解:如图1, S四边形ABPO=S△ABO+S△BOP= ×OA×OB+ ×OB×h= × ×1+ ×1×|a|= + a. ∵P在第二象限, ∴a<0 ∴S四边形ABPO= ﹣ = (3)解:如图2, 设点M(m,0), ∵A( ,0),B(0,1). ∴AM2=(m﹣ )2 , MB2=m2+1,AB=2, ∵△MAB为等腰三角形, ∴①MA=MB, ∴MA2=MB2 , ∴(m﹣ )2=m2+1, ∴m= , ∴M( ,0) ②MA=AB, ∴MA2=AB2 , ∴(m﹣ )2=4, ∴m= ±2, ∴M( +2,0)或( ﹣2,0) ③MB=AB, ∴MB2=AB2 , ∴m2+1=4, ∴m= (舍)或m=﹣ . ∴M(﹣ ,0). ∴满足条件的M的坐标为( ,0)、( +2,0)、( ﹣2,0)、(﹣ ,0)
