沪科版八年级上数学册《第14章全等三角形》单元测试题含答案
文档属性
| 名称 | 沪科版八年级上数学册《第14章全等三角形》单元测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-11 22:19:56 | ||
图片预览



文档简介
第14章 全等三角形 单元测试
一、选择题
1.如图,两个三角形全等,则∠a度数是(?????)
A.?72°???????????????????????????????????????B.?60°???????????????????????????????????????C.?58°???????????????????????????????????????D.?50°
【答案】D
2.已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为?(??)
A.?80°??????????????????????????????????????B.?70°??????????????????????????????????????C.?30°??????????????????????????????????????D.?100°
【答案】A
3.已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为(?? )
A.?2?????????????????????????????????????????B.?3?????????????????????????????????????????C.?4?????????????????????????????????????????D.?不确定
【答案】A
4. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.?∠B=∠C??????????????????????????????B.?AD=AE??????????????????????????????C.?BD=CE??????????????????????????????D.?BE=CD
【答案】D
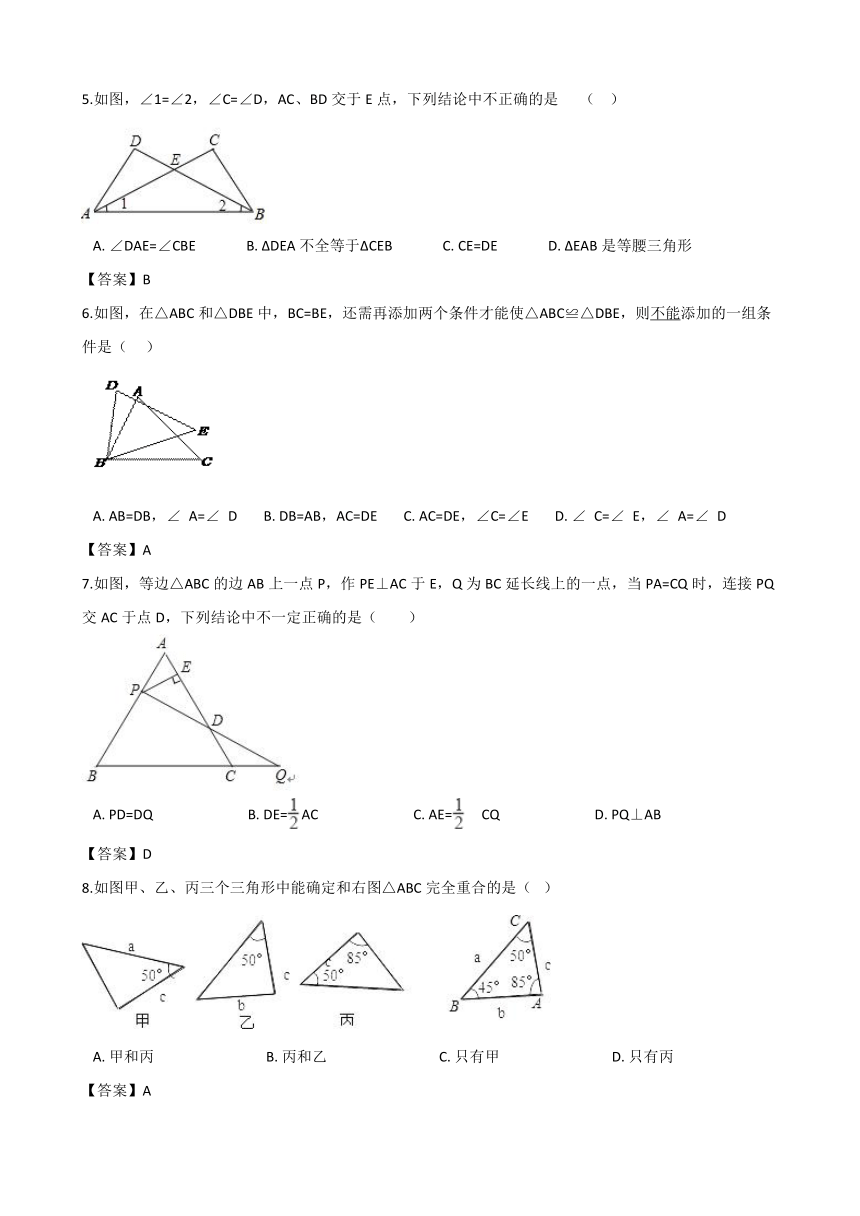
5.如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是???? (?? )
A.?∠DAE=∠CBE??????????????B.?ΔDEA不全等于ΔCEB??????????????C.?CE=DE??????????????D.?ΔEAB是等腰三角形
【答案】B
6.如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是(??? ) ?
A.?AB=DB,∠ A=∠ D???????B.?DB=AB,AC=DE???????C.?AC=DE,∠C=∠E???????D.?∠ C=∠ E,∠ A=∠ D
【答案】A
7.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
A.?PD=DQ???????????????????????????B.?DE=AC???????????????????????????C.?AE=?CQ???????????????????????????D.?PQ⊥AB
【答案】D
8.如图甲、乙、丙三个三角形中能确定和右图△ABC完全重合的是(? )
A.?甲和丙????????????????????????????????B.?丙和乙????????????????????????????????C.?只有甲????????????????????????????????D.?只有丙
【答案】A
9.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
A.?65°??????????????????????????????????????B.?95°??????????????????????????????????????C.?45°??????????????????????????????????????D.?100°
【答案】B
10.如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为( )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?35°???????????????????????????????????????D.?40°
【答案】B
11.下列是利用了三角形的稳定性的有( )个 ①自行车的三角形车架; ②长方形门框的斜拉条; ③照相机的三脚架; ④塔吊上部的三角形结构.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
【答案】D
12.在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
A.?△ACF??????????????????????????????????B.?△ACE??????????????????????????????????C.?△ABD??????????????????????????????????D.?△CEF
【答案】C
二、填空题
13.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有________?性.
【答案】稳定
14.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是________?.
【答案】三角形的稳定性
15.如图,AB∥CD,AC⊥BC,垂足为C.若∠A=40°,则∠BCD=________?度. ?
【答案】50
16.如图,已知AB=DE,BC=EF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:?________ ?
【答案】AC=DF
17. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于________.
【答案】2
18.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=________?度
【答案】90
19.如图,在Rt△ABC和Rt△DCB中,AB=DC , ∠A=∠D=90°,AC与BD交于点O , 则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
【答案】ABC;DCB;HL;AOB;DOC;AAS
三、解答题
20.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC. ?
【答案】证明:∵∠A=∠D=90°,AC=BD,BC=BC, ∴Rt△BAC≌Rt△CDB(HL) ∴∠ACB=∠DBC. ∴∠OCB=∠OBC. ∴OB=OC(等角对等边).
21.如图,点A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
【答案】证明:∵AC=BD, ∴AC+CD=BD+CD, ∴AD=BC, 在△AED和△BFC中, , ∴△AED≌△BFC(ASA), ∴DE=CF
22.已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
【答案】证明:连接AC,AD, 在△ABC与△AED中, ∴△ABC≌△AED, ∴AC=AD, ∵AF⊥CD, ∴CF=DF.
23.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接ME.试判断ME与BC是否垂直,并说明理由.
【答案】(1)证明:∵∠BAC=90°,AF⊥AE, ∴∠1+∠EAC=90°,∠2+∠EAC=90° ∴∠1=∠2, 又∵AB=AC, ∴∠B=∠ACB=45°, ∵FC⊥BC, ∴∠FCA=90°﹣∠ACB=90°﹣45°=45°, ∴∠B=∠FCA, 在△ABE和△ACF中, ?, ∴△ABE≌△ACF(ASA), ∴BE=CF; (2)解:如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形, ∴HE=BH,∠BEH=45°, ∵AE平分∠BAD,AD⊥BC, ∴DE=HE, ∴DE=BH=HE, ∵BM=2DE, ∴HE=HM, ∴△HEM是等腰直角三角形, ∴∠MEH=45°, ∴∠BEM=45°+45°=90°, ∴ME⊥BC.
24.阅读
(1)阅读理解: 如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围. 解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断. 中线AD的取值范围是________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展: 如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】(1)2<AD<8 (2)解:证明:延长FD至点M,使DM=DF,连接BM,EM,如图②所示: 同(1)得:△BMD≌△CFD(SAS), ∴BM=CF, ∵DE⊥DF,DM=DF, ∴EM=EF, 在△BME中,由三角形的三边关系得:BE+BM>EM, ∴BE+CF>EF (3)解:BE+DF=EF;理由如下: 延长AB至点N,使BN=DF,连接CN,如图3所示: ∵∠ABC+∠D=180°,∠NBC+∠ABC=180°, ∴∠NBC=∠D, 在△NBC和△FDC中, , ∴△NBC≌△FDC(SAS), ∴CN=CF,∠NCB=∠FCD, ∵∠BCD=140°,∠ECF=70°, ∴∠BCE+∠FCD=70°, ∴∠ECN=70°=∠ECF, 在△NCE和△FCE中, , ∴△NCE≌△FCE(SAS), ∴EN=EF, ∵BE+BN=EN, ∴BE+DF=EF
