人教A版2003课标高中数学必修1第三章3.1.1方程的 根与函数的零点
文档属性
| 名称 | 人教A版2003课标高中数学必修1第三章3.1.1方程的 根与函数的零点 |  | |
| 格式 | zip | ||
| 文件大小 | 935.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-13 21:24:35 | ||
图片预览






文档简介
课件18张PPT。方程的根与函数的零点华罗庚说:
“数缺形时少直观,
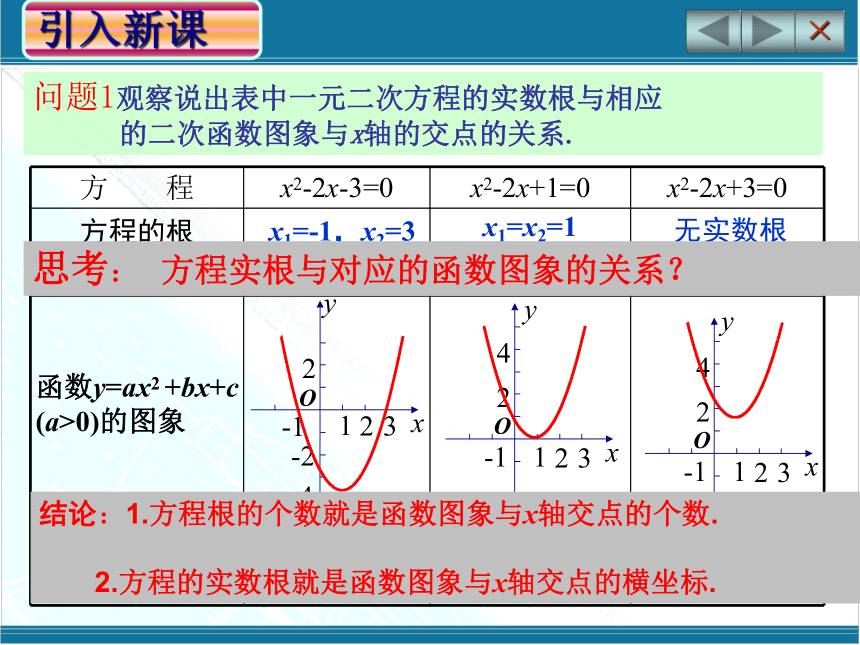
形缺数时难入微”【引例】 解方程 引入新课 问题1观察说出表中一元二次方程的实数根与相应
的二次函数图象与x轴的交点的关系.x1=-1,x2=3x1=x2=1无实数根两个交点
(-1,0),(3,0)一个交点
(1,0)没有交点思考: 方程实根与对应的函数图象的关系?×结论:1.方程根的个数就是函数图象与x轴交点的个数.
2.方程的实数根就是函数图象与x轴交点的横坐标.引入新课 问题2 若将上面特殊的一元二次方程推广到一般的一元二次方程ax2+bx+c=0(a≠0)及相应的二次函数y= ax2+bx+c(a≠0)的图象与x轴交点
的关系,上述结论是否仍然成立?x1=-1,x2=3x1=x2=1无实数根两个交点
(-1,0),(3,0)一个交点
(1,0)没有交点判别式ΔΔ> 0Δ= 0Δ< 0方程ax2 +bx+c=0
(a>0)的根两个不相等的
实数根x1 、x2有两个相等的
实数根x1 = x2没有实数根x1x2x1(x1,0), (x2,0)(x1,0)结论:1.方程根的个数就是函数图象与x轴交点的个数.
2.方程的实数根就是函数图象与x轴交点的横坐标.×函数零点的定义 等价关系: 方程f(x)=0有实数根
? 函数y=f(x)的图像与x轴有交点
? 函数y=f(x)有零点
问题3 函数的零点与方程的根有什么联系? 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点.× 注意:零点是自变量的值,而不是一个点.3,- 3函数零点的定义 D×求函数零点的步骤:
(1)令f(x)=0 (2)解方程f(x)=0 (3)写出零点.??第1组第2组探究3 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河? ??函数零点存在性的探究 观察二次函数f(x)=x2-2x-3的图象:
在区间(-2, 1)上有零点______;
f(-2)=_______,f(1)=_______,
f(-2)·f(1)_____0(“<”或“>”).
在区间(2,4)上有零点______;
f(2)=_______,f(4)=_______,
f(2)·f(4)____0(“<”或“>”). 探究: 问题4:在怎样的条件下,函数y=f(x)在区间(a,b)上存在零点? -1-45<3<-35×问题5:在怎样的条件下,函数y=f(x)在区间(a,b)上存在零点? 观察函数的图象并填空:
①在区间[a,b]上f(a)·f(b)_____0(“<”或“>”).
在区间(a,b)上______(有/无)零点;
② 在区间[b,c]上f(b)·f(c) _____ 0(“<”或“>”).
在区间(b,c)上______(有/无)零点;
③ 在区间[c,d]上f(c)·f(d) _____ 0(“<”或” >”).
在区间(c,d)上______(有/无)零点;有<有<有 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.函数零点存在性定理 × 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.函数零点存在性定理:思考探究:下列判断是否正确,不正确的请画图举出反例。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(3)已知函数y=f (x)在区间[a,b] 满足f (a) ·f(b) < 0,则f(x)在区间(a,b)内存在零点. ( )×思考探究:下列判断是否正确,不正确的请画图举出反例。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(3)已知函数y=f (x)在区间[a,b] 满足f (a) ·f(b) < 0,则f(x)在区间(a,b)内存在零点. ( )图1图2图3×由表可知f(2)<0,f(3)>0,从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.由于函数y=lnx和y=2x-6在定义域 (0,+∞)内是增函数, 所以函数f(x)在定义域(0,+∞)内是增函数,因此它仅有一个零点.用计算器或计算机作出x、f(x)的对应值表:解法1: 零点存在性定理的应用:问题6:如何说明零点的唯一性? -1.30691.09863.38637.79189.945912.079414.1972f(x)=lnx+2x- 6-4例1 求函数f(x)=lnx+2x- 6的零点的个数,并确定零点所在的区间[n, n+1] (n∈Z) .×5.6094解法2:估算f(x)在各整数处的取值的正负:解法3:将函数f(x)= lnx+2x-6的零点的个数转化为函数 y= lnx与y=-2x +6的图象交点的个数.y=-2x +6y= lnx例1 求函数f(x)=lnx+2x-6 的零点的个数,并确定零点所在的区间[n, n+1](n∈Z) .- + 零点存在性定理的应用:× +- 但在确定区间的时候,由于画图,不够精确,容易带来错误,所以多用在判断零点个数上. 那么函数在区间[1, 6]上的零点至少有( )个
A. 5个 B. 4个 C. 3个 D. 2个
2、函数f (x)= – x 3 – 3x + 5的零点所在的大致区间为( )
A. ( – 2 ,0) B. (1,2) C. (0,1) D. (0,0.5) CB1、已知函数f (x)的图象是连续不断的,有如下对应值表:零点存在性定理的应用:×函数零点与方程根的关系:函数方程零点根函数方程思想;数形结合思想. 求函数零点、确定零点个数、
求零点所在区间. 课堂小结 ×一个关系:三种题型:两种思想:数学日记——年——月——日 星期——天气——
“数缺形时少直观,
形缺数时难入微”【引例】 解方程 引入新课 问题1观察说出表中一元二次方程的实数根与相应
的二次函数图象与x轴的交点的关系.x1=-1,x2=3x1=x2=1无实数根两个交点
(-1,0),(3,0)一个交点
(1,0)没有交点思考: 方程实根与对应的函数图象的关系?×结论:1.方程根的个数就是函数图象与x轴交点的个数.
2.方程的实数根就是函数图象与x轴交点的横坐标.引入新课 问题2 若将上面特殊的一元二次方程推广到一般的一元二次方程ax2+bx+c=0(a≠0)及相应的二次函数y= ax2+bx+c(a≠0)的图象与x轴交点
的关系,上述结论是否仍然成立?x1=-1,x2=3x1=x2=1无实数根两个交点
(-1,0),(3,0)一个交点
(1,0)没有交点判别式ΔΔ> 0Δ= 0Δ< 0方程ax2 +bx+c=0
(a>0)的根两个不相等的
实数根x1 、x2有两个相等的
实数根x1 = x2没有实数根x1x2x1(x1,0), (x2,0)(x1,0)结论:1.方程根的个数就是函数图象与x轴交点的个数.
2.方程的实数根就是函数图象与x轴交点的横坐标.×函数零点的定义 等价关系: 方程f(x)=0有实数根
? 函数y=f(x)的图像与x轴有交点
? 函数y=f(x)有零点
问题3 函数的零点与方程的根有什么联系? 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点.× 注意:零点是自变量的值,而不是一个点.3,- 3函数零点的定义 D×求函数零点的步骤:
(1)令f(x)=0 (2)解方程f(x)=0 (3)写出零点.??第1组第2组探究3 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河? ??函数零点存在性的探究 观察二次函数f(x)=x2-2x-3的图象:
在区间(-2, 1)上有零点______;
f(-2)=_______,f(1)=_______,
f(-2)·f(1)_____0(“<”或“>”).
在区间(2,4)上有零点______;
f(2)=_______,f(4)=_______,
f(2)·f(4)____0(“<”或“>”). 探究: 问题4:在怎样的条件下,函数y=f(x)在区间(a,b)上存在零点? -1-45<3<-35×问题5:在怎样的条件下,函数y=f(x)在区间(a,b)上存在零点? 观察函数的图象并填空:
①在区间[a,b]上f(a)·f(b)_____0(“<”或“>”).
在区间(a,b)上______(有/无)零点;
② 在区间[b,c]上f(b)·f(c) _____ 0(“<”或“>”).
在区间(b,c)上______(有/无)零点;
③ 在区间[c,d]上f(c)·f(d) _____ 0(“<”或” >”).
在区间(c,d)上______(有/无)零点;有<有<有
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.函数零点存在性定理:思考探究:下列判断是否正确,不正确的请画图举出反例。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(3)已知函数y=f (x)在区间[a,b] 满足f (a) ·f(b) < 0,则f(x)在区间(a,b)内存在零点. ( )×思考探究:下列判断是否正确,不正确的请画图举出反例。
(1)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) < 0,则f(x)在区间(a,b)内有且仅有一个零点. ( )
(2)已知函数y=f (x)在区间[a,b]上连续,且f (a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
(3)已知函数y=f (x)在区间[a,b] 满足f (a) ·f(b) < 0,则f(x)在区间(a,b)内存在零点. ( )图1图2图3×由表可知f(2)<0,f(3)>0,从而f(2)·f(3)<0,
∴函数f(x)在区间(2,3)内有零点.由于函数y=lnx和y=2x-6在定义域 (0,+∞)内是增函数, 所以函数f(x)在定义域(0,+∞)内是增函数,因此它仅有一个零点.用计算器或计算机作出x、f(x)的对应值表:解法1: 零点存在性定理的应用:问题6:如何说明零点的唯一性? -1.30691.09863.38637.79189.945912.079414.1972f(x)=lnx+2x- 6-4例1 求函数f(x)=lnx+2x- 6的零点的个数,并确定零点所在的区间[n, n+1] (n∈Z) .×5.6094解法2:估算f(x)在各整数处的取值的正负:解法3:将函数f(x)= lnx+2x-6的零点的个数转化为函数 y= lnx与y=-2x +6的图象交点的个数.y=-2x +6y= lnx例1 求函数f(x)=lnx+2x-6 的零点的个数,并确定零点所在的区间[n, n+1](n∈Z) .- + 零点存在性定理的应用:× +- 但在确定区间的时候,由于画图,不够精确,容易带来错误,所以多用在判断零点个数上. 那么函数在区间[1, 6]上的零点至少有( )个
A. 5个 B. 4个 C. 3个 D. 2个
2、函数f (x)= – x 3 – 3x + 5的零点所在的大致区间为( )
A. ( – 2 ,0) B. (1,2) C. (0,1) D. (0,0.5) CB1、已知函数f (x)的图象是连续不断的,有如下对应值表:零点存在性定理的应用:×函数零点与方程根的关系:函数方程零点根函数方程思想;数形结合思想. 求函数零点、确定零点个数、
求零点所在区间. 课堂小结 ×一个关系:三种题型:两种思想:数学日记——年——月——日 星期——天气——
