人教A版2003课标高中数学必修1第三章3.1.1方程的根与函数的零点
文档属性
| 名称 | 人教A版2003课标高中数学必修1第三章3.1.1方程的根与函数的零点 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-13 00:00:00 | ||
图片预览






文档简介
课件22张PPT。高一数学人教A版必修1§3.1.1 方程的根与函数的零点解方程:①②③〖引例〗1.理解函数零点的概念,掌握函数
零点的求法(重点);
2.领会函数零点与相应方程的根及
函数的图象与x轴的交点三者之
间的的等价关系(重点);
3.掌握零点存在性定理及其拓展
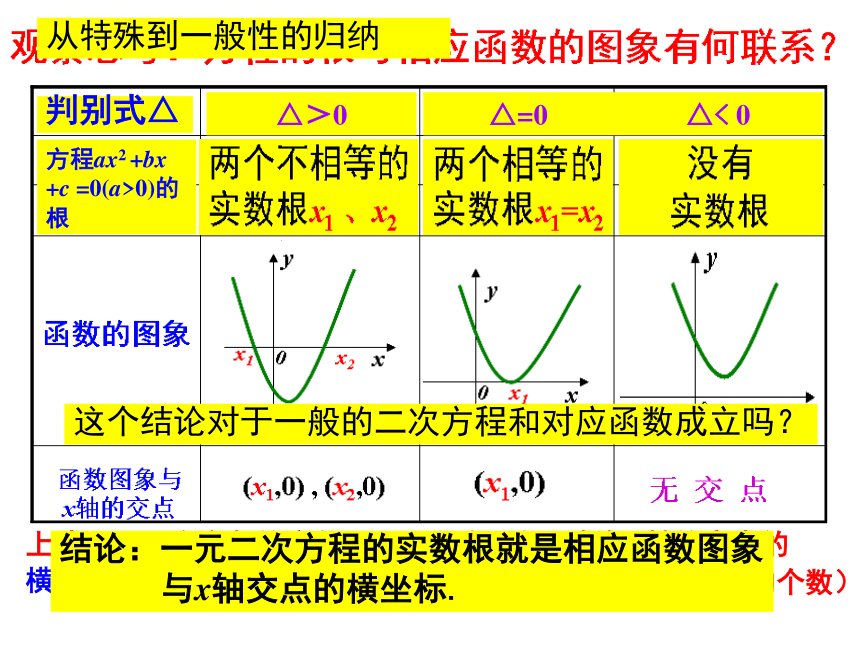
应用(难点).【学习目标】判别式△方程ax2 +bx
+c =0(a>0)的根△>0△=0△< 0这个结论对于一般的二次方程和对应函数成立吗?从特殊到一般性的归纳结论:一元二次方程的实数根就是相应函数图象
与x轴交点的横坐标.③ 对于函数 y = f(x) ,使 f(x) = 0 的实数x叫做函数的零点.方程f(x)=0的实数根函数y=f(x)的图象与x轴的交点的横坐标函数y=f(x)的零点等价关系探究二:函数零点的等价关系小惊喜:探求函数y=f(x)的零点的两条途径.练一练已知偶函数
在 时的图象
如图所示,则此函数零点
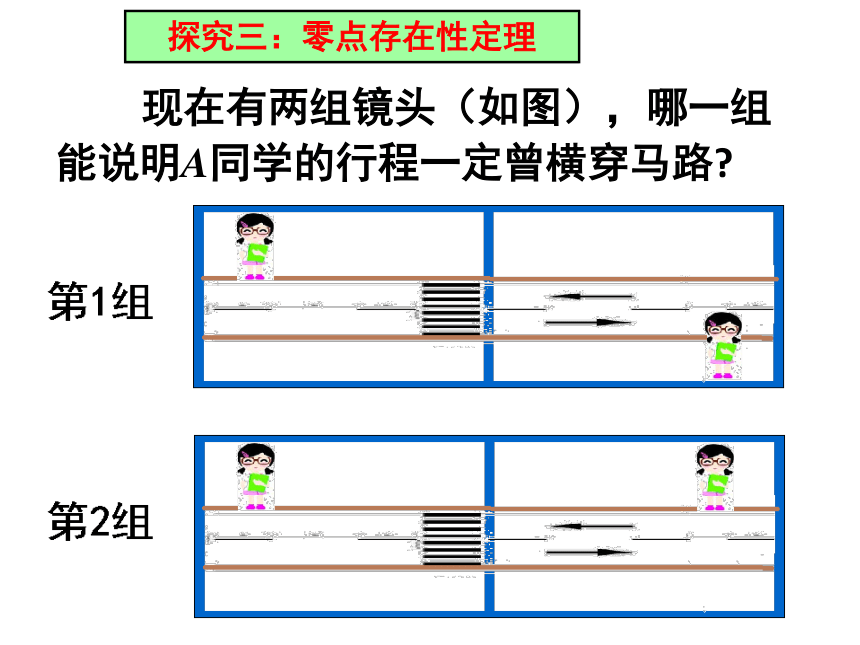
的个数是______.⒈4思考:是否所有的函数都有零点呢? 现在有两组镜头(如图),哪一组
能说明A同学的行程一定曾横穿马路? ??探究三:零点存在性定理 第1组情况,若将马路抽象成 x 轴,前后的两个位置视为A、B两点.请用连
续不断的曲线画出她的可能路径.
探究三:零点存在性定理 若所画曲线能表示函数的图象,设A点横坐标为a,B点横坐标为b,问:函数在区间(a,b)内一定存在零点吗?探究三:零点存在性定理 若函数的图象不是连续不断的,函数一定存在零点吗?探究三:零点存在性定理探究三:零点存在性定理 如果函数y=f(x)在区间[a,b]上的图象
是________的一条曲线,并且有f(a)·f(b)__0,那么,函数y=f(x)在区间(a,b) 内有零点. 即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根.探究三:零点存在性定理?探究三:零点存在性定理(若不成立,利用图象举出反例) c学会了吗? ..B 如果函数y=f(x)在区间[a,b]上的图象
是连续不断的一条曲线,并且有 f(a)·f(b)<0,
那么,函数y=f(x)在区间(a,b)
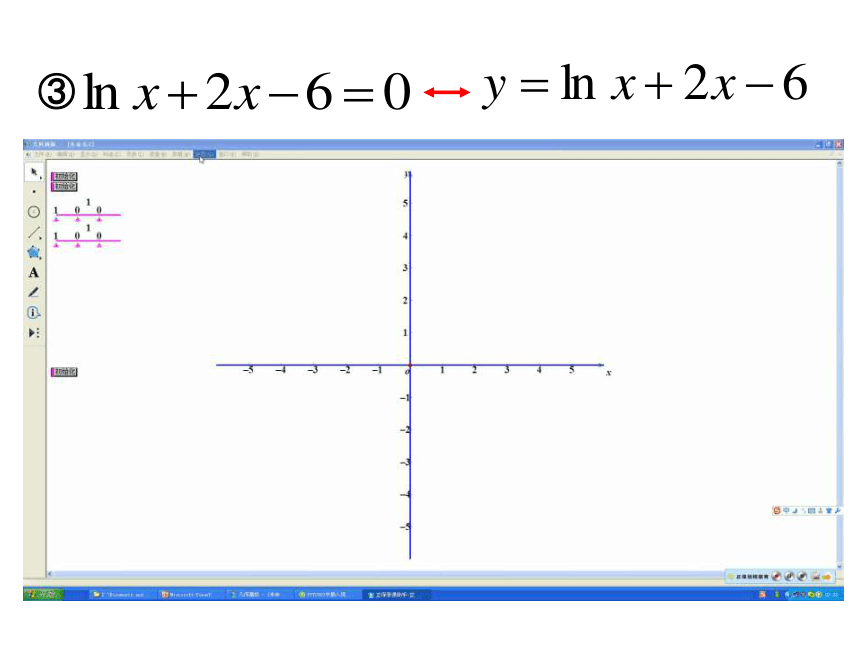
内有零点.给定理增加什么条件时,函数在区间(a,b)上只有一个零点?探究四:零点存在性定理的拓展零点存在性定理的应用 例.判断函数 f (x) = lnx + 2x – 6是否有零点,如果有,
说出零点的个数,如果没有,说明理由.这说明函数f(x)在区间(2,3)内有零点,由于函数f(x)在定义域(0,+∞)内是增函数,
所以它仅有一个零点.细 数 收 获①函数零点的概念
②等价关系
③函数零点的存在性定理㈠知识点㈡数学思想方法体会函数与方程和数形结合的数学思想记忆口诀:
零点不是点;
等价三相连.
上下不间断;
零点可呈现.?
零点的求法(重点);
2.领会函数零点与相应方程的根及
函数的图象与x轴的交点三者之
间的的等价关系(重点);
3.掌握零点存在性定理及其拓展
应用(难点).【学习目标】判别式△方程ax2 +bx
+c =0(a>0)的根△>0△=0△< 0这个结论对于一般的二次方程和对应函数成立吗?从特殊到一般性的归纳结论:一元二次方程的实数根就是相应函数图象
与x轴交点的横坐标.③ 对于函数 y = f(x) ,使 f(x) = 0 的实数x叫做函数的零点.方程f(x)=0的实数根函数y=f(x)的图象与x轴的交点的横坐标函数y=f(x)的零点等价关系探究二:函数零点的等价关系小惊喜:探求函数y=f(x)的零点的两条途径.练一练已知偶函数
在 时的图象
如图所示,则此函数零点
的个数是______.⒈4思考:是否所有的函数都有零点呢? 现在有两组镜头(如图),哪一组
能说明A同学的行程一定曾横穿马路? ??探究三:零点存在性定理 第1组情况,若将马路抽象成 x 轴,前后的两个位置视为A、B两点.请用连
续不断的曲线画出她的可能路径.
探究三:零点存在性定理 若所画曲线能表示函数的图象,设A点横坐标为a,B点横坐标为b,问:函数在区间(a,b)内一定存在零点吗?探究三:零点存在性定理 若函数的图象不是连续不断的,函数一定存在零点吗?探究三:零点存在性定理探究三:零点存在性定理 如果函数y=f(x)在区间[a,b]上的图象
是________的一条曲线,并且有f(a)·f(b)__0,那么,函数y=f(x)在区间(a,b) 内有零点. 即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根.探究三:零点存在性定理?探究三:零点存在性定理(若不成立,利用图象举出反例) c学会了吗? ..B 如果函数y=f(x)在区间[a,b]上的图象
是连续不断的一条曲线,并且有 f(a)·f(b)<0,
那么,函数y=f(x)在区间(a,b)
内有零点.给定理增加什么条件时,函数在区间(a,b)上只有一个零点?探究四:零点存在性定理的拓展零点存在性定理的应用 例.判断函数 f (x) = lnx + 2x – 6是否有零点,如果有,
说出零点的个数,如果没有,说明理由.这说明函数f(x)在区间(2,3)内有零点,由于函数f(x)在定义域(0,+∞)内是增函数,
所以它仅有一个零点.细 数 收 获①函数零点的概念
②等价关系
③函数零点的存在性定理㈠知识点㈡数学思想方法体会函数与方程和数形结合的数学思想记忆口诀:
零点不是点;
等价三相连.
上下不间断;
零点可呈现.?
