第三讲 圆周运动 万有引力与航天
文档属性
| 名称 | 第三讲 圆周运动 万有引力与航天 |
|
|
| 格式 | rar | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-02-25 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
第三讲 圆周运动 万有引力与航天
HXLRZH 核心内容整合
一、圆周运动
1.描述圆周运动的物理量
物理量 物理意义 大小 方向
线速度 描述质点沿圆周运动的快慢 ν= = 沿圆弧在该点的切线方向
角速度 ω= = 中学不研究其方向
周期、频率 T= = 无方向
向心加速度 描述线速度方向改变的快慢 a = = =ω2r 时刻指向圆心
相互关系 a = =ω2r =4π2f2r= =ωυ
友情提示 在分析传动装置中各物理量时,要抓住相等量和不等量的关系.同轴转动的物体上各点的角速度相等,线速度υ=ωr,与半径r成正比;皮带传动(或齿轮传动)的两轮,在皮带不打滑的条件下,两轮边缘各点的线速度大小相等,角速度ω= ,与半径r成反比.
2.向心力
(1)来源:在匀速圆周运动中,向心力是物体受到的合力;在变速圆周运动中,向心力的大小等于物体受到的沿着半径方向的合力.F径台=F向=ma向.
(2)作用效果:向心力的方向始终指向圆心,与线速度方向垂直,因此它只改变线速度的方向,不改变线速度的大小.
友情提示 解决圆周运动的关键:正确受力分析,进行力的分解(沿法向和切向),建立F供=F需的关系.
3.离心运动
做匀速圆周运动的物体,在所受的合力突然消失时,物体将沿圆周的切线方向飞出做匀速直线运动;在所提供的合力大于所需要的向心力时,物体将做向心运动;在所提供的合力小于所需要的向心力时,物体将做离心运动.
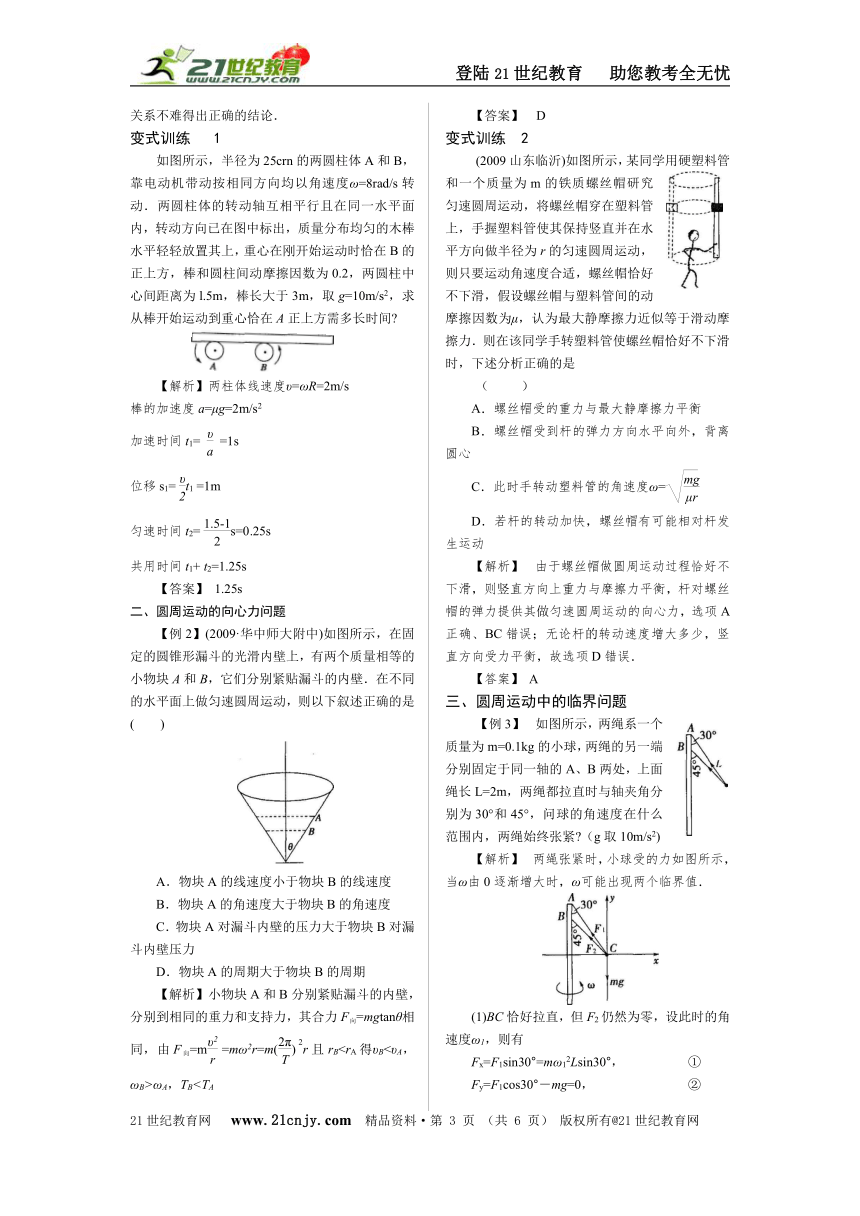
4.竖直面内圆周运动的临界条件
(1)在图甲、乙所示的情景中:
( http: / / www.21cnjy.com )
①当υ= (即mg=m)时,
小球刚好能通过最高点,球和绳(或轨道)之间无相互作用.
②当υ> (即m>mg)时,图甲中绳对小球有向下的拉力,图乙中,轨道对小球有向下的支持力.
③当υ<时,小球不能通过最高点,即在到达最高点之前绳已松弛或球脱离轨道.
(2)在下图甲、乙所示的情景中:
甲 乙
①当υ=0时,轻杆(或内轨)对小球有竖直向上的支持力FN ,其大小等于小球的重力,即FN=mg.
②当0<υ<时,杆(或内轨)对小球的支持力的方向竖直向上,大小随速度的增大而减小,其取值范围是0③当υ=,FN = 0.
④当υ>时,杆(或外轨)对小球有指向圆心的力,其大小随速度的增大而增大,FN >0.
友情提示 (1)对“绳模型”而言,υ=是物体能否通过最高点的临界;对“杆模型”而言υ=是弹力竖直向上还是竖直向下的临界点.
(2)若物体还受到其他恒定的外力,可将该恒力与重力等效为新的“重力” mg' 进行分析,并确定相应的最高点.确定“等效重力”后,可用类比的方法确定其临界条件.
二、万有引力定律的应用
1.万有引力定律:F=G ,G=6.67×10-11 N·m2·kg-2,适用于两质点间的相互作用力.
2.万有引力定律的应用
(1)测天体的质量和密度
①利用天体表面的重力加速度g和天体的半径R.
在天体表面附近G =mg,故M = .
变换可得GM=gR2,称为“黄金代换”.
②利用天体的卫星:已知卫星的周期T(或线速度υ)和卫星的轨道半径r.
G = m = mr等,即可求M.
测天体密度:将M代入ρ= eq \f(M,πR3)即可确定天体的密度.
警示 (1)此方法只能确定中心天体的质量M.
(2)注意区分r的R的不同含义:r为轨道半径,R为天体半径,当卫星在天体表面运行时才有r =R.
(2)分析天体或卫星的运行规律
①把天体或卫星的运动近似看做圆周运动,它所需要的向心力由万有引力提供,即G = m=mrω2= mr=ma向.于是得到υ=eq \r(G),ω=eq \r(G),T=2πeq \r() , a向= G
由此可知:r增大,υ减小,ω减小,T增大,a向减小.
友情提示 (1)以上特点可概括为“越高越慢”.
(2)所有卫星的轨道平面都应过地心,即以地心为轨迹的圆心.
②地球同步卫星:相对于地面静止的人造卫星,它的周期T=24h.所以它只能位于赤道正上方某一确定高度h,h=()+-R≈3.6×104km,但它的质量可以不同.
3.三个宇宙速度
(1)第一宇宙速度υ1=7.9km/s是人造地球卫星的最小发射速度,最大绕行速度.
计算方法:①根据G =m,导出υ=eq \r().
②根据mg = m ,导出υ=.
(2)第二宇宙速度υ2=11.2km/s是物体挣脱地球的引力束缚需要的最小发射速度.
(3)第三宇宙速度υ3=16.7km/s是物体挣脱太阳的引力束缚需要的最小发射速度.
警示 虽然半径越大(离地面越高)的卫星环绕速度越小,但在发射过程中需要克服地球的引力做更多的功,增大势能,所以在地面上的发射速度也就越大,因此,不要认为υ环越小,υ发就越小.
DXLTPX典型例题剖析
一、描述圆周运动的各量之间的关系
【例1】 如图所示,一种向自行车灯供电的小发电机的上端有一半径r0=1.0cm的摩擦小轮,小轮与自行车车轮的边缘接触.当车轮转动时,因摩擦带动小轮转动,从而为发电机提供动力.自行车车轮的半径R1=35cm,小齿轮的半径R2=4.0cm,大齿轮的半径R3=10.0cm.求大齿轮的转速n3和摩擦小轮的转速n0之比.(假定摩擦小轮与自行车轮之间无相对滑动) ( )
( http: / / www.21cnjy.com )
【解析】 根据大、小齿轮两轮边缘各点的线速度大小相等,由υ=2πnR可得:2πn3R 3=2πn2R 2
因为小齿轮和车轮同轴转动,所以两轮上各点的转速相同,故有:n2= n1
小轮与自行车车轮的边缘接触,当车轮转动时,因摩擦而带动小轮转动,且两者无相对滑动,所以它们的线速度相同,则有:2πn1R 1=2πn0r0
由以上各式并代入数据可得大齿轮和摩擦小轮间的转速之比:,n3:n0=2:175.
【答案】 2:175
【总结评述】 凡是直接用皮带传动(包括链条传动、摩擦传动)的两个轮子,在不打滑时两轮边缘上各点的线速度大小相等;凡是同一个轮轴上(各个轮都绕同一根轴同步转动)的各点角速度相等(轴上的点除外).再根据描述圆周运动的各物理量之间的关系不难得出正确的结论.
变式训练 1
如图所示,半径为25crn的两圆柱体A和B,靠电动机带动按相同方向均以角速度ω=8rad/s转动.两圆柱体的转动轴互相平行且在同一水平面内,转动方向已在图中标出,质量分布均匀的木棒水平轻轻放置其上,重心在刚开始运动时恰在B的正上方,棒和圆柱间动摩擦因数为0.2,两圆柱中心间距离为l.5m,棒长大于3m,取g=10m/s2,求从棒开始运动到重心恰在A正上方需多长时间
【解析】两柱体线速度υ=ωR=2m/s
棒的加速度a=μg=2m/s2
加速时间t1= =1s
位移s1= t1 =1m
匀速时间t2= s=0.25s
共用时间t1+ t2=1.25s
【答案】 1.25s
二、圆周运动的向心力问题
【例2】(2009·华中师大附中)如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁.在不同的水平面上做匀速圆周运动,则以下叙述正确的是 ( )
( http: / / www.21cnjy.com )
A.物块A的线速度小于物块B的线速度
B.物块A的角速度大于物块B的角速度
C.物块A对漏斗内壁的压力大于物块B对漏斗内壁压力
D.物块A的周期大于物块B的周期
【解析】小物块A和B分别紧贴漏斗的内壁,分别到相同的重力和支持力,其合力F向=mgtanθ相同,由F向=m =mω2r=m() 2r且rBωA,TB【答案】 D
变式训练 2
(2009山东临沂)如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽穿在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是 ( )
A.螺丝帽受的重力与最大静摩擦力平衡
B.螺丝帽受到杆的弹力方向水平向外,背离圆心
C.此时手转动塑料管的角速度ω=eq \r()
D.若杆的转动加快,螺丝帽有可能相对杆发生运动
【解析】 由于螺丝帽做圆周运动过程恰好不下滑,则竖直方向上重力与摩擦力平衡,杆对螺丝帽的弹力提供其做匀速圆周运动的向心力,选项A正确、BC错误;无论杆的转动速度增大多少,竖直方向受力平衡,故选项D错误.
【答案】 A
三、圆周运动中的临界问题
【例3】 如图所示,两绳系一个质量为m=0.1kg的小球,两绳的另一端分别固定于同一轴的A、B两处,上面绳长L=2m,两绳都拉直时与轴夹角分别为30°和45°,问球的角速度在什么范围内,两绳始终张紧 (g取10m/s2)
【解析】 两绳张紧时,小球受的力如图所示,当ω由0逐渐增大时,ω可能出现两个临界值.
( http: / / www.21cnjy.com )
(1)BC恰好拉直,但F2仍然为零,设此时的角速度ω1,则有
Fx=F1sin30°=mω12Lsin30°, ①
Fy=F1cos30°-mg=0, ②
联立①②代入数据得ω1=2.4rad/s
(2)AC由拉紧转为恰好拉直,但F1已为零,设此时的角速度为ω2,则有
Fx=F2sin45°=mω22Lsin30°, ③
Fy=F2cos45°-mg = 0, ④
联立③④代入已知数据得ω1=3.16rad/s
可见,要使两绳始终张紧,ω必须满足
2.40rad/s≤ω≤3.16rad/s.
【答案】 2.40rad/s≤ω≤3.16rad/s
【总结评述】 (1)要会用极限分析法判定物体可能处的状态,进而正确受力分析.
(2)要注意确定物体做圆周运动的圆心和半径.
(3)只要物体做圆周运动,在任何一个位置和状态,都满足F供=F需,建立该动力学关系是解决圆周运动问题的基本方法.
变式训练 3
(2008·江苏四市联考)如图所示,质量为m的小球置于正方体的光滑硬质盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为尺的匀速圆周运动,已知重力加速度为g,空气阻力不计,问:
( http: / / www.21cnjy.com )
(1)要使盒子在最高点时盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为多少
(2)若盒子以(1)中周期的做匀速圆周运动,则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大
【解析】 (1)设此时盒子的运动周期为T0,因为在最高点时盒子与小球之间刚好无作用力,因此小球仅受重力作用.根据牛顿运动定律得:mg=m,又υ=解得T0=2πeq \r()
(2)设此时盒子的运动周期为T,则此时小球的向心加速度为an=R由(1)知:g=R且T=
由上述三式知:an=4g
设小球受盒子右侧面的作用力为F,受上侧面的作用力为FN,根据牛顿运动定律知:
在水平方向上:F=man=4mg.
在竖直方向上:FN+mg=0,即FN =-mg
因为F为正值、FN为负值,所以小球对盒子的右侧面和下侧面有作用力,分别为4mg和rng.
【答案】 (1) =2πeq \r() (2)对右侧面压力为4mg,对下侧面压力为mg.
四、卫星或天体的运动
【例4】 (2009·四川)据报道,2009年4月29日,美国亚利桑那州一天文观测机构发现一颗与太阳系其它行星逆向运行的小行星,代号为2009HC82.该小行星绕太阳一周的时间为3.39年,直径2~3千米,其轨道平面与地球轨道平面呈l55°的倾斜.假定该小行星与地球均以太阳为中心做匀速圆周运动,则小行星和地球绕太阳运动的速度大小的比值为 ( )
A.3.39- B.3.39-
C.3.39 D.3.39
【解析】 本题考查天体运动问题,由万有引力提供向心力 =m行 =m地
由此可得:υ2行= υ2地= , =eq \r()
同理: = m行r行
= m地r地
将以上两式相比代入可知,A正确,B、C、D错,A正确。
【答案】 A
变式训练 4
(2009·江苏南京)2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空行走标志着中国航天事业全新时代的到来.“神舟七号”绕地球做近似匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为2r,则可以确定 ( )
( http: / / www.21cnjy.com )
A.卫星与“神舟七号”的加速度大小之比为1:4
B.卫星与“神舟七号”的线速度大小之比为1:
C.翟志刚出舱后不再受地球引力
D.翟志刚出舱任务之一是取回外挂的实验样品,假如不小心实验样品脱手,则它做自由落地运动
【解析】 加速度计算公式为a= = ,所以卫星和“神舟七号”的加速度之比为l:4,A选项正确;线速度计算公式为υ=eq \r(),所以卫星和“神舟七号”的线速度之比为l:,B选项正确;翟志刚出舱后依然受到地球的引力,引力提供其做匀速圆周运动所需的向心力,C选项错误;实验样品脱手后,依然做匀速圆周运动,相对飞船静止,D选项错误。
【答案】 AB
五、卫星(或飞行器)的变轨问题
【例5】 (2009·山东)2008年9月25日至28日,我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是 ( )
A.飞船变轨前后的机械能相等
B.飞船在圆轨道上时航天员出舱前后都处于失重状态
C.飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度
D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度
【解析】 本题主要考查向心力及功能关系,飞船变轨时加速外力做功,机械能不守恒,A错,飞船在轨道上运行时万有引力提供向心力处于失重状态,启正确,飞船在此轨道上运行时期为90分钟,小于同步卫星周期,由T= 可知C正确, =ma,可知二者加速度相等,D错,正确答案BC.
【答案】 BC
友情提示 在变轨中不能再利用G =m,生来推导结论,因万有引力恰好等于向心力时,飞船是在圆轨道上行的,而非进行变轨.变轨时应从两方面考虑:一是地球拱的引力F引= ,在开始变轨时F引不变;二是飞船需要的向心力F向=m,可以通过改变飞船的速度来变它所需要的向心力,从而达到使其做向心运动或离心功而变轨的目的.
变式训练 5
(2008·南通调研)如图所示,“嫦娥一号”探月卫星入月球轨道后,首先在椭圆轨道I上运动,P、Q两点是轨道I的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道I和Ⅱ在P点相切,关于探月卫星的运动,下列说正确的是 ( )
( http: / / www.21cnjy.com )
A.卫星在轨道I上运动周期大于在Ⅱ上运动的周期
B.卫星由轨道I进入轨道Ⅱ必须要在P点减速
C.卫星在轨道I上运动时,P点的速度小于Q点的速度
D.卫星在轨道I上运动时,P点的加速度小于Q点的加速度
【解析】 由开普勒第三定律可知,椭圆轨道上,围绕同一中心天体运行的天体,半长轴越长,周期越长,A正确;在P点由轨道l进入轨道Ⅱ时,由于要做近心运动,月球提供的引力不变的情况下,必须使其减速,所需要的向心力变小,才能达到目的,B正确;在同一椭圆轨道上,近月点处速度大于远月点处速度,C错误;近月点万有引力大于在远月点万有引力,向心加速度在近月点处大,D错误.
【答案】 AB
温馨提示:
同学们:针对你们所学内容的巩固与掌握,请认真完成课后强化作业(五)及阶段性测试题(二)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 6 页) 版权所有@21世纪教育网
第三讲 圆周运动 万有引力与航天
HXLRZH 核心内容整合
一、圆周运动
1.描述圆周运动的物理量
物理量 物理意义 大小 方向
线速度 描述质点沿圆周运动的快慢 ν= = 沿圆弧在该点的切线方向
角速度 ω= = 中学不研究其方向
周期、频率 T= = 无方向
向心加速度 描述线速度方向改变的快慢 a = = =ω2r 时刻指向圆心
相互关系 a = =ω2r =4π2f2r= =ωυ
友情提示 在分析传动装置中各物理量时,要抓住相等量和不等量的关系.同轴转动的物体上各点的角速度相等,线速度υ=ωr,与半径r成正比;皮带传动(或齿轮传动)的两轮,在皮带不打滑的条件下,两轮边缘各点的线速度大小相等,角速度ω= ,与半径r成反比.
2.向心力
(1)来源:在匀速圆周运动中,向心力是物体受到的合力;在变速圆周运动中,向心力的大小等于物体受到的沿着半径方向的合力.F径台=F向=ma向.
(2)作用效果:向心力的方向始终指向圆心,与线速度方向垂直,因此它只改变线速度的方向,不改变线速度的大小.
友情提示 解决圆周运动的关键:正确受力分析,进行力的分解(沿法向和切向),建立F供=F需的关系.
3.离心运动
做匀速圆周运动的物体,在所受的合力突然消失时,物体将沿圆周的切线方向飞出做匀速直线运动;在所提供的合力大于所需要的向心力时,物体将做向心运动;在所提供的合力小于所需要的向心力时,物体将做离心运动.
4.竖直面内圆周运动的临界条件
(1)在图甲、乙所示的情景中:
( http: / / www.21cnjy.com )
①当υ= (即mg=m)时,
小球刚好能通过最高点,球和绳(或轨道)之间无相互作用.
②当υ> (即m>mg)时,图甲中绳对小球有向下的拉力,图乙中,轨道对小球有向下的支持力.
③当υ<时,小球不能通过最高点,即在到达最高点之前绳已松弛或球脱离轨道.
(2)在下图甲、乙所示的情景中:
甲 乙
①当υ=0时,轻杆(或内轨)对小球有竖直向上的支持力FN ,其大小等于小球的重力,即FN=mg.
②当0<υ<时,杆(或内轨)对小球的支持力的方向竖直向上,大小随速度的增大而减小,其取值范围是0
④当υ>时,杆(或外轨)对小球有指向圆心的力,其大小随速度的增大而增大,FN >0.
友情提示 (1)对“绳模型”而言,υ=是物体能否通过最高点的临界;对“杆模型”而言υ=是弹力竖直向上还是竖直向下的临界点.
(2)若物体还受到其他恒定的外力,可将该恒力与重力等效为新的“重力” mg' 进行分析,并确定相应的最高点.确定“等效重力”后,可用类比的方法确定其临界条件.
二、万有引力定律的应用
1.万有引力定律:F=G ,G=6.67×10-11 N·m2·kg-2,适用于两质点间的相互作用力.
2.万有引力定律的应用
(1)测天体的质量和密度
①利用天体表面的重力加速度g和天体的半径R.
在天体表面附近G =mg,故M = .
变换可得GM=gR2,称为“黄金代换”.
②利用天体的卫星:已知卫星的周期T(或线速度υ)和卫星的轨道半径r.
G = m = mr等,即可求M.
测天体密度:将M代入ρ= eq \f(M,πR3)即可确定天体的密度.
警示 (1)此方法只能确定中心天体的质量M.
(2)注意区分r的R的不同含义:r为轨道半径,R为天体半径,当卫星在天体表面运行时才有r =R.
(2)分析天体或卫星的运行规律
①把天体或卫星的运动近似看做圆周运动,它所需要的向心力由万有引力提供,即G = m=mrω2= mr=ma向.于是得到υ=eq \r(G),ω=eq \r(G),T=2πeq \r() , a向= G
由此可知:r增大,υ减小,ω减小,T增大,a向减小.
友情提示 (1)以上特点可概括为“越高越慢”.
(2)所有卫星的轨道平面都应过地心,即以地心为轨迹的圆心.
②地球同步卫星:相对于地面静止的人造卫星,它的周期T=24h.所以它只能位于赤道正上方某一确定高度h,h=()+-R≈3.6×104km,但它的质量可以不同.
3.三个宇宙速度
(1)第一宇宙速度υ1=7.9km/s是人造地球卫星的最小发射速度,最大绕行速度.
计算方法:①根据G =m,导出υ=eq \r().
②根据mg = m ,导出υ=.
(2)第二宇宙速度υ2=11.2km/s是物体挣脱地球的引力束缚需要的最小发射速度.
(3)第三宇宙速度υ3=16.7km/s是物体挣脱太阳的引力束缚需要的最小发射速度.
警示 虽然半径越大(离地面越高)的卫星环绕速度越小,但在发射过程中需要克服地球的引力做更多的功,增大势能,所以在地面上的发射速度也就越大,因此,不要认为υ环越小,υ发就越小.
DXLTPX典型例题剖析
一、描述圆周运动的各量之间的关系
【例1】 如图所示,一种向自行车灯供电的小发电机的上端有一半径r0=1.0cm的摩擦小轮,小轮与自行车车轮的边缘接触.当车轮转动时,因摩擦带动小轮转动,从而为发电机提供动力.自行车车轮的半径R1=35cm,小齿轮的半径R2=4.0cm,大齿轮的半径R3=10.0cm.求大齿轮的转速n3和摩擦小轮的转速n0之比.(假定摩擦小轮与自行车轮之间无相对滑动) ( )
( http: / / www.21cnjy.com )
【解析】 根据大、小齿轮两轮边缘各点的线速度大小相等,由υ=2πnR可得:2πn3R 3=2πn2R 2
因为小齿轮和车轮同轴转动,所以两轮上各点的转速相同,故有:n2= n1
小轮与自行车车轮的边缘接触,当车轮转动时,因摩擦而带动小轮转动,且两者无相对滑动,所以它们的线速度相同,则有:2πn1R 1=2πn0r0
由以上各式并代入数据可得大齿轮和摩擦小轮间的转速之比:,n3:n0=2:175.
【答案】 2:175
【总结评述】 凡是直接用皮带传动(包括链条传动、摩擦传动)的两个轮子,在不打滑时两轮边缘上各点的线速度大小相等;凡是同一个轮轴上(各个轮都绕同一根轴同步转动)的各点角速度相等(轴上的点除外).再根据描述圆周运动的各物理量之间的关系不难得出正确的结论.
变式训练 1
如图所示,半径为25crn的两圆柱体A和B,靠电动机带动按相同方向均以角速度ω=8rad/s转动.两圆柱体的转动轴互相平行且在同一水平面内,转动方向已在图中标出,质量分布均匀的木棒水平轻轻放置其上,重心在刚开始运动时恰在B的正上方,棒和圆柱间动摩擦因数为0.2,两圆柱中心间距离为l.5m,棒长大于3m,取g=10m/s2,求从棒开始运动到重心恰在A正上方需多长时间
【解析】两柱体线速度υ=ωR=2m/s
棒的加速度a=μg=2m/s2
加速时间t1= =1s
位移s1= t1 =1m
匀速时间t2= s=0.25s
共用时间t1+ t2=1.25s
【答案】 1.25s
二、圆周运动的向心力问题
【例2】(2009·华中师大附中)如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁.在不同的水平面上做匀速圆周运动,则以下叙述正确的是 ( )
( http: / / www.21cnjy.com )
A.物块A的线速度小于物块B的线速度
B.物块A的角速度大于物块B的角速度
C.物块A对漏斗内壁的压力大于物块B对漏斗内壁压力
D.物块A的周期大于物块B的周期
【解析】小物块A和B分别紧贴漏斗的内壁,分别到相同的重力和支持力,其合力F向=mgtanθ相同,由F向=m =mω2r=m() 2r且rB
变式训练 2
(2009山东临沂)如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽穿在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是 ( )
A.螺丝帽受的重力与最大静摩擦力平衡
B.螺丝帽受到杆的弹力方向水平向外,背离圆心
C.此时手转动塑料管的角速度ω=eq \r()
D.若杆的转动加快,螺丝帽有可能相对杆发生运动
【解析】 由于螺丝帽做圆周运动过程恰好不下滑,则竖直方向上重力与摩擦力平衡,杆对螺丝帽的弹力提供其做匀速圆周运动的向心力,选项A正确、BC错误;无论杆的转动速度增大多少,竖直方向受力平衡,故选项D错误.
【答案】 A
三、圆周运动中的临界问题
【例3】 如图所示,两绳系一个质量为m=0.1kg的小球,两绳的另一端分别固定于同一轴的A、B两处,上面绳长L=2m,两绳都拉直时与轴夹角分别为30°和45°,问球的角速度在什么范围内,两绳始终张紧 (g取10m/s2)
【解析】 两绳张紧时,小球受的力如图所示,当ω由0逐渐增大时,ω可能出现两个临界值.
( http: / / www.21cnjy.com )
(1)BC恰好拉直,但F2仍然为零,设此时的角速度ω1,则有
Fx=F1sin30°=mω12Lsin30°, ①
Fy=F1cos30°-mg=0, ②
联立①②代入数据得ω1=2.4rad/s
(2)AC由拉紧转为恰好拉直,但F1已为零,设此时的角速度为ω2,则有
Fx=F2sin45°=mω22Lsin30°, ③
Fy=F2cos45°-mg = 0, ④
联立③④代入已知数据得ω1=3.16rad/s
可见,要使两绳始终张紧,ω必须满足
2.40rad/s≤ω≤3.16rad/s.
【答案】 2.40rad/s≤ω≤3.16rad/s
【总结评述】 (1)要会用极限分析法判定物体可能处的状态,进而正确受力分析.
(2)要注意确定物体做圆周运动的圆心和半径.
(3)只要物体做圆周运动,在任何一个位置和状态,都满足F供=F需,建立该动力学关系是解决圆周运动问题的基本方法.
变式训练 3
(2008·江苏四市联考)如图所示,质量为m的小球置于正方体的光滑硬质盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为尺的匀速圆周运动,已知重力加速度为g,空气阻力不计,问:
( http: / / www.21cnjy.com )
(1)要使盒子在最高点时盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为多少
(2)若盒子以(1)中周期的做匀速圆周运动,则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大
【解析】 (1)设此时盒子的运动周期为T0,因为在最高点时盒子与小球之间刚好无作用力,因此小球仅受重力作用.根据牛顿运动定律得:mg=m,又υ=解得T0=2πeq \r()
(2)设此时盒子的运动周期为T,则此时小球的向心加速度为an=R由(1)知:g=R且T=
由上述三式知:an=4g
设小球受盒子右侧面的作用力为F,受上侧面的作用力为FN,根据牛顿运动定律知:
在水平方向上:F=man=4mg.
在竖直方向上:FN+mg=0,即FN =-mg
因为F为正值、FN为负值,所以小球对盒子的右侧面和下侧面有作用力,分别为4mg和rng.
【答案】 (1) =2πeq \r() (2)对右侧面压力为4mg,对下侧面压力为mg.
四、卫星或天体的运动
【例4】 (2009·四川)据报道,2009年4月29日,美国亚利桑那州一天文观测机构发现一颗与太阳系其它行星逆向运行的小行星,代号为2009HC82.该小行星绕太阳一周的时间为3.39年,直径2~3千米,其轨道平面与地球轨道平面呈l55°的倾斜.假定该小行星与地球均以太阳为中心做匀速圆周运动,则小行星和地球绕太阳运动的速度大小的比值为 ( )
A.3.39- B.3.39-
C.3.39 D.3.39
【解析】 本题考查天体运动问题,由万有引力提供向心力 =m行 =m地
由此可得:υ2行= υ2地= , =eq \r()
同理: = m行r行
= m地r地
将以上两式相比代入可知,A正确,B、C、D错,A正确。
【答案】 A
变式训练 4
(2009·江苏南京)2008年9月27日“神舟七号”宇航员翟志刚顺利完成出舱活动任务,他的第一次太空行走标志着中国航天事业全新时代的到来.“神舟七号”绕地球做近似匀速圆周运动,其轨道半径为r,若另有一颗卫星绕地球做匀速圆周运动的半径为2r,则可以确定 ( )
( http: / / www.21cnjy.com )
A.卫星与“神舟七号”的加速度大小之比为1:4
B.卫星与“神舟七号”的线速度大小之比为1:
C.翟志刚出舱后不再受地球引力
D.翟志刚出舱任务之一是取回外挂的实验样品,假如不小心实验样品脱手,则它做自由落地运动
【解析】 加速度计算公式为a= = ,所以卫星和“神舟七号”的加速度之比为l:4,A选项正确;线速度计算公式为υ=eq \r(),所以卫星和“神舟七号”的线速度之比为l:,B选项正确;翟志刚出舱后依然受到地球的引力,引力提供其做匀速圆周运动所需的向心力,C选项错误;实验样品脱手后,依然做匀速圆周运动,相对飞船静止,D选项错误。
【答案】 AB
五、卫星(或飞行器)的变轨问题
【例5】 (2009·山东)2008年9月25日至28日,我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是 ( )
A.飞船变轨前后的机械能相等
B.飞船在圆轨道上时航天员出舱前后都处于失重状态
C.飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度
D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度
【解析】 本题主要考查向心力及功能关系,飞船变轨时加速外力做功,机械能不守恒,A错,飞船在轨道上运行时万有引力提供向心力处于失重状态,启正确,飞船在此轨道上运行时期为90分钟,小于同步卫星周期,由T= 可知C正确, =ma,可知二者加速度相等,D错,正确答案BC.
【答案】 BC
友情提示 在变轨中不能再利用G =m,生来推导结论,因万有引力恰好等于向心力时,飞船是在圆轨道上行的,而非进行变轨.变轨时应从两方面考虑:一是地球拱的引力F引= ,在开始变轨时F引不变;二是飞船需要的向心力F向=m,可以通过改变飞船的速度来变它所需要的向心力,从而达到使其做向心运动或离心功而变轨的目的.
变式训练 5
(2008·南通调研)如图所示,“嫦娥一号”探月卫星入月球轨道后,首先在椭圆轨道I上运动,P、Q两点是轨道I的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道I和Ⅱ在P点相切,关于探月卫星的运动,下列说正确的是 ( )
( http: / / www.21cnjy.com )
A.卫星在轨道I上运动周期大于在Ⅱ上运动的周期
B.卫星由轨道I进入轨道Ⅱ必须要在P点减速
C.卫星在轨道I上运动时,P点的速度小于Q点的速度
D.卫星在轨道I上运动时,P点的加速度小于Q点的加速度
【解析】 由开普勒第三定律可知,椭圆轨道上,围绕同一中心天体运行的天体,半长轴越长,周期越长,A正确;在P点由轨道l进入轨道Ⅱ时,由于要做近心运动,月球提供的引力不变的情况下,必须使其减速,所需要的向心力变小,才能达到目的,B正确;在同一椭圆轨道上,近月点处速度大于远月点处速度,C错误;近月点万有引力大于在远月点万有引力,向心加速度在近月点处大,D错误.
【答案】 AB
温馨提示:
同学们:针对你们所学内容的巩固与掌握,请认真完成课后强化作业(五)及阶段性测试题(二)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 6 页) 版权所有@21世纪教育网
同课章节目录
