人教A版2003课标高中数学必修1第三章 3.1.2用二分法求方程的近似解
文档属性
| 名称 | 人教A版2003课标高中数学必修1第三章 3.1.2用二分法求方程的近似解 |  | |
| 格式 | zip | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-13 21:34:15 | ||
图片预览








文档简介
课件20张PPT。3.1.2 用二分法求方程的近似解合肥十中 数学组 1)对于函数y=f(x),我们把使f(x)=0的 实数x 叫函数y=f(x)的零点复习2)方程 f(x)=0有实数根 问题提出2.对于高次多项式方程,在十六世纪已找到了三次和四次方程的求根公式,但对于高于4次的方程,类似的努力却一直没有成功. 到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于4次的代数方程不存在求根公式,即不存在用四则运算及根号表示的一般的公式解.同时,即使对于3次和4次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法. 用二分法求方程的近似解思考1:从百草园到三味书屋的电缆有5个接点.现
在某处发生故障,需及时修理.为了尽快把故障
缩小在两个接点之间,一般至少需要检查多少___次.21 2 3 4 5知识探究(一):二分法的概念 你能继续缩小零点所在的区间吗?思考2:
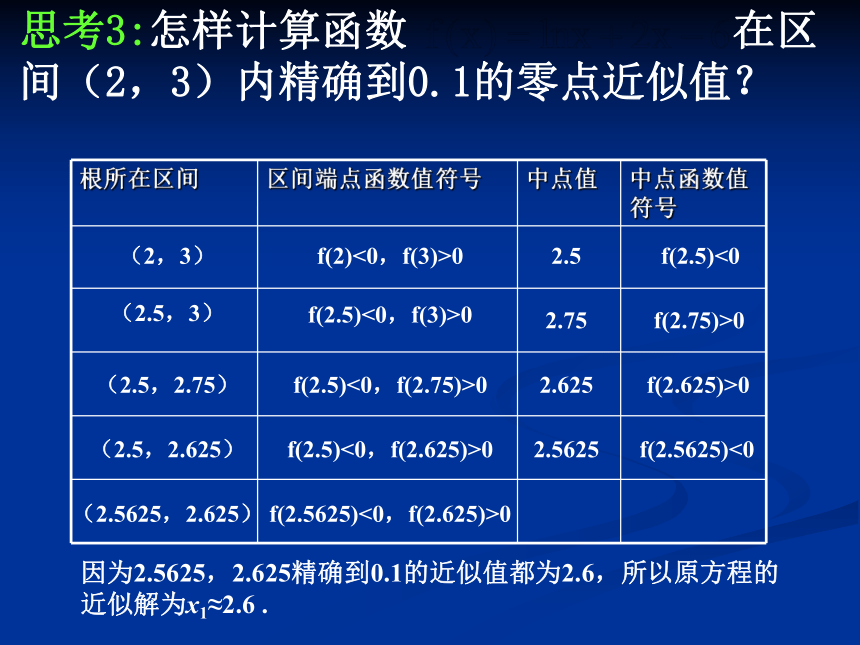
假设上例的故障点大概是函数f(x)=lnx+2x-6的零点位置,请同学们猜想它的零点所在大致区间。因为2.5625,2.625精确到0.1的近似值都为2.6,所以原方程的
近似解为x1≈2.6 .(2,3)f(2)<0,f(3)>02.5f(2.5)<0(2.5,3)f(2.5)<0,f(3)>02.75f(2.75)>0(2.5,2.75)f(2.5)<0,f(2.75)>02.625f(2.625)>0(2.5,2.625)f(2.5)<0,f(2.625)>02.5625f(2.5625)<0(2.5625,2.625)f(2.5625)<0,f(2.625)>0思考4:上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么? . 对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数
y=f(x),通过不断地把函数f(x)的零点所在的区间
一分为二,使区间的两个端点逐步逼近零点,进
而得到零点近似值的方法叫做二分法(bisection).思考:下列函数中能用二分法求零点的是____. (1) (4)知识探究(二):
用二分法求函数零点近似值的步骤 思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|m—n|<ε时,区间[m,n]内的任意一个值都是函数零点的近似值.往往取端点值作为零点的近似值。 用二分法求函数零点近似值的基本步骤:3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b). 2. 求区间(a,b)的中点c;1.确定区间[a,b],使f(a)·f(b)<0 ,给定精度ε;理论迁移解:令f(x)= 2x+3x-7,则把问题转化为求
函数的零点,用二分法
智力游戏12只球中有一只假球,假球比真球略轻.现有一座无砝码的天平,如何用最少的次数称出这只假球? 课堂小结1.二分法定义
二分法是求函数零点近似解的一种计算方法.
2.解题步骤
①确定初始区间
②计算并确定下一区间,定端点值符号
③循环进行,达到精确度。
3.二分法渗透了逼近的数学思想.作业
《赢在课堂》相关习题
《同步作业》相关习题 谢谢!
在某处发生故障,需及时修理.为了尽快把故障
缩小在两个接点之间,一般至少需要检查多少___次.21 2 3 4 5知识探究(一):二分法的概念 你能继续缩小零点所在的区间吗?思考2:
假设上例的故障点大概是函数f(x)=lnx+2x-6的零点位置,请同学们猜想它的零点所在大致区间。因为2.5625,2.625精确到0.1的近似值都为2.6,所以原方程的
近似解为x1≈2.6 .(2,3)f(2)<0,f(3)>02.5f(2.5)<0(2.5,3)f(2.5)<0,f(3)>02.75f(2.75)>0(2.5,2.75)f(2.5)<0,f(2.75)>02.625f(2.625)>0(2.5,2.625)f(2.5)<0,f(2.625)>02.5625f(2.5625)<0(2.5625,2.625)f(2.5625)<0,f(2.625)>0思考4:上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么? . 对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数
y=f(x),通过不断地把函数f(x)的零点所在的区间
一分为二,使区间的两个端点逐步逼近零点,进
而得到零点近似值的方法叫做二分法(bisection).思考:下列函数中能用二分法求零点的是____. (1) (4)知识探究(二):
用二分法求函数零点近似值的步骤 思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|m—n|<ε时,区间[m,n]内的任意一个值都是函数零点的近似值.往往取端点值作为零点的近似值。 用二分法求函数零点近似值的基本步骤:3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b). 2. 求区间(a,b)的中点c;1.确定区间[a,b],使f(a)·f(b)<0 ,给定精度ε;理论迁移解:令f(x)= 2x+3x-7,则把问题转化为求
函数的零点,用二分法
智力游戏12只球中有一只假球,假球比真球略轻.现有一座无砝码的天平,如何用最少的次数称出这只假球? 课堂小结1.二分法定义
二分法是求函数零点近似解的一种计算方法.
2.解题步骤
①确定初始区间
②计算并确定下一区间,定端点值符号
③循环进行,达到精确度。
3.二分法渗透了逼近的数学思想.作业
《赢在课堂》相关习题
《同步作业》相关习题 谢谢!
