24.1.4圆周角同步练习含答案
图片预览

文档简介
新人教版九年级上册24.1.4 圆周角同步练习
一.选择题(共5小题)
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A.30° B.60° C.30°或150° D.60°或120°
3.如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A.3﹣ B. C.3﹣ D.3﹣
4.如图,△ABC中,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )
A.5 B.6 C.7 D.8
5.下列命题:①圆周角等于圆心角的一半;②x=2是方程x﹣1=1的解;③平行四边形既是中心对称图形又是轴对称图形;④的算术平方根是4.其中真命题的个数有( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
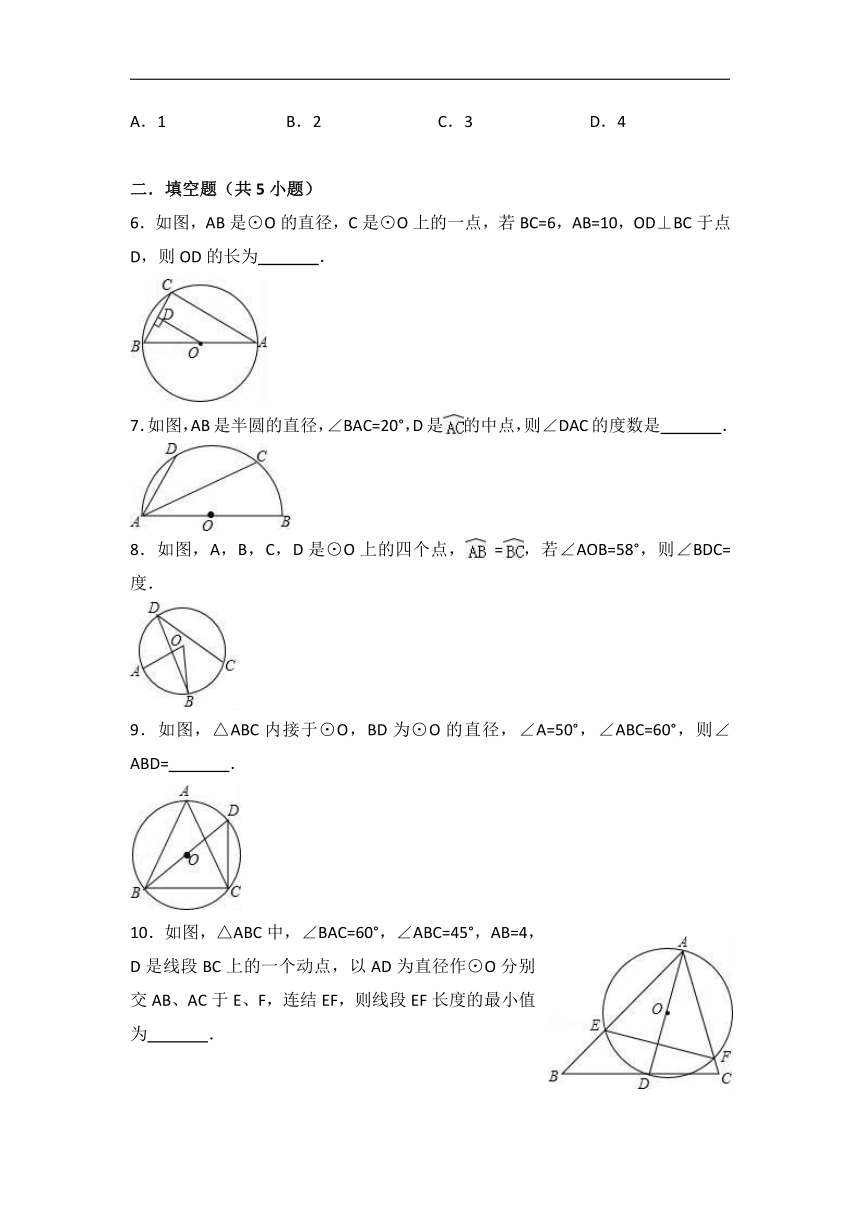
6.如图,AB是⊙O的直径,C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
7.如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是 .
8.如图,A,B,C,D是⊙O上的四个点, =,若∠AOB=58°,则∠BDC= 度.
9.如图,△ABC内接于⊙O,BD为⊙O的直径,∠A=50°,∠ABC=60°,则∠ABD= .
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为 .
三.解答题(共4小题)
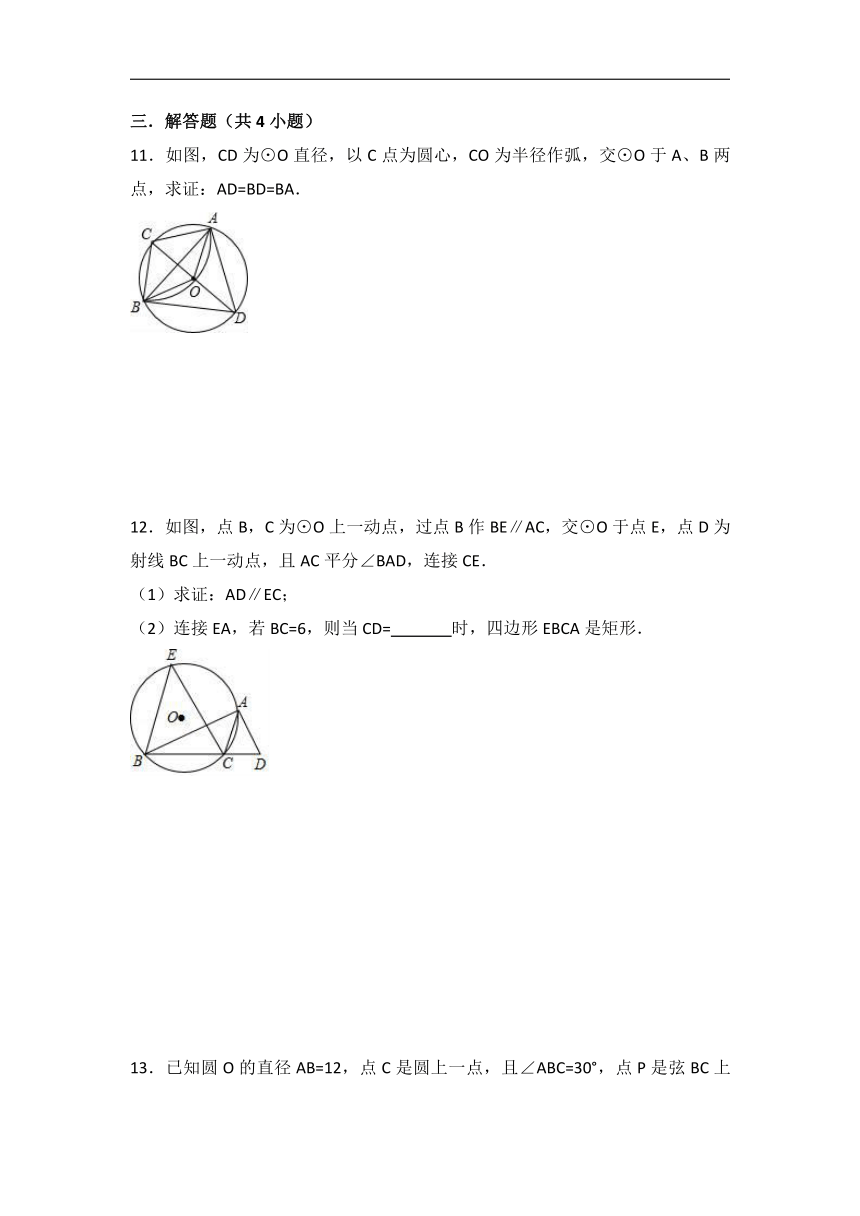
11.如图,CD为⊙O直径,以C点为圆心,CO为半径作弧,交⊙O于A、B两点,求证:AD=BD=BA.
12.如图,点B,C为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.
(1)求证:AD∥EC;
(2)连接EA,若BC=6,则当CD= 时,四边形EBCA是矩形.
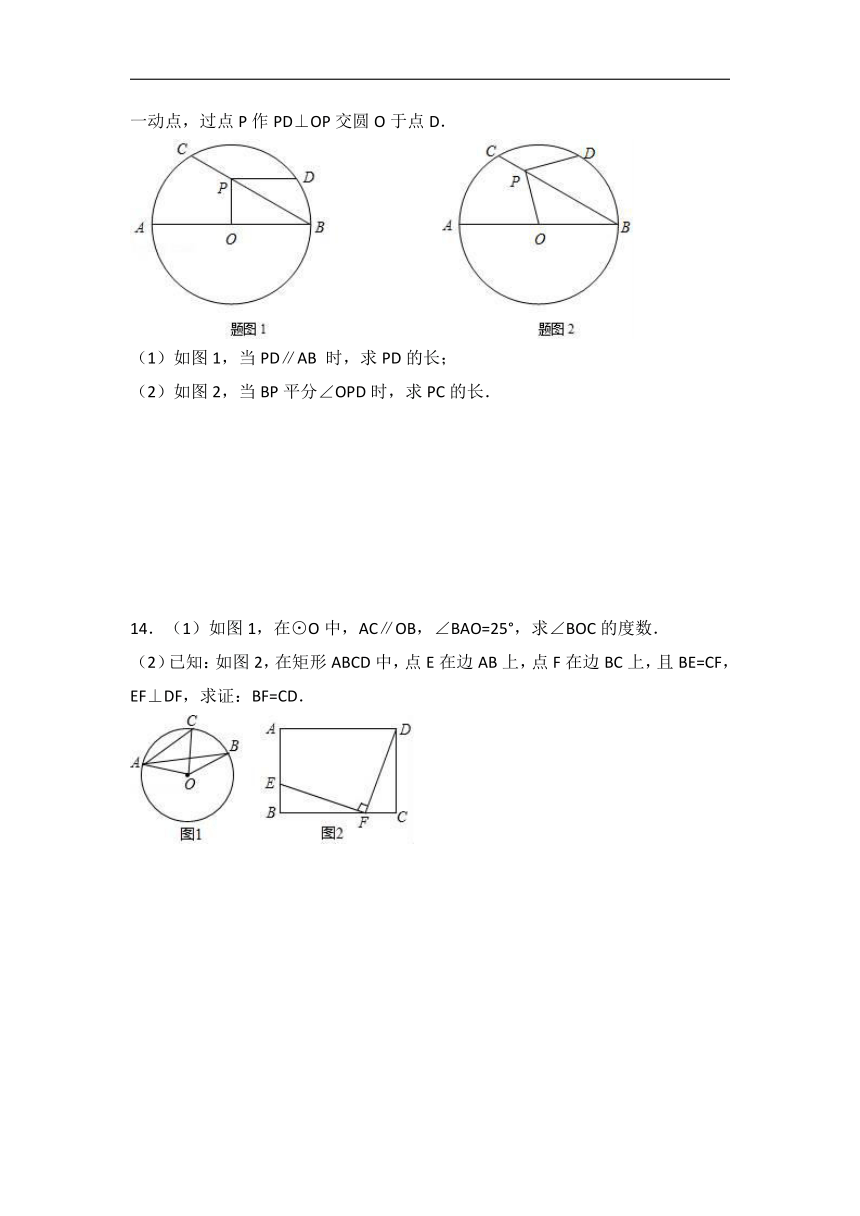
13.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.
(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
14.(1)如图1,在⊙O中,AC∥OB,∠BAO=25°,求∠BOC的度数.
(2)已知:如图2,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
参考答案
一.选择题(共5小题)
1.D.
2.D.
3.D.
4.D.
5.A.
二.填空题
6.4.
7.35°.
8.29.
9.20°.
10..
三.解答题
11.证明:∵CA=CB=CO,
∴OB=BC=OC=OA=AC,
∴△OBC和△OAC都是等边三角形,
∴∠BCO=∠ACO=60°,∠BOC=∠AOC=60°,
∴∠AOB=120°,
∴∠ADB=60°,
∴∠ACD=∠BCD=∠ADB,
∴==,
∴AD=BD=BA.
12.(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠E=∠BAC,
∴∠E=∠DACM
∵BE∥AC,
∴∠E=∠ACE,
∴∠ACE=∠DAC,
∴AD∥EC.
(2)解:当四边形ACBE是矩形时,∠ACB=90°,
∴∠ACB=∠ACD=90°,
∵∠BAC=∠DAC,
∴∠ABD=∠D,
∴AB=AD,
∴BC=CD=6,
故答案为6.
13.解:如图1,联结OD
∵直径AB=12
∴OB=OD=6
∵PD⊥OP
∴∠DPO=90°
∵PD∥AB
∴∠DPO+∠POB=180°
∴∠POB=90°
又∵∠ABC=30°,OB=6
∴
∵在Rt△POD 中,PO2+PD2=OD2
∴
∴
(2)如图2,过点O 作OH⊥BC,垂足为H
∵OH⊥BC
∴∠OHB=∠OHP=90°
∵∠ABC=30°,OB=6
∴,
∵在⊙O 中,OH⊥BC
∴
∵BP 平分∠OPD
∴
∴PH=OH?cot45°=3
∴.
14.
解:(1)∵OA=OB,∠BAO=25°,
∴∠B=25°.
∵AC∥OB,
∴∠B=∠CAB=25°,
∴∠BOC=2∠CAB=50°;
(2)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠CFD=90°,
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD,
在△BEF和△CFD中,
,
∴△BEF≌△CFD(ASA),
∴BF=CD.
一.选择题(共5小题)
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A.30° B.60° C.30°或150° D.60°或120°
3.如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A.3﹣ B. C.3﹣ D.3﹣
4.如图,△ABC中,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )
A.5 B.6 C.7 D.8
5.下列命题:①圆周角等于圆心角的一半;②x=2是方程x﹣1=1的解;③平行四边形既是中心对称图形又是轴对称图形;④的算术平方根是4.其中真命题的个数有( )
A.1 B.2 C.3 D.4
二.填空题(共5小题)
6.如图,AB是⊙O的直径,C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
7.如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是 .
8.如图,A,B,C,D是⊙O上的四个点, =,若∠AOB=58°,则∠BDC= 度.
9.如图,△ABC内接于⊙O,BD为⊙O的直径,∠A=50°,∠ABC=60°,则∠ABD= .
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为 .
三.解答题(共4小题)
11.如图,CD为⊙O直径,以C点为圆心,CO为半径作弧,交⊙O于A、B两点,求证:AD=BD=BA.
12.如图,点B,C为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.
(1)求证:AD∥EC;
(2)连接EA,若BC=6,则当CD= 时,四边形EBCA是矩形.
13.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.
(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
14.(1)如图1,在⊙O中,AC∥OB,∠BAO=25°,求∠BOC的度数.
(2)已知:如图2,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
参考答案
一.选择题(共5小题)
1.D.
2.D.
3.D.
4.D.
5.A.
二.填空题
6.4.
7.35°.
8.29.
9.20°.
10..
三.解答题
11.证明:∵CA=CB=CO,
∴OB=BC=OC=OA=AC,
∴△OBC和△OAC都是等边三角形,
∴∠BCO=∠ACO=60°,∠BOC=∠AOC=60°,
∴∠AOB=120°,
∴∠ADB=60°,
∴∠ACD=∠BCD=∠ADB,
∴==,
∴AD=BD=BA.
12.(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠E=∠BAC,
∴∠E=∠DACM
∵BE∥AC,
∴∠E=∠ACE,
∴∠ACE=∠DAC,
∴AD∥EC.
(2)解:当四边形ACBE是矩形时,∠ACB=90°,
∴∠ACB=∠ACD=90°,
∵∠BAC=∠DAC,
∴∠ABD=∠D,
∴AB=AD,
∴BC=CD=6,
故答案为6.
13.解:如图1,联结OD
∵直径AB=12
∴OB=OD=6
∵PD⊥OP
∴∠DPO=90°
∵PD∥AB
∴∠DPO+∠POB=180°
∴∠POB=90°
又∵∠ABC=30°,OB=6
∴
∵在Rt△POD 中,PO2+PD2=OD2
∴
∴
(2)如图2,过点O 作OH⊥BC,垂足为H
∵OH⊥BC
∴∠OHB=∠OHP=90°
∵∠ABC=30°,OB=6
∴,
∵在⊙O 中,OH⊥BC
∴
∵BP 平分∠OPD
∴
∴PH=OH?cot45°=3
∴.
14.
解:(1)∵OA=OB,∠BAO=25°,
∴∠B=25°.
∵AC∥OB,
∴∠B=∠CAB=25°,
∴∠BOC=2∠CAB=50°;
(2)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠CFD=90°,
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD,
在△BEF和△CFD中,
,
∴△BEF≌△CFD(ASA),
∴BF=CD.
同课章节目录
