人教版九年级上册24.3正多边形和圆课堂测试卷含答案
文档属性
| 名称 | 人教版九年级上册24.3正多边形和圆课堂测试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-13 00:00:00 | ||
图片预览

文档简介
2018年 九年级数学上册 圆 正多边形与圆 课堂测试卷
一、选择题:
1、下列说法中,正确的是( )
A.三角形的内心到三角形的三个顶点的距离相等
B.三点确定一个圆
C.垂直于半径的直线一定是这个圆的切线
D.任何三角形有且只有一个内切圆
2、如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2)? C.(1,3) D.(3,1)
3、如图,已知⊙O的内接四边形ABCD,AD=,CD=1,半径为1,则∠B的度数为( )
A.60° B.70° C.75° D.80°
4、正六边形的边心距与边长之比为( )
A.1:2 B.:2? C.:1?? D.:2
5、如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
A.30°? ? B.15°?? ? C.60°? ? D.45°
6、如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108°? B.144°? C.150°? D.166°
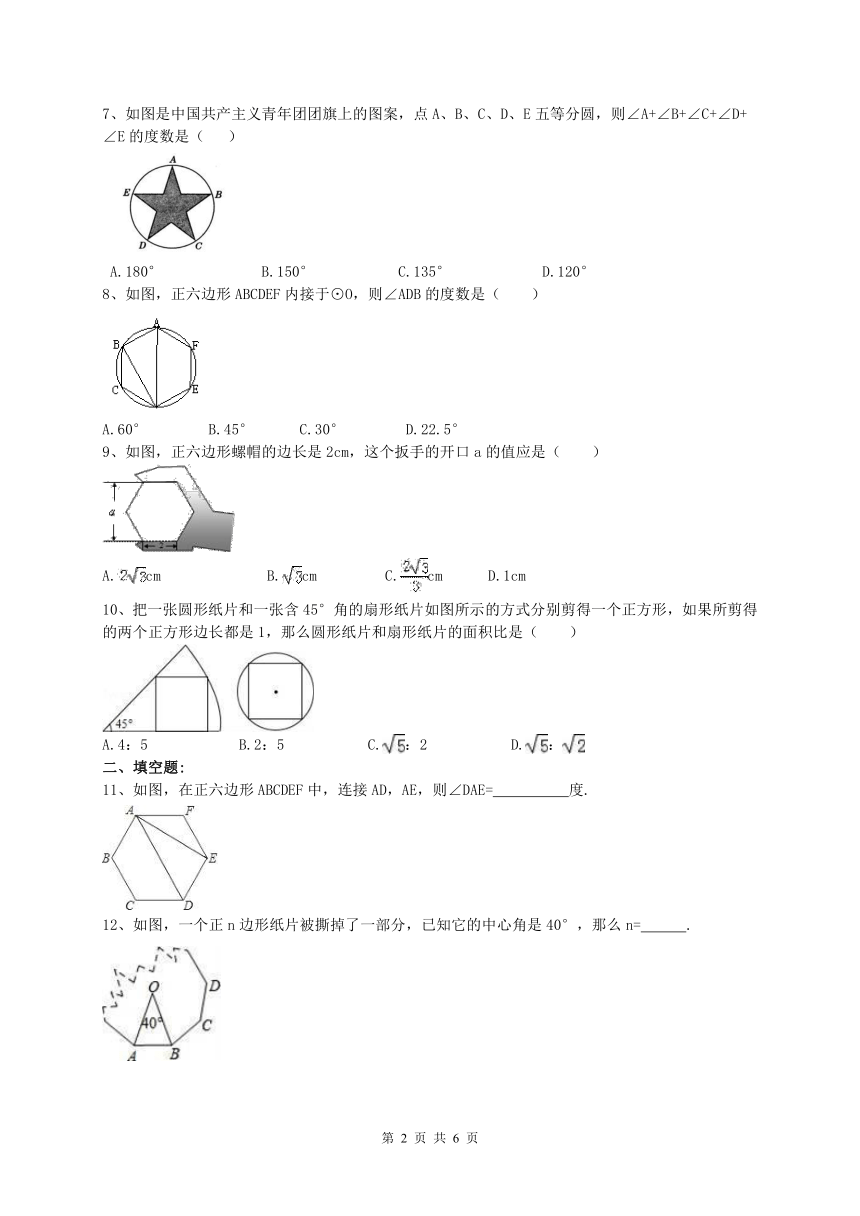
7、如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是(? )
?
A.180°?? ? B.150°? ? C.135°? D.120°
8、如图,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( )
A.60° B.45° C.30° D.22.5°
9、如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A.cm? B.cm?? C.cm? D.1cm
10、把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C.:2?? D.:
二、填空题:
11、如图,在正六边形ABCDEF中,连接AD,AE,则∠DAE=?????度.
12、如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n= .
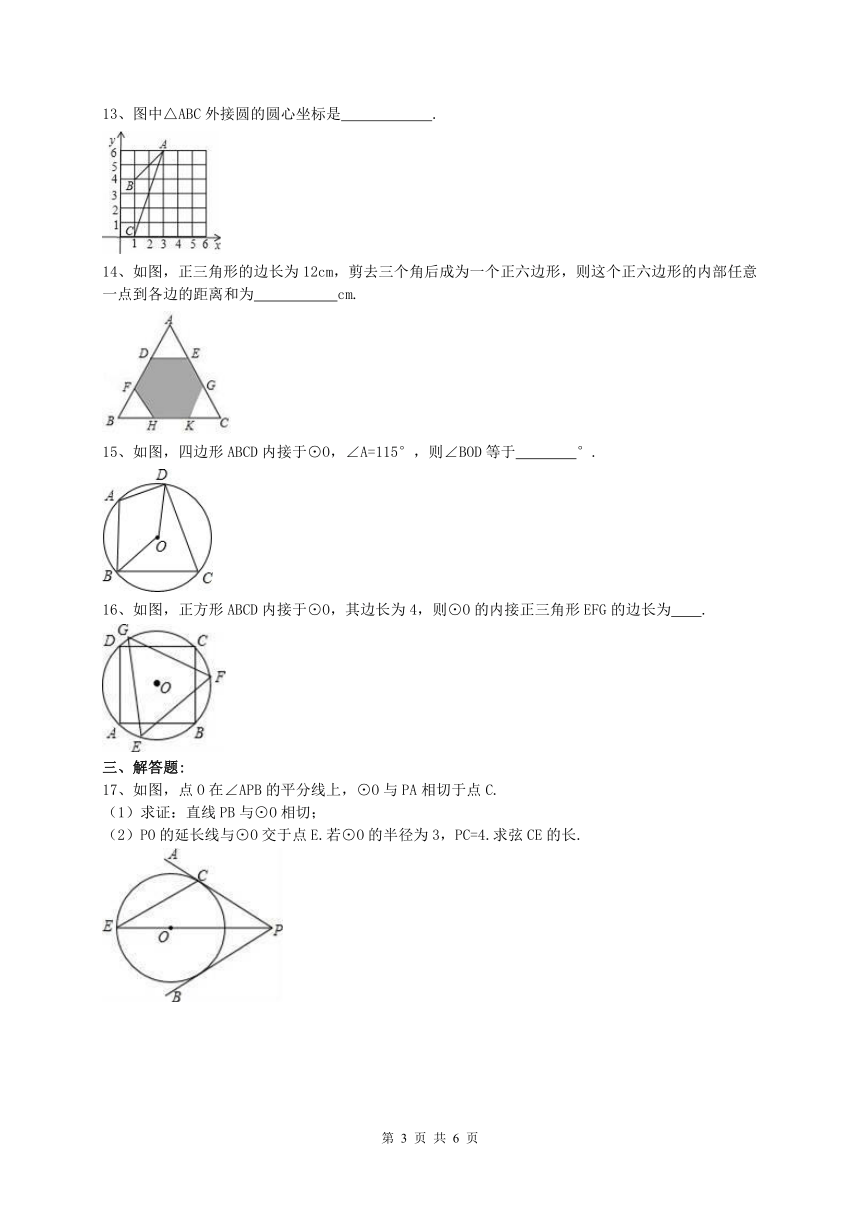
13、图中△ABC外接圆的圆心坐标是 .
14、如图,正三角形的边长为12cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为 ??? cm.
15、如图,四边形ABCD内接于⊙O,∠A=115°,则∠BOD等于 °.
16、如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
三、解答题:
17、如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
18、如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线.
(2)若CB=2,CE=4,求⊙O的半径r及AE的长.
19、如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
20、如图1、2、3、…、n,M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案
1、D.
2、D.
3、C.
4、D.
5、D.
6、B.
7、A
8、C
9、A.
10、A.
11、答案为:300? ??
12、答案为:9.
13、答案为:(5,2).
14、答案为:????
15、答案为:130.
16、答案为2.
17、(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C,∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,∴OD=OC.
∴直线PB与⊙O相切;
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.∵⊙O与PA相切于点C,∴∠PCF=∠E.
又∵∠CPF=∠EPC,∴△PCF∽△PEC,∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径,∴∠ECF=90°.设CF=x,则EC=2x.则x2+(2x)2=62,
解得x=.则EC=2x=.
18、(1)证明:连接OE;∵AD是∠BAF的平分线,∴∠CAE=∠DAE.
∵OA=OE,∴∠CAE=∠OEA.∴∠OEA=∠DAE.∴OE∥AD,
∵ED⊥AF,∴∠OEC=∠ADC=90°.∴OE⊥DC.∴CD是⊙O的切线.
(2)解:连接BE,∵CB=2,CE=4,根据切割线定理:CE2=CB?AC,∴AC=8,∴AB=8﹣2=6,
∵AB为⊙O的直径,∴⊙O的半径r为3,∵CD是⊙O的切线,∴∠CEB=∠CAE,
∵∠BCE=∠ACE,∴△CBE∽△CEA,∴==,∴BE=AE,
∵AB为⊙O的直径,∴∠AEB=90°,∴AE2+BE2=AB2,即AE2+AE2=62,∴AE=.
19、(1)证明:连接OC.如图1所示∵AC平分∠DAB,∴∠DAC=∠OAC,
∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OCA,∴DA∥OC,
∵AD⊥DC,∴∠ADC=90°,∴∠OCD=90°,即OC⊥DC,∵OC为半径,∴DC为⊙O的切线.
(2)解:连接BC,如图2所示:∵AB是⊙O的直径,∴AB=10,∠ACB=90°=∠ADC,
∴AC=8,又∵∠DAC=∠OAC,∴△ACD∽△ABC,∴,即,解得:CD=4.8.
20、解:分别连接OB、OC,
(1)∵AB=AC,∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,∴CO平分∠ACB∴∠OBC=∠OCB=30°,∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,∴△OMB≌△ONC,∴∠BOM=∠NOC,
∵∠BAC=60°,∴∠BOC=120°;∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON==120°;在(2)中,∠MON==90°;
在(3)中∠MON==72°…,故当n时,∠MON=.
一、选择题:
1、下列说法中,正确的是( )
A.三角形的内心到三角形的三个顶点的距离相等
B.三点确定一个圆
C.垂直于半径的直线一定是这个圆的切线
D.任何三角形有且只有一个内切圆
2、如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2)? C.(1,3) D.(3,1)
3、如图,已知⊙O的内接四边形ABCD,AD=,CD=1,半径为1,则∠B的度数为( )
A.60° B.70° C.75° D.80°
4、正六边形的边心距与边长之比为( )
A.1:2 B.:2? C.:1?? D.:2
5、如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
A.30°? ? B.15°?? ? C.60°? ? D.45°
6、如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108°? B.144°? C.150°? D.166°
7、如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是(? )
?
A.180°?? ? B.150°? ? C.135°? D.120°
8、如图,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( )
A.60° B.45° C.30° D.22.5°
9、如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A.cm? B.cm?? C.cm? D.1cm
10、把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C.:2?? D.:
二、填空题:
11、如图,在正六边形ABCDEF中,连接AD,AE,则∠DAE=?????度.
12、如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n= .
13、图中△ABC外接圆的圆心坐标是 .
14、如图,正三角形的边长为12cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为 ??? cm.
15、如图,四边形ABCD内接于⊙O,∠A=115°,则∠BOD等于 °.
16、如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
三、解答题:
17、如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
18、如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线.
(2)若CB=2,CE=4,求⊙O的半径r及AE的长.
19、如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
20、如图1、2、3、…、n,M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案
1、D.
2、D.
3、C.
4、D.
5、D.
6、B.
7、A
8、C
9、A.
10、A.
11、答案为:300? ??
12、答案为:9.
13、答案为:(5,2).
14、答案为:????
15、答案为:130.
16、答案为2.
17、(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C,∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,∴OD=OC.
∴直线PB与⊙O相切;
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.∵⊙O与PA相切于点C,∴∠PCF=∠E.
又∵∠CPF=∠EPC,∴△PCF∽△PEC,∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径,∴∠ECF=90°.设CF=x,则EC=2x.则x2+(2x)2=62,
解得x=.则EC=2x=.
18、(1)证明:连接OE;∵AD是∠BAF的平分线,∴∠CAE=∠DAE.
∵OA=OE,∴∠CAE=∠OEA.∴∠OEA=∠DAE.∴OE∥AD,
∵ED⊥AF,∴∠OEC=∠ADC=90°.∴OE⊥DC.∴CD是⊙O的切线.
(2)解:连接BE,∵CB=2,CE=4,根据切割线定理:CE2=CB?AC,∴AC=8,∴AB=8﹣2=6,
∵AB为⊙O的直径,∴⊙O的半径r为3,∵CD是⊙O的切线,∴∠CEB=∠CAE,
∵∠BCE=∠ACE,∴△CBE∽△CEA,∴==,∴BE=AE,
∵AB为⊙O的直径,∴∠AEB=90°,∴AE2+BE2=AB2,即AE2+AE2=62,∴AE=.
19、(1)证明:连接OC.如图1所示∵AC平分∠DAB,∴∠DAC=∠OAC,
∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OCA,∴DA∥OC,
∵AD⊥DC,∴∠ADC=90°,∴∠OCD=90°,即OC⊥DC,∵OC为半径,∴DC为⊙O的切线.
(2)解:连接BC,如图2所示:∵AB是⊙O的直径,∴AB=10,∠ACB=90°=∠ADC,
∴AC=8,又∵∠DAC=∠OAC,∴△ACD∽△ABC,∴,即,解得:CD=4.8.
20、解:分别连接OB、OC,
(1)∵AB=AC,∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,∴CO平分∠ACB∴∠OBC=∠OCB=30°,∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,∴△OMB≌△ONC,∴∠BOM=∠NOC,
∵∠BAC=60°,∴∠BOC=120°;∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON==120°;在(2)中,∠MON==90°;
在(3)中∠MON==72°…,故当n时,∠MON=.
同课章节目录
