空间几何体的三视图和直观图习题1.2
文档属性
| 名称 | 空间几何体的三视图和直观图习题1.2 |

|
|
| 格式 | zip | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-15 21:54:02 | ||
图片预览




文档简介
课件23张PPT。空间几何体的三视图和直观图
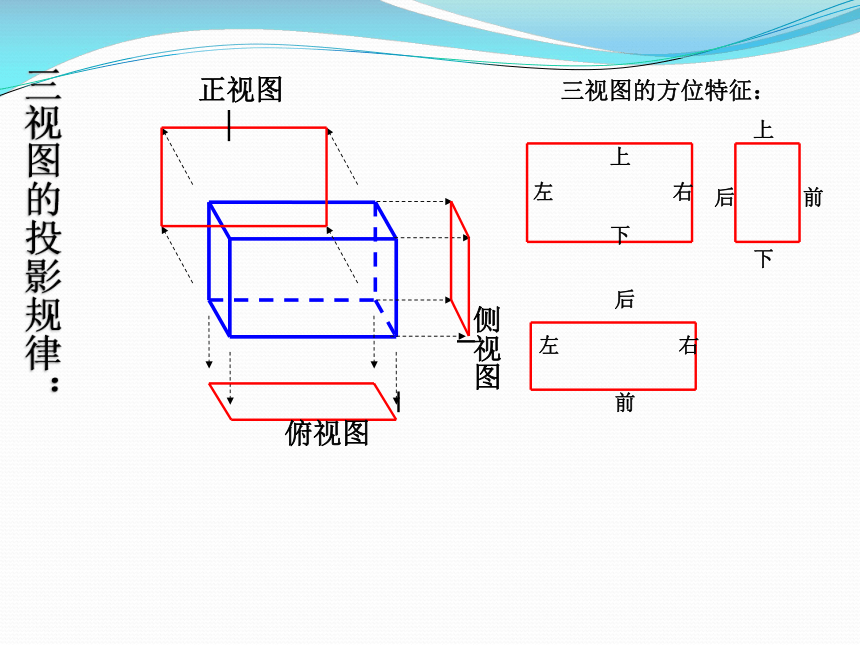
习题1.2三视图的投影规律: 左 右左 右后 前上 下上
下后
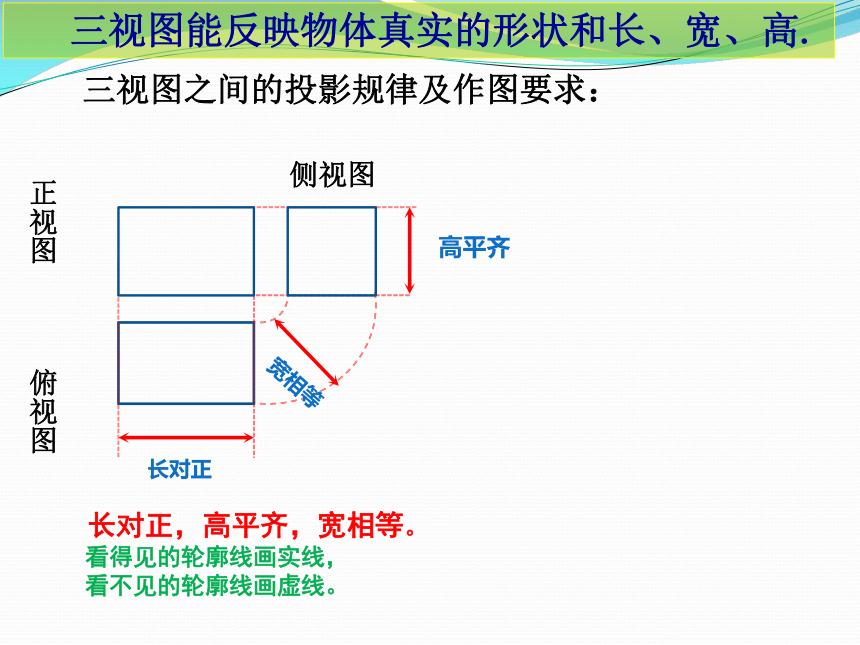
前三视图的方位特征:正视图 俯视图 三视图之间的投影规律及作图要求: 三视图能反映物体真实的形状和长、宽、高. 高平齐宽相等长对正侧视图 长对正,高平齐,宽相等。
看得见的轮廓线画实线,
看不见的轮廓线画虚线。
课前练习:
1.一个几何体的正视图为一个三角形,则这个几 何体可能是下列几何体中的 .(填入所有可能的几何体前的编号)
①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱
⑤圆锥 ⑥圆柱
`1、2、3、52.如果一个几何体的三视图中含有一个圆,则这个
几何体不可能是( )
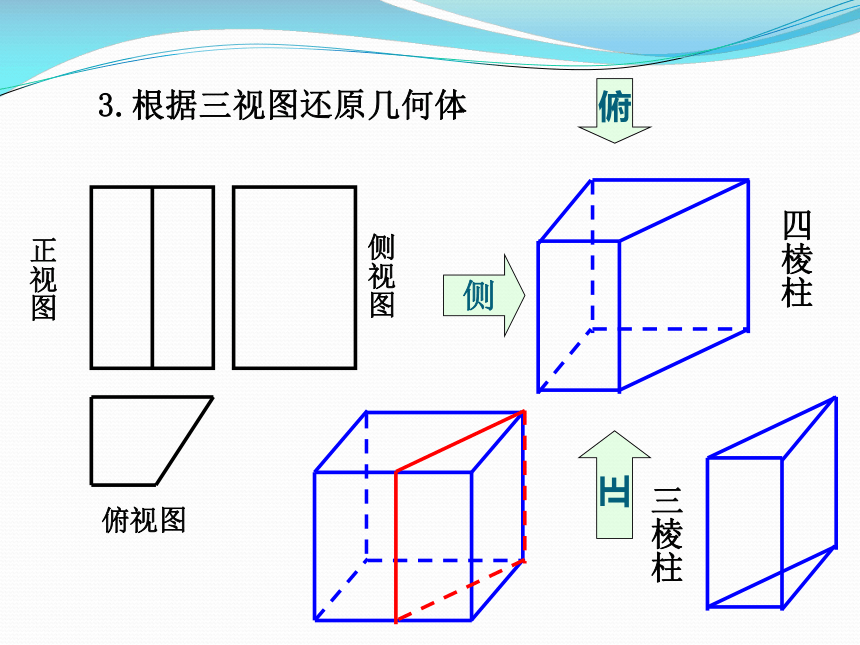
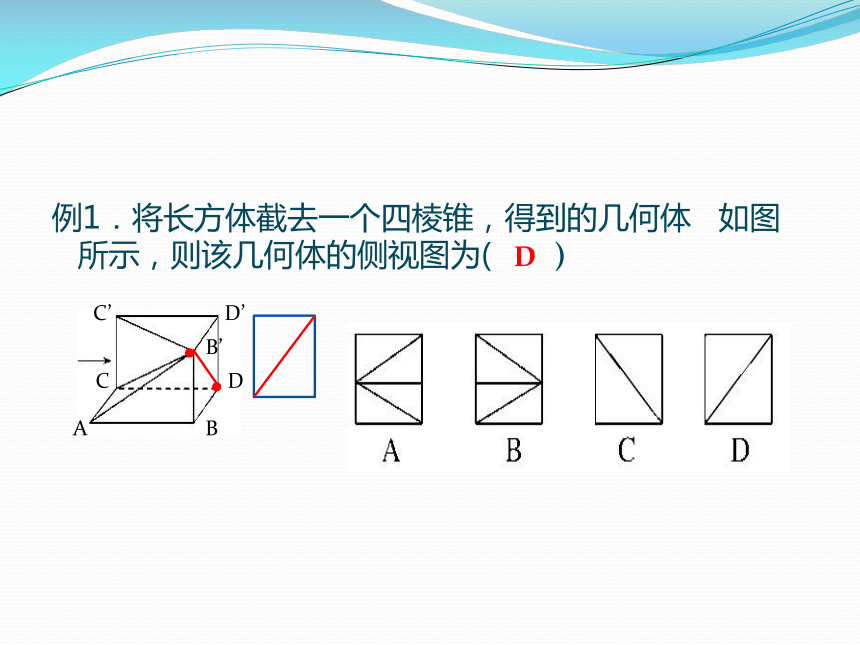
A球 B圆柱 C圆台 D棱台D3.根据三视图还原几何体正视图侧视图俯视图 1.绘制几何体的三视图例1.将长方体截去一个四棱锥,得到的几何体 如图所示,则该几何体的侧视图为( )
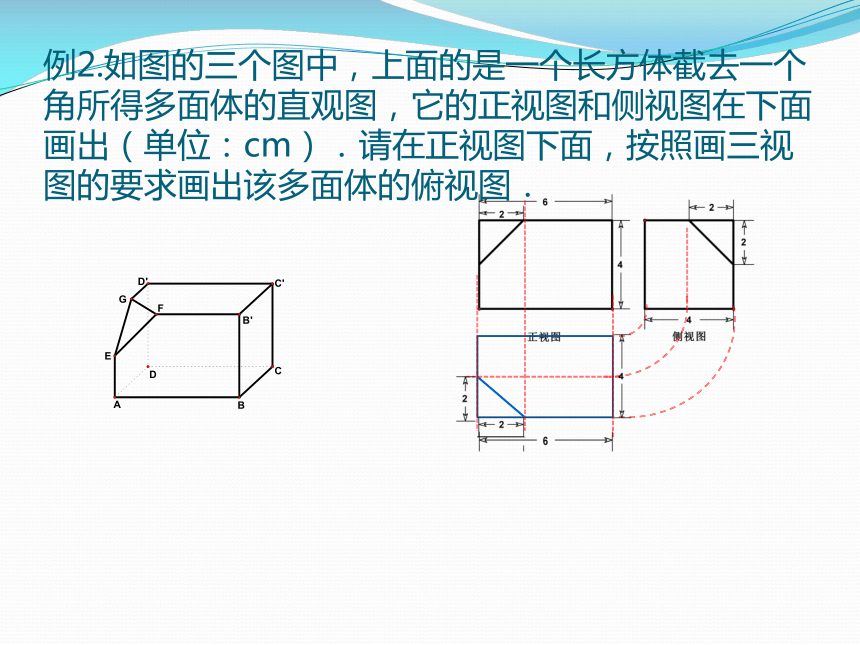
DA B B’C DC’ D’例2.如图的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图. ? 总结:绘制多面体三视图时,先作出几何体顶点的投影,然后确定棱的投影,从而确定面和体的投影。2.三视图还原直观图探究2:能否由三视图直接判断几何体类别? 基本几何体的直观图与三视图三视图中如果含有圆或者圆弧,则与旋转体有关,
含多边形则不能确定!例1.在一个几何体的三视图中,
正视图和俯视图如图所示,
则相应的侧视图可以为( )
D例2.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为 练习:某棱锥的三视图如图所示,该棱锥最长棱的棱长为( ) 例3.三棱锥的三视图如图所示,画出该三棱锥直观图A’三视图还原方法总结:1.记忆基本几何体常规放置下的三视图模型
2.借用长方体切割法
3.借用长方体定点,去点还原法
4.最后要检验直观图和三视图是否吻合三视图与直观图习题课小结:1.绘制三视图规范要求和步骤;
2.利用基本几何体三视图特征还原简单直观图
3.借助长方体还原三视图的原理和方法。
课后作业.
1.如图所示,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC且
3AA′=BB′=CC′=AB,则
多面体ABC-A′B′C′的正视图是( ) 练2.某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为__________。3.某棱锥的三视图如图所示,该棱锥最长棱的棱长为( )4、某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A.8 B.6
C.10 D.85(思考题*).如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的n条棱中,最长的棱的长度
习题1.2三视图的投影规律: 左 右左 右后 前上 下上
下后
前三视图的方位特征:正视图 俯视图 三视图之间的投影规律及作图要求: 三视图能反映物体真实的形状和长、宽、高. 高平齐宽相等长对正侧视图 长对正,高平齐,宽相等。
看得见的轮廓线画实线,
看不见的轮廓线画虚线。
课前练习:
1.一个几何体的正视图为一个三角形,则这个几 何体可能是下列几何体中的 .(填入所有可能的几何体前的编号)
①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱
⑤圆锥 ⑥圆柱
`1、2、3、52.如果一个几何体的三视图中含有一个圆,则这个
几何体不可能是( )
A球 B圆柱 C圆台 D棱台D3.根据三视图还原几何体正视图侧视图俯视图 1.绘制几何体的三视图例1.将长方体截去一个四棱锥,得到的几何体 如图所示,则该几何体的侧视图为( )
DA B B’C DC’ D’例2.如图的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图. ? 总结:绘制多面体三视图时,先作出几何体顶点的投影,然后确定棱的投影,从而确定面和体的投影。2.三视图还原直观图探究2:能否由三视图直接判断几何体类别? 基本几何体的直观图与三视图三视图中如果含有圆或者圆弧,则与旋转体有关,
含多边形则不能确定!例1.在一个几何体的三视图中,
正视图和俯视图如图所示,
则相应的侧视图可以为( )
D例2.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为 练习:某棱锥的三视图如图所示,该棱锥最长棱的棱长为( ) 例3.三棱锥的三视图如图所示,画出该三棱锥直观图A’三视图还原方法总结:1.记忆基本几何体常规放置下的三视图模型
2.借用长方体切割法
3.借用长方体定点,去点还原法
4.最后要检验直观图和三视图是否吻合三视图与直观图习题课小结:1.绘制三视图规范要求和步骤;
2.利用基本几何体三视图特征还原简单直观图
3.借助长方体还原三视图的原理和方法。
课后作业.
1.如图所示,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC且
3AA′=BB′=CC′=AB,则
多面体ABC-A′B′C′的正视图是( ) 练2.某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为__________。3.某棱锥的三视图如图所示,该棱锥最长棱的棱长为( )4、某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A.8 B.6
C.10 D.85(思考题*).如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的n条棱中,最长的棱的长度
