空间中的平行关系复习（一）

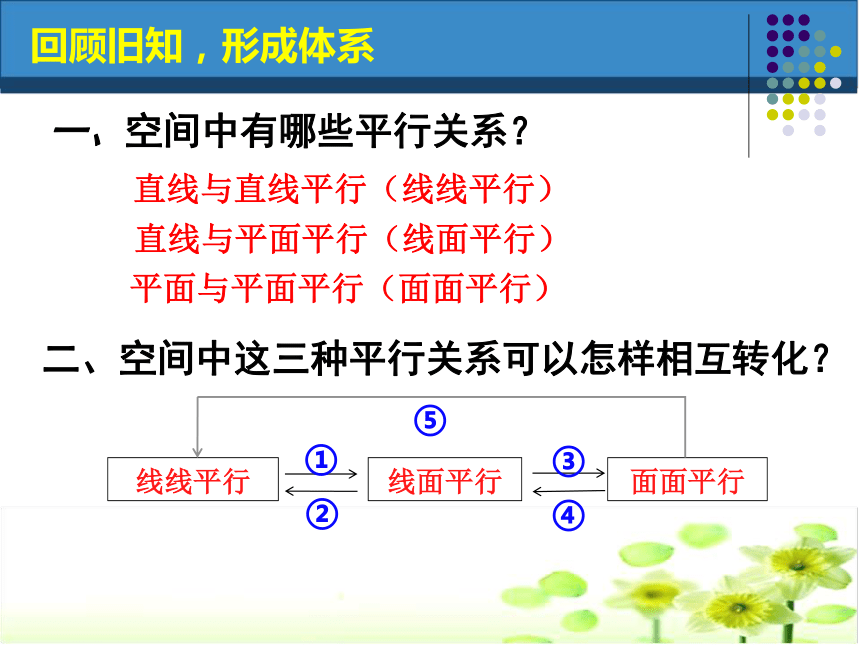
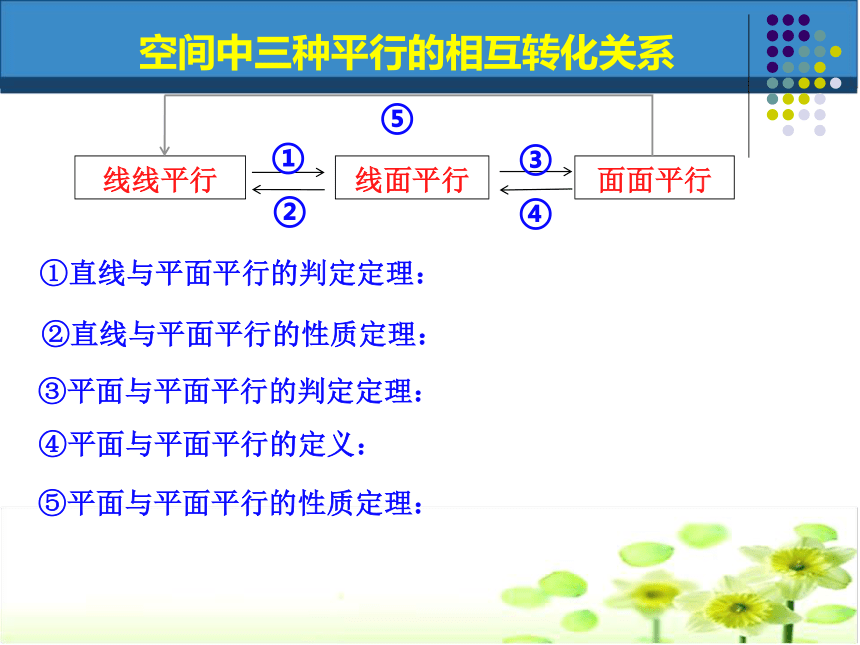
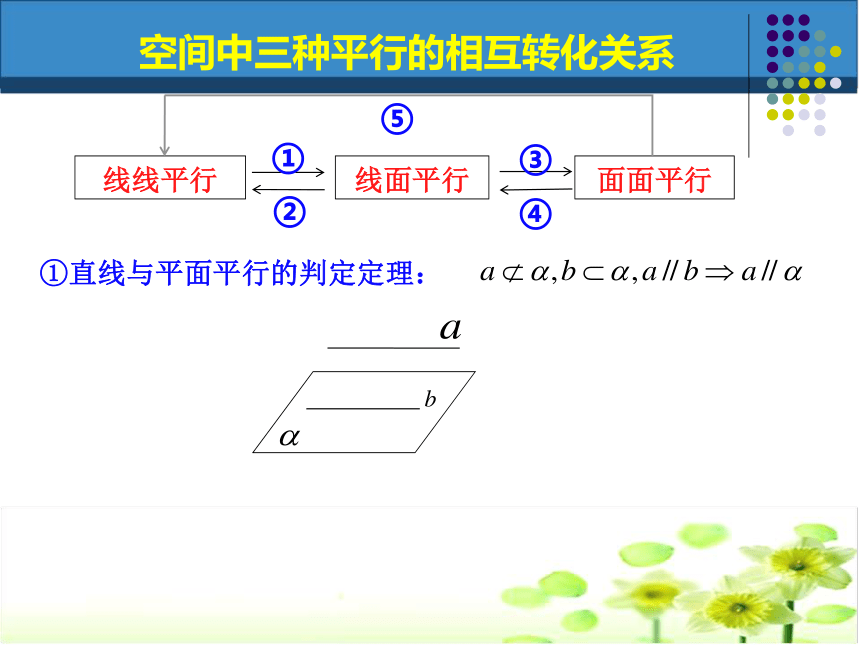
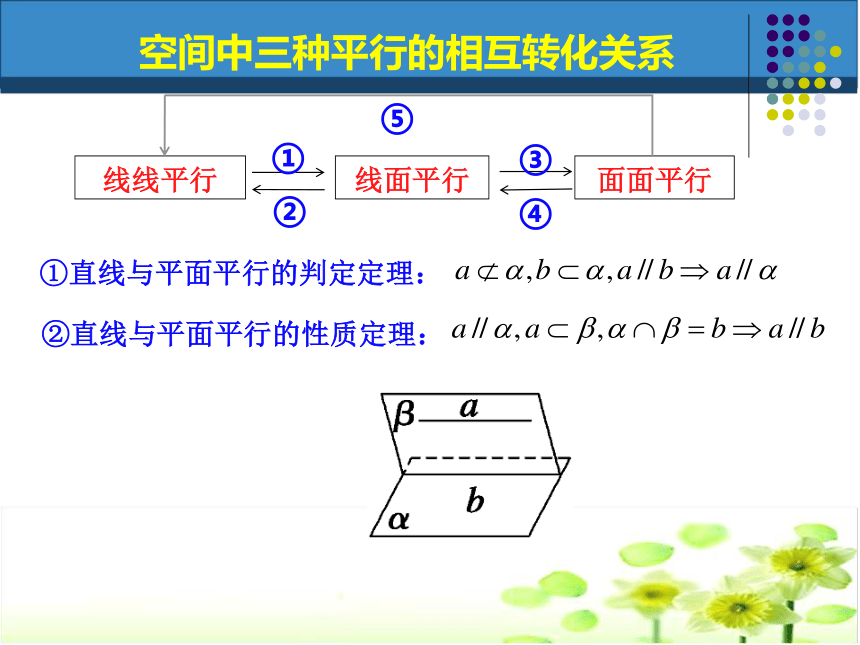
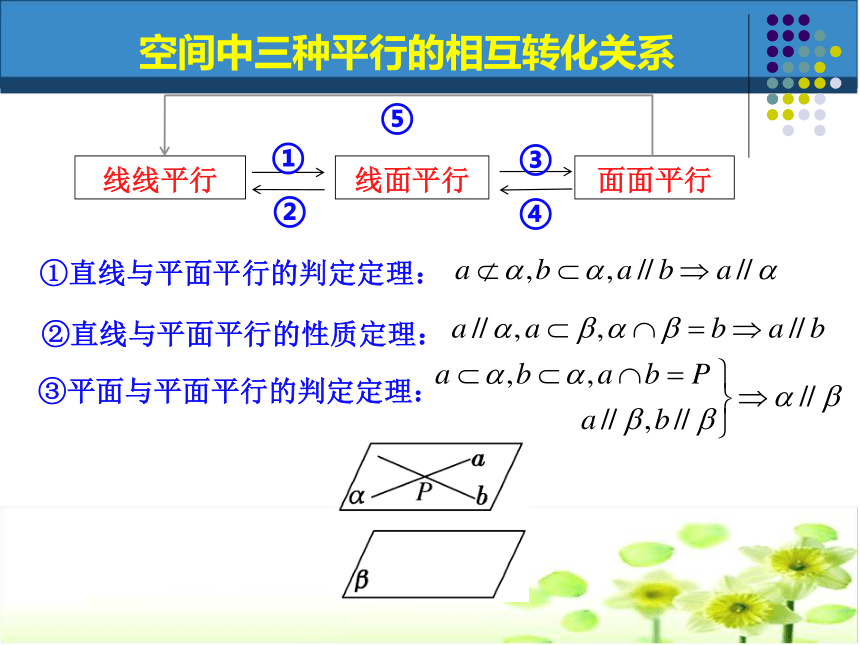
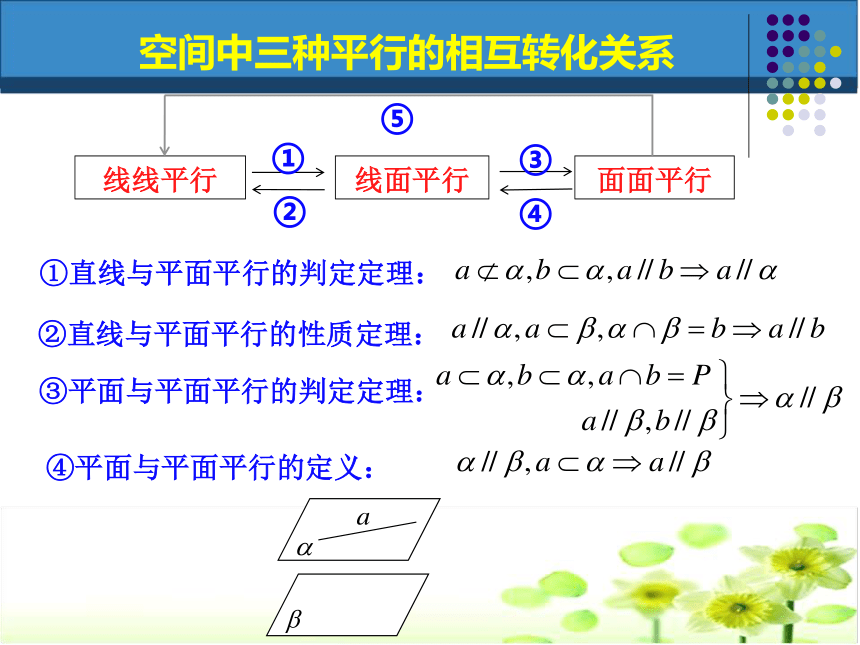
课件19张PPT。空间中的平行关系（一）直线与直线平行（线线平行）直线与平面平行（线面平行）平面与平面平行（面面平行） 回顾旧知，形成体系一、空间中有哪些平行关系？二、空间中这三种平行关系可以怎样相互转化？①直线与平面平行的判定定理：②直线与平面平行的性质定理：③平面与平面平行的判定定理：⑤平面与平面平行的性质定理：④平面与平面平行的定义：空间中三种平行的相互转化关系①直线与平面平行的判定定理：空间中三种平行的相互转化关系①直线与平面平行的判定定理：②直线与平面平行的性质定理：空间中三种平行的相互转化关系①直线与平面平行的判定定理：②直线与平面平行的性质定理：③平面与平面平行的判定定理：空间中三种平行的相互转化关系①直线与平面平行的判定定理：②直线与平面平行的性质定理：③平面与平面平行的判定定理：空间中三种平行的相互转化关系④平面与平面平行的定义：①直线与平面平行的判定定理：②直线与平面平行的性质定理：③平面与平面平行的判定定理：⑤平面与平面平行的性质定理：④平面与平面平行的定义：空间中三种平行的相互转化关系①直线与平面平行的判定定理：②直线与平面平行的性质定理：③平面与平面平行的判定定理：空间中三种平行的相互转化关系④平面与平面平行的定义：⑤平面与平面平行的性质定理：?o平行小题体验，夯实基础小题体验，夯实基础BD例1.如图,四棱锥P—ABCD中,底面ABCD为平行四边形，F为AB的中点，E为PD的中点. (1)求证:PB//平面AEC.突出重点，促进思维(2)在PC上求一点G，使FG∥平
面AEC，并证明你的结论．变式：小结：1.由“中点”想“中点”。2.证线线平行常用方法：中位线，平行四边形，平行公理，线面平行，面面平行。突破难点，提升思维变式：过A,M,N三点的平面与直线PB
相交于点Q，E为BC的中点
求证：平面MNC//平面AEQ.突破难点，提升思维1.空间中三种平行的相互转化关系归纳小结，巩固提升归纳小结，巩固提升2.证明线线平行的常用方法：（1）中位线（2）平行四边形（3）平行公理
（4）线面平行（5）面面平行（1）线线平行 （2）面面平行3.证明线面平行的常用方法：4.证明面面平行的常用方法：线面平行 5.两种能力，一种思想：（1）空间想象能力和逻辑推理能力 （2）转化思想 1．如图，直三棱柱ABC-A1B1C1 中，AB=2AA1 ， ，M是AB的中点，△A1MC1是等腰三角形，D为CC1的中点，E为BC上一点．
（Ⅰ）若DE∥平面A1MC1，求 ；
（Ⅱ）平面A1MC1将三棱柱ABC-A1B1C1分成两个部分，求较小部分与较大部分的体积之比．，2.如图，在四棱锥P-ABCD中，侧棱PA底面ABCD，底面ABCD为矩形，AD=2AB=2PA=2，E为PA上一点，且PE=2ED.
（1）若F为PE的中点，求证：BF//平面AEC；
（2）求三棱锥P-AEC的体积.练习巩固，反馈创新感谢指导！突破难点，提升思维