3.1直线的倾斜角与斜率 课件
文档属性
| 名称 | 3.1直线的倾斜角与斜率 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 301.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-15 22:01:21 | ||
图片预览







文档简介
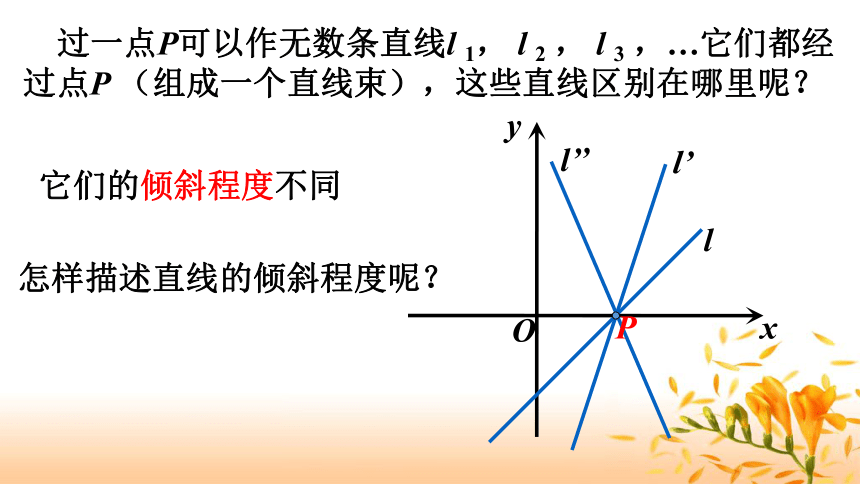
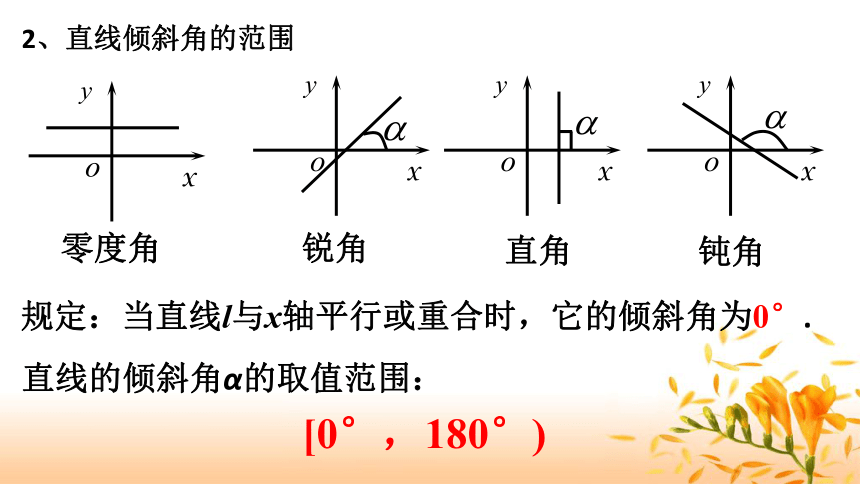
课件22张PPT。创设情境 两点确定一条直线.一点能确定一条直线的位置吗?已知直线 l 经过点P,直线 l 的位置能够确定吗?答:不能 过一点P可以作无数条直线l 1, l 2 , l 3 ,…它们都经过点P (组成一个直线束),这些直线区别在哪里呢?它们的倾斜程度不同怎样描述直线的倾斜程度呢?3.1.1 倾斜角与斜率第三章 直线与方程3.1 直线的倾斜角与斜率确立目标1、理解直线的倾斜角与斜率的概念;2、掌握求直线斜率的两种方法;3、了解在平面直角坐标系中确定一条直线的几何要素.重点:1、直线的倾斜角和斜率的概念;2、过两点的直线的斜率公式.难点:1、倾斜角和斜率的对应关系;2、求直线的倾斜角和斜率.目标:展开自学1、直线倾斜角的概念;2、直线倾斜角的范围;3、确定平面直角坐标系中一条直线位置的几何要素是什么?4、直线的斜率的概念;5、探究:由两点确定的直线的斜率怎么求?自学课本82页~85页内容,完成下列问题:反馈矫正1、直线倾斜角的概念 当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.下列四图中,表示直线的倾斜角的是( )A 2、直线倾斜角的范围零度角 锐角 直角 钝角 规定:当直线l与x轴平行或重合时,它的倾斜角为0°.直线的倾斜角α的取值范围:[0°,180°)想一想你认为下列说法对吗?1、任意一条直线都有唯一确定的倾斜角与它对应.2、每一个倾斜角都对应于唯一的一条直线.对错3、确定平面直角坐标系中一条直线位置的几何要素是什么?确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角, 二者缺一不可. 已知直线上的一个点不能确定一条直线的位置;同样已知直线的倾斜角α.也不能确定一条直线的位置.但是,直线上的一个点和这条直线的倾斜角可以唯一确定一条直线.4、直线的斜率的概念;日常生活中,有没有表示倾斜程度的量呢?是否可以用直线倾斜角的正切来描述直线的倾斜程度呢? 一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即倾斜角是90°的直线没有斜率.当0°<α<90°时,即α为锐角时,当90°<α<180°时,即α为钝角时,k>0k<0如图,当α为锐角,且 P1P2方向向上时, (1)锐角 5、探究:由两点确定的直线的斜率怎么求?如图,当α为钝角,且P1P2方向向上时, (2)钝角 当P2P1的方向向上时1、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?答:适用,因为分子为0,分母不为0,所以k=0. 对公式的理解2、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?答:不适用, 因为分母为0,无意义.例题 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.A(3,2)C(0,-1)B(-4,1)解:讨论总结1、直线的倾斜角定义及其范围:2、直线的斜率定义:当堂训练 ①因为所有直线都有倾斜角,所以所有直线都有斜率.( ) ②因为平行于y轴的直线的斜率不存在,所以平行于y轴的直线的
倾斜角不存在.( )③直线的倾斜角越大,则直线的斜率越大.( ) 1、判断正误:2、课本86页练习1、解:2、解:谢谢指导!再见!
倾斜角不存在.( )③直线的倾斜角越大,则直线的斜率越大.( ) 1、判断正误:2、课本86页练习1、解:2、解:谢谢指导!再见!
