4.3.2 空间两点间的距离公式
图片预览






文档简介
课件19张PPT。 4.3.2 空间两点间的距离公式
教学目标:1.掌握空间两点间的距离公式,会用空间两点间的距离公式解决问题
2.会利用中点坐标公式求出空间线段的中点坐标。
3.掌握空间点关于坐标轴和坐标面的对称。思考如何计算空间两点之间的距离?思考思
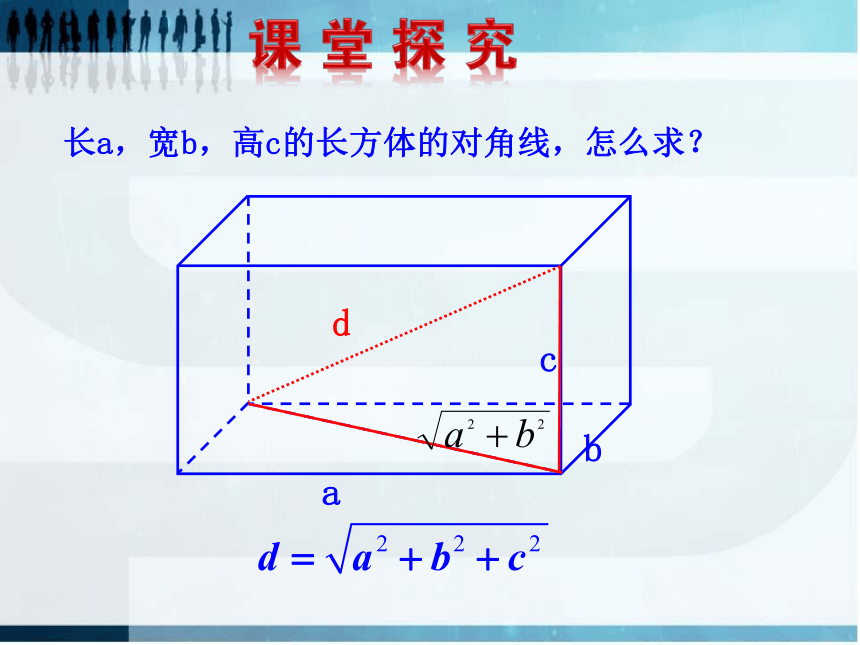
考长a,宽b,高c的长方体的对角线,怎么求?2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?如图:P1、P2是空间中任意两点,且坐标为P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).在xOy平面上,过点P1作P2N的垂线,垂足为H,则所以因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)之间的距离 在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z),类比平面两点的中点坐标可以得二、空间中点坐标公式小组讨论点M(x,y,z)是空间直角坐标系O-xyz中的一点(1)与点M关于x轴对称的点:(2)与点M关于y轴对称的点:(3)与点M关于z轴对称的点:合作探究一点M(x,y,z)是空间直角坐标系O-xyz中的一点(1)与点M关于x轴对称的点:(2)与点M关于y轴对称的点:(3)与点M关于z轴对称的点:(x,-y,-z)(-x,y,-z)(-x,-y,z)规律:关于谁对称谁不变,其余的相反。点M(x,y,z)是空间直角坐标系O-xyz中的一点(5)与点M关于平面xOy的对称点:(6)与点M关于平面yOz的对称点:(7)与点M关于平面xOz的对称点:合作探究二点M(x,y,z)是空间直角坐标系O-xyz中的一点(5)与点M关于平面xOy的对称点:(x,y,-z)(-x,y,z)(x,-y,z)规律:关于谁对称谁不变,其余的相反。(6)与点M关于平面yOz的对称点:(7)与点M关于平面xOz的对称点:类比猜想一、两点间距离公式
教学目标:1.掌握空间两点间的距离公式,会用空间两点间的距离公式解决问题
2.会利用中点坐标公式求出空间线段的中点坐标。
3.掌握空间点关于坐标轴和坐标面的对称。思考如何计算空间两点之间的距离?思考思
考长a,宽b,高c的长方体的对角线,怎么求?2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?如图:P1、P2是空间中任意两点,且坐标为P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).在xOy平面上,过点P1作P2N的垂线,垂足为H,则所以因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)之间的距离 在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z),类比平面两点的中点坐标可以得二、空间中点坐标公式小组讨论点M(x,y,z)是空间直角坐标系O-xyz中的一点(1)与点M关于x轴对称的点:(2)与点M关于y轴对称的点:(3)与点M关于z轴对称的点:合作探究一点M(x,y,z)是空间直角坐标系O-xyz中的一点(1)与点M关于x轴对称的点:(2)与点M关于y轴对称的点:(3)与点M关于z轴对称的点:(x,-y,-z)(-x,y,-z)(-x,-y,z)规律:关于谁对称谁不变,其余的相反。点M(x,y,z)是空间直角坐标系O-xyz中的一点(5)与点M关于平面xOy的对称点:(6)与点M关于平面yOz的对称点:(7)与点M关于平面xOz的对称点:合作探究二点M(x,y,z)是空间直角坐标系O-xyz中的一点(5)与点M关于平面xOy的对称点:(x,y,-z)(-x,y,z)(x,-y,z)规律:关于谁对称谁不变,其余的相反。(6)与点M关于平面yOz的对称点:(7)与点M关于平面xOz的对称点:类比猜想一、两点间距离公式
