圆的方程习题4-1课件
图片预览






文档简介
课件16张PPT。人教A版数学必修二第四章 圆与方程复习、提升课圆的标准方程圆的一般方程一 复习回顾问题:那么圆的标准方程与一般方程有什么联系呢?问题:那么圆的标准方程与一般方程有什么联系呢?一 复习回顾二 基础练习?(1,0)??三 能力提升例1:(习题4.1A组3)已知圆C的圆心在直线x-2y-1=0上,并且经过原点和A(2,1),求圆C的标准方程. 解法一:设所求圆的标准方程为
由条件知
解得
故所求圆的标准方程为
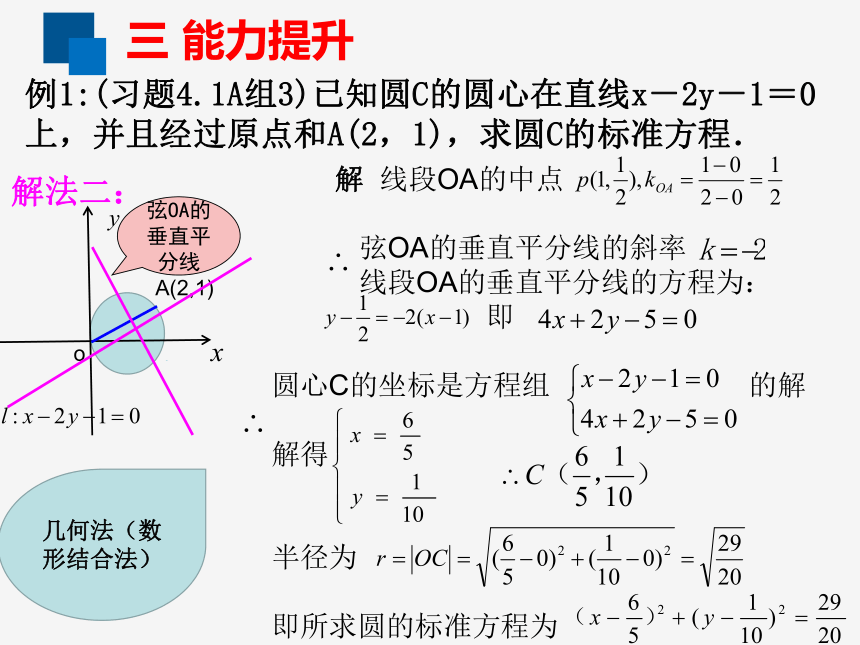
待定系数法 解法二:
解 线段OA的中点
弦OA的垂直平分线的斜率
线段OA的垂直平分线的方程为:
即
圆心C的坐标是方程组 的解
解得
半径为
即所求圆的标准方程为
弦OA的垂直平分线几何法(数形结合法)例1:(习题4.1A组3)已知圆C的圆心在直线x-2y-1=0上,并且经过原点和A(2,1),求圆C的标准方程.三 能力提升解法三:
∵ 圆心C在直线 上,
∴可设点C的坐标为
又∵该圆经过A,O两点,∴
∴
解得 ∴圆心坐标为
半径为
即所求圆的标准方程为
例1:(习题4.1A组3)已知圆C的圆心在直线x-2y-1=0上,并且经过原点和A(2,1),求圆C的标准方程.三 能力提升
求圆的标准方程的方法:
(1)待定系数法:
①设圆的标准方程为(x-a)2+(y-b)2=r2(r>0);
②由条件列方程(组)解得a,b,r的值;
③写出圆的标准方程
(2)直接法
①一般先从确定圆的两个要素入手,即先求出圆心的坐标和半径,再写出圆的标准方程.
②确定圆心和半径时,常用到中点坐标公式、两点间的距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点为圆心”等.
例题小结:(几何法: )四 巩固练习
(1)已知圆C的圆心在x轴上,并且过点A(-1,1)和B(1,3),求圆C的标准方程.
(2)求过A(-1,5),B(5,5),C(6,-2)点的圆的方程.
??五 合作探究 圆的定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆。 问题:符合其它条件的点组所成的图形会 是圆吗?五 合作探究 解:设点M的坐标为(x,y).依题有化简得M的轨迹方程是思考:距离之比取其它值,点M的轨迹方程还是圆吗??五 合作探究 思考:距离之比取其它值,点M的轨迹方程还是圆吗????分组探究???之比到其它值呢?数学历史文化阿波罗尼斯圆 在平面上给定相异两点A、B,设P点在同一平面上且满足PA/PB= λ, 当λ>0且λ≠1时,P点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆。这个结论称作阿波罗尼斯轨迹定理。(圆的第二定义)阿波罗尼斯
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名。他的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地。
六 课堂总结只有科学才是真学问,将来用处无穷!--毛泽东写给毛岸青的话一、圆的方程的二种形式二、如何求圆的方程三、了解阿波罗尼斯圆(圆的第二定义)
由条件知
解得
故所求圆的标准方程为
待定系数法 解法二:
解 线段OA的中点
弦OA的垂直平分线的斜率
线段OA的垂直平分线的方程为:
即
圆心C的坐标是方程组 的解
解得
半径为
即所求圆的标准方程为
弦OA的垂直平分线几何法(数形结合法)例1:(习题4.1A组3)已知圆C的圆心在直线x-2y-1=0上,并且经过原点和A(2,1),求圆C的标准方程.三 能力提升解法三:
∵ 圆心C在直线 上,
∴可设点C的坐标为
又∵该圆经过A,O两点,∴
∴
解得 ∴圆心坐标为
半径为
即所求圆的标准方程为
例1:(习题4.1A组3)已知圆C的圆心在直线x-2y-1=0上,并且经过原点和A(2,1),求圆C的标准方程.三 能力提升
求圆的标准方程的方法:
(1)待定系数法:
①设圆的标准方程为(x-a)2+(y-b)2=r2(r>0);
②由条件列方程(组)解得a,b,r的值;
③写出圆的标准方程
(2)直接法
①一般先从确定圆的两个要素入手,即先求出圆心的坐标和半径,再写出圆的标准方程.
②确定圆心和半径时,常用到中点坐标公式、两点间的距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点为圆心”等.
例题小结:(几何法: )四 巩固练习
(1)已知圆C的圆心在x轴上,并且过点A(-1,1)和B(1,3),求圆C的标准方程.
(2)求过A(-1,5),B(5,5),C(6,-2)点的圆的方程.
??五 合作探究 圆的定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆。 问题:符合其它条件的点组所成的图形会 是圆吗?五 合作探究 解:设点M的坐标为(x,y).依题有化简得M的轨迹方程是思考:距离之比取其它值,点M的轨迹方程还是圆吗??五 合作探究 思考:距离之比取其它值,点M的轨迹方程还是圆吗????分组探究???之比到其它值呢?数学历史文化阿波罗尼斯圆 在平面上给定相异两点A、B,设P点在同一平面上且满足PA/PB= λ, 当λ>0且λ≠1时,P点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆。这个结论称作阿波罗尼斯轨迹定理。(圆的第二定义)阿波罗尼斯
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名。他的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地。
六 课堂总结只有科学才是真学问,将来用处无穷!--毛泽东写给毛岸青的话一、圆的方程的二种形式二、如何求圆的方程三、了解阿波罗尼斯圆(圆的第二定义)
