冀教版八年级数学上册《第十七章特殊三角形》单元测试题含答案
文档属性
| 名称 | 冀教版八年级数学上册《第十七章特殊三角形》单元测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-14 00:00:15 | ||
图片预览

文档简介
第十七章 特殊三角形
一、选择题(每小题4分,共32分)
1.下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
2.长度为下列四组数据的线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4
C.3,4,5 D.4,5,6
3.如果一个等腰三角形的两边长分别是4 cm和5 cm,那么此三角形的周长是( )
A.13 cm B.14 cm
C.15 cm D.13 cm或14 cm
4.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形的个数是( )
A.4 B.5
C.6 D.7
5.如图,AC=BC=10 cm,∠B=15°,若AD⊥BD于点D,则AD的长为( )
A.3 cm B.4 cm
C.5 cm D.6 cm
6.在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,则△ABC的周长为( )
A.42 B.60 C.42或60 D.25
7.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11 B.5.5 C.7 D.3.5
8.如图,在Rt△ABC中,∠A=90°,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A出发以每秒2 cm的速度向点C运动,点P,Q同时出发,其中一个点到达端点时,另一个点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
A.2.5s B.3s C.3.5s D.4s
二、填空题(每小题4分,共24分)
9.若用反证法证明“三个内角不相等的三角形不是等腰三角形”,可先假设这个三角形是____________.
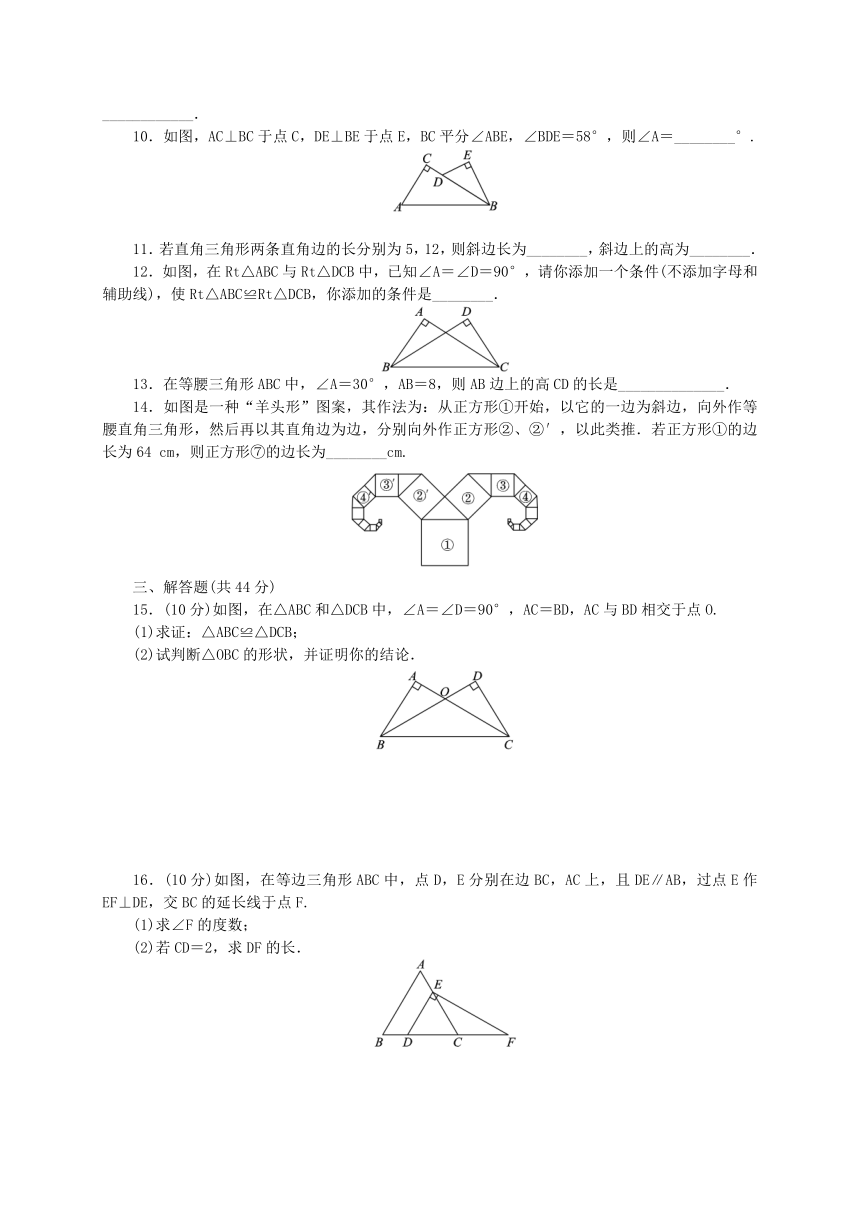
10.如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°,则∠A=________°.
11.若直角三角形两条直角边的长分别为5,12,则斜边长为________,斜边上的高为________.
12.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是________.
13.在等腰三角形ABC中,∠A=30°,AB=8,则AB边上的高CD的长是______________.
14.如图是一种“羊头形”图案,其作法为:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②、②′,以此类推.若正方形①的边长为64 cm,则正方形⑦的边长为________cm.
三、解答题(共44分)
15.(10分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)试判断△OBC的形状,并证明你的结论.
16.(10分)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
17.(12分)如图,已知锐角三角形ABC的两条高BE,CD相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
18.(12分)如图,△ABC是边长为6的等边三角形,P是AC边上一动点,Q是CB延长线上一动点,点P由点A向点C运动(与点A,C不重合),点Q同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)当∠BQD=30°时,求AP的长.
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果改变,请说明理由.
1.D 2.C 3.D 4.C 5.C 6.C 7.B 8.D
9.等腰三角形
10.58
11.13
12.答案不唯一,如AB=DC
13.4或4 或
14.8
15.解:(1)证明:在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL).
(2)△OBC是等腰三角形.
证明:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OC=OB,
∴△OBC是等腰三角形.
16.[解析] (1)根据平行线的性质可得∠EDC=∠B=60°,在Rt△DEF中,根据三角形内角和定理求解;(2)易证△EDC是等边三角形,再根据直角三角形的性质求解.
解:(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDF=90°-60°=30°.
(2)∵△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴DE=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
17.解:(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵BE,CD是△ABC的两条高,
∴∠CEB=∠BDC=90°.
又∵BC=CB,
∴△CEB≌△BDC(AAS),
∴∠DBC=∠ECB,∴AB=AC,∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:连接AO.由(1)得△BDC≌△CEB,∴DC=EB.
∵OC=OB,∴OD=OE.
又∵∠ADO=∠AEO=90°,AO=AO,∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,∴点O在∠BAC的平分线上.
18.解:(1)解法一:过点P作PF∥QC交AB于点F,则△AFP是等边三角形,∴AF=PF=AP.
∵点P,Q同时出发,且速度相同,∴BQ=AP,
∴BQ=PF.∵PF∥QC,∴∠FPD=∠DQB,∠PFD=∠DBQ,
∴△DBQ≌△DFP,∴BD=DF.
又易知∠BQD=∠BDQ=∠FDP=∠FPD=30°,
∴BD=DF=FA=AB=×6=2,∴AP=2.
解法二:∵点P,Q同时同速出发,∴AP=BQ.
设AP=BQ=x,则PC=6-x,QC=6+x.
在△QCP中,∠CQP=30°,∠C=60°,∴∠CPQ=90°,
∴QC=2PC,即6+x=2(6-x),解得x=2.∴AP=2.
(2)不变.
由(1)知BD=DF,而△APF是等边三角形,PE⊥AF,∴AE=EF.
又ED+(BD+AE)=AB=6,∴ED+(DF+EF)=6,
即ED+ED=6,∴ED=3为定值,即ED的长不变.
一、选择题(每小题4分,共32分)
1.下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
2.长度为下列四组数据的线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4
C.3,4,5 D.4,5,6
3.如果一个等腰三角形的两边长分别是4 cm和5 cm,那么此三角形的周长是( )
A.13 cm B.14 cm
C.15 cm D.13 cm或14 cm
4.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形的个数是( )
A.4 B.5
C.6 D.7
5.如图,AC=BC=10 cm,∠B=15°,若AD⊥BD于点D,则AD的长为( )
A.3 cm B.4 cm
C.5 cm D.6 cm
6.在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,则△ABC的周长为( )
A.42 B.60 C.42或60 D.25
7.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11 B.5.5 C.7 D.3.5
8.如图,在Rt△ABC中,∠A=90°,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A出发以每秒2 cm的速度向点C运动,点P,Q同时出发,其中一个点到达端点时,另一个点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
A.2.5s B.3s C.3.5s D.4s
二、填空题(每小题4分,共24分)
9.若用反证法证明“三个内角不相等的三角形不是等腰三角形”,可先假设这个三角形是____________.
10.如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°,则∠A=________°.
11.若直角三角形两条直角边的长分别为5,12,则斜边长为________,斜边上的高为________.
12.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是________.
13.在等腰三角形ABC中,∠A=30°,AB=8,则AB边上的高CD的长是______________.
14.如图是一种“羊头形”图案,其作法为:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②、②′,以此类推.若正方形①的边长为64 cm,则正方形⑦的边长为________cm.
三、解答题(共44分)
15.(10分)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)试判断△OBC的形状,并证明你的结论.
16.(10分)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
17.(12分)如图,已知锐角三角形ABC的两条高BE,CD相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
18.(12分)如图,△ABC是边长为6的等边三角形,P是AC边上一动点,Q是CB延长线上一动点,点P由点A向点C运动(与点A,C不重合),点Q同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)当∠BQD=30°时,求AP的长.
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果改变,请说明理由.
1.D 2.C 3.D 4.C 5.C 6.C 7.B 8.D
9.等腰三角形
10.58
11.13
12.答案不唯一,如AB=DC
13.4或4 或
14.8
15.解:(1)证明:在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL).
(2)△OBC是等腰三角形.
证明:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OC=OB,
∴△OBC是等腰三角形.
16.[解析] (1)根据平行线的性质可得∠EDC=∠B=60°,在Rt△DEF中,根据三角形内角和定理求解;(2)易证△EDC是等边三角形,再根据直角三角形的性质求解.
解:(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDF=90°-60°=30°.
(2)∵△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴DE=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
17.解:(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵BE,CD是△ABC的两条高,
∴∠CEB=∠BDC=90°.
又∵BC=CB,
∴△CEB≌△BDC(AAS),
∴∠DBC=∠ECB,∴AB=AC,∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:连接AO.由(1)得△BDC≌△CEB,∴DC=EB.
∵OC=OB,∴OD=OE.
又∵∠ADO=∠AEO=90°,AO=AO,∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,∴点O在∠BAC的平分线上.
18.解:(1)解法一:过点P作PF∥QC交AB于点F,则△AFP是等边三角形,∴AF=PF=AP.
∵点P,Q同时出发,且速度相同,∴BQ=AP,
∴BQ=PF.∵PF∥QC,∴∠FPD=∠DQB,∠PFD=∠DBQ,
∴△DBQ≌△DFP,∴BD=DF.
又易知∠BQD=∠BDQ=∠FDP=∠FPD=30°,
∴BD=DF=FA=AB=×6=2,∴AP=2.
解法二:∵点P,Q同时同速出发,∴AP=BQ.
设AP=BQ=x,则PC=6-x,QC=6+x.
在△QCP中,∠CQP=30°,∠C=60°,∴∠CPQ=90°,
∴QC=2PC,即6+x=2(6-x),解得x=2.∴AP=2.
(2)不变.
由(1)知BD=DF,而△APF是等边三角形,PE⊥AF,∴AE=EF.
又ED+(BD+AE)=AB=6,∴ED+(DF+EF)=6,
即ED+ED=6,∴ED=3为定值,即ED的长不变.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
