高中物理人教版选修3-5同步课件:16.4 碰撞40张PPT
文档属性
| 名称 | 高中物理人教版选修3-5同步课件:16.4 碰撞40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-08-15 09:39:49 | ||
图片预览










文档简介
课件40张PPT。4 碰撞第十六章 动量守恒定律知识探究典例精析达标检测1.理解弹性碰撞、非弹性碰撞,正碰(对心碰撞)和斜碰(非对心碰撞).
2.会应用动量、能量的观点综合分析、解决一维碰撞问题.
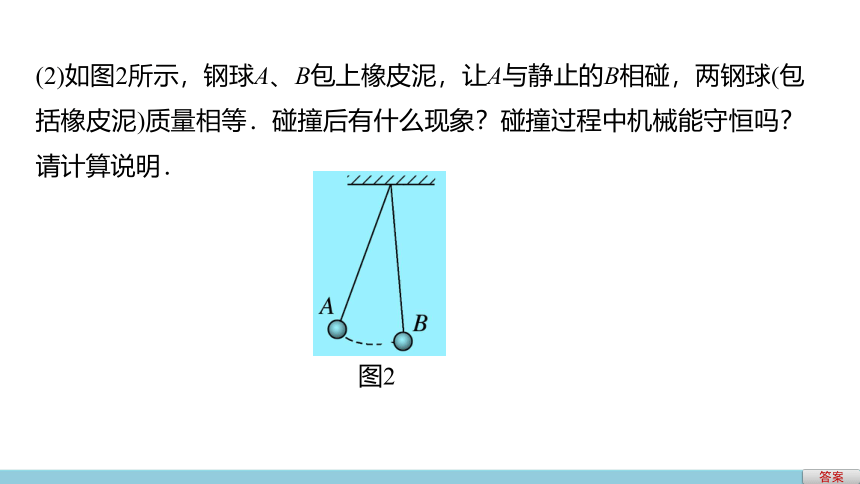
3.知道散射和中子的发现过程,体会理论对实践的指导作用,进一步了解动量守恒定律的普适性.一、弹性碰撞和非弹性碰撞(1)图1中大家正在玩一种游戏——超级碰撞球.多颗篮球般大小的钢球用钢缆悬挂在屋顶.拉开最右边钢球到某一高度,然后释放,碰撞后,仅最左边的球被弹起,摆至最大高度后落下来再次碰撞,致使最右边钢球又被弹起.硕大钢球交替弹开,周而复始,情景蔚为壮观.上述现象如何解释?知识探究导学探究图1答案答案 质量相等的两物体发生弹性正碰,碰后二者交换速度.答案(2)如图2所示,钢球A、B包上橡皮泥,让A与静止的B相碰,两钢球(包括橡皮泥)质量相等.碰撞后有什么现象?碰撞过程中机械能守恒吗?请计算说明.图2答案 碰撞后两球粘在一起,摆起高度减小.
设碰后两球粘在一起的速度为v′
由动量守恒定律知:mv=2mv′,则v′=
碰撞前总动能Ek= mv2
碰撞后总动能Ek′= ×2m( )2= mv2
所以碰撞过程中机械能减少
ΔEk=Ek-Ek′= mv2
即碰撞过程中机械能不守恒.弹性碰撞和非弹性碰撞的特点和规律
(1)碰撞特点:碰撞时间非常短;碰撞过程中内力远大于外力,系统所受外力可以忽略不计;可认为碰撞前后物体处于同一位置.
(2)弹性碰撞
①定义:如果碰撞过程中机械能 ,这样的碰撞叫做弹性碰撞.
②规律:
动量守恒:m1v1+m2v2=
机械能守恒:知识梳理答案守恒m1v1′+m2v2′(3)非弹性碰撞
①定义:如果碰撞过程中机械能 ,这样的碰撞叫做非弹性碰撞.
②规律:动量守恒:m1v1+m2v2=
机械能减少,损失的机械能转化为
|ΔEk|=Ek初-Ek末=Q
③完全非弹性碰撞
动量守恒:m1v1+m2v2=(m1+m2)v共
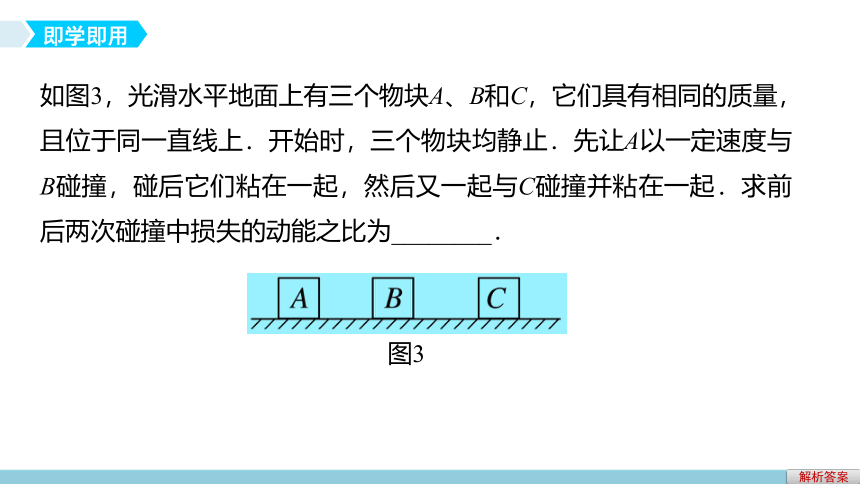
碰撞中机械能损失 答案不守恒m1v1′+m2v2′内能最多如图3,光滑水平地面上有三个物块A、B和C,它们具有相同的质量,且位于同一直线上.开始时,三个物块均静止.先让A以一定速度与B碰撞,碰后它们粘在一起,然后又一起与C碰撞并粘在一起.求前后两次碰撞中损失的动能之比为________.即学即用解析答案图3解析 设三个物块A、B和C的质量均为m,A与B碰撞前A的速度为v,碰撞后的速度为v1,A、B与C碰撞后的共同速度为v2.由动量守恒定律得
mv=2mv1
mv=3mv2
设第一次碰撞中的动能损失为ΔE1,第二次碰撞中的动能损失为ΔE2,由能量守恒定律得
联立以上四式解得ΔE1∶ΔE2=3∶1.
答案 3∶1二、对心碰撞和非对心碰撞、散射如图4所示为打台球的情景,质量相等的母球与目标球发生碰撞,有时碰后目标球的运动方向在碰前两球的球心连线上,有时不在连线上,这是什么原因?两个小球碰撞时一定交换速度吗?导学探究答案图4答案 有时发生的是对心碰撞,有时发生的是非对心碰撞.不一定,只有质量相等的两个物体发生一维弹性碰撞时,系统的总动量守恒,总动能守恒,才会交换速度,否则不会交换速度.对心碰撞、非对心碰撞和散射的理解
(1)正碰(对心碰撞):一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与 的连线在同一条直线上,碰撞之后两个球的速度仍会沿着 .
(2)斜碰(非对心碰撞):一个运动的球与一个静止的球碰撞,如果碰撞之前球的运动速度与 的连线不在同一条直线上,碰撞之后两球的速度都会偏离 .
(3)散射:微观粒子相互接近时并不像宏观物体那样“ ”,因此微观粒子的碰撞又叫做散射;发生散射时仍遵循 定律.答案知识梳理两球心这条直线两球心原来两球心的连线接触动量守恒(多选)对碰撞和散射的理解正确的是( )
A.两小球在光滑水平面上碰撞后粘在一起,因而不满足动量守恒定律
B.在系统所受合外力为零的条件下,正碰满足动量守恒定律,斜碰不满
足动量守恒定律
C.微观粒子碰撞时并不接触,但仍属于碰撞
D.微观粒子碰撞时虽不接触,但仍满足动量守恒定律即学即用解析答案返回解析 两小球在光滑水平面上的碰撞,小球相互作用时间很短,内力远大于外力,虽然粘在一起但系统的动量仍然守恒,故A错.
正碰、斜碰都满足动量守恒定律,故B错.
微观粒子在碰撞时虽然并不接触,但它具备碰撞的特点,即作用时间很短,作用力很大,运动状态变化明显,仍属于碰撞,并满足动量守恒定律,C、D正确.
答案 CD返回例1 在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,如图5所示.小球A与小球B发生正碰后小球A、B均向右运动.小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO.假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性碰撞,求两小球质量之比 .一、弹性碰撞模型及拓展分析典例精析图5解析答案总结提升解析 从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变,根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4∶1
两球碰撞过程为弹性碰撞,有:m1v0=m1v1+m2v2
解得 =2.
答案 2总结提升1.弹性碰撞遵循的规律:碰撞前后两物体动量守恒,动能守恒.
2.弹性碰撞模型特例:一动碰一静模型.
两质量分别为m1、m2的小球发生弹性正碰,v1≠0,v2=0,则有m1v1=m1v1′+m2v2′总结提升例2 (多选)质量为M的带有 光滑圆弧轨道的小车静止置于光滑水平面上,如图6所示,一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回小车的左端,则( )图6解析答案总结提升解析 小球上升到最高点时与小车相对静止,有相同的速度v′,由动量守恒定律和机械能守恒定律有:
Mv0=2Mv′ ①
②
联立①②得h= ,知D错误;
从小球滚上到滚下并离开小车,系统在水平方向上的动量守恒,由于无摩擦力做功,机械能守恒,此过程类似于弹性碰撞,作用后两者交换速度,即小球速度变为零,开始做自由落体运动,故B、C对,A错.答案 BC总结提升1.如果两个相互作用的物体,满足动量守恒的条件,且相互作用过程初、末状态的总机械能不变,广义上也可以看成是弹性碰撞.
2.本题可看成广义上的一动碰一静模型.小球滑上轨道时是“碰撞”的开始,小球离开轨道时是“碰撞”的结束.由于机械能守恒所以该过程类似于弹性碰撞,作用完成后小球和轨道交换速度.例3 冰球运动员甲的质量为80 kg.当他以5 m/s的速度向前运动时,与另一质量为100 kg、速度为3 m/s的迎面而来的运动员乙相撞.碰后甲恰好静止.假设碰撞时间极短,求:
(1)碰后乙的速度的大小;解析答案二、非弹簧碰撞模型分析解析 设运动员甲、乙的质量分别为m、M,碰前速度大小分别为v、v1,碰后乙的速度大小为v1′.设碰前运动员甲的速度方向为正方向.由动量守恒定律有
mv-Mv1=Mv1′
代入数据得v1′=1 m/s ①
答案 1 m/s (2)碰撞中总机械能的损失.解析答案总结提升解析 设碰撞过程中总机械能的损失为ΔE,应有
②
联立①②式,代入数据得ΔE=1 400 J.
答案 1 400 J 1.在碰撞过程中,系统的动量守恒,但机械能不一定守恒.
2.完全非弹性碰撞(碰后两物体粘在一起)机械能一定损失(机械能损失最多).
3.在爆炸过程中动量守恒,机械能一定不守恒(机械能增加).例4 质量为m、速度为v的A球跟质量为3m、静止的B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度允许有不同的值.请你论证:碰撞后B球的速度可能是以下值中的( )
A.0.6v B.0.4v
C.0.2v D.0.1v解析答案总结提升返回解析 若发生弹性碰撞,设碰后A的速度为v1,B的速度为v2,以A的初速度方向为正方向,由动量守恒定律:mv=mv1+3mv2
由机械能守恒定律:
若碰撞过程中损失机械能最大,则碰后两者速度相同,设为v′,由动量守恒定律:
mv=(m+3m)v′解析答案总结提升解得v′=
所以在情况不明确时,B球速度vB应满足
因此选B.
答案 B 总结提升返回1.现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生了碰撞.已知碰撞后,甲滑块静止不动,那么这次碰撞是( )
A.弹性碰撞 B.非弹性碰撞
C.完全非弹性碰撞 D.条件不足,无法确定达标检测1234解析答案解析 以甲滑块的运动方向为正方向,由动量守恒定律得:3m·v-mv=0+mv′,
所以v′=2v
碰前总动能
Ek= ×3m·v2+ mv2=2mv2
碰后总动能Ek′= mv′2=2mv2,
Ek=Ek′,所以A正确.
答案 A12342.在光滑的水平面上有三个完全相同的小球,它们成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们,如图7所示.设碰撞中不损失机械能,则碰后三个小球的速度可能值是( )1234图7A.v1=v2=v3= v0
B.v1=0,v2=v3= v0
C.v1=0,v2=v3= v0
D.v1=v2=0,v3=v0解析答案解析 两个质量相等的小球发生弹性正碰,碰撞过程中动量守恒,动能守恒,碰撞后将交换速度,故D项正确.
答案 D12343.(多选)A、B两个质量相等的球在光滑水平面上沿同一直线、同一方向运动,A球的动量是7 kg·m/s,B球的动量是5 kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能值是( )
A.pA′=8 kg·m/s,pB′=4 kg·m/s
B.pA′=6 kg·m/s,pB′=6 kg·m/s
C.pA′=5 kg·m/s,pB′=7 kg·m/s
D.pA′=-2 kg·m/s,pB′=14 kg·m/s1234解析答案解析 从动量守恒的角度分析,四个选项都正确;
从能量角度分析,A、B碰撞过程中没有其他形式的能量转化为它们的动能,所以碰撞后它们的总动能不能增加.碰前B在前,A在后,碰后如果二者同向,一定仍是B在前,A在后,A不可能超越B,所以碰后A的速度应小于等于B的速度.
A选项中,显然碰后A的速度大于B的速度,这是不符合实际情况的,所以A错.1234解析答案碰前A、B的总动能Ek=
碰后A、B的总动能,B选项中 所以B可能.
C选项中 故C也可能.
D选项中 所以D是不可能的.
综上,本题正确选项为B、C.
答案 BC 12344.质量分别为300 g和200 g的两个物体在无摩擦的水平面上相向运动,速度分别为50 cm/s和100 cm/s.
(1)如果两物体碰撞并粘合在一起,求它们共同的速度大小及碰撞中损失的动能.1234解析答案1234解析 令v1=50 cm/s=0.5 m/s,
v2=-100 cm/s=-1 m/s,
设两物体碰撞后粘合在一起的共同速度为v,
由动量守恒定律得m1v1+m2v2=(m1+m2)v,
代入数据解得v=-0.1 m/s,负号表示方向与v1的方向相反.
碰撞后两物体损失的动能为
答案 0.1 m/s 0.135 J(2)如果碰撞是弹性碰撞,求两物体碰撞后的速度大小.1234解析答案返回解析 如果碰撞是弹性碰撞,设碰后两物体的速度分别为v1′、v2′,
由动量守恒定律得m1v1+m2v2=m1v1′+m2v2′,
由机械能守恒定律得 代入数据得v1′=-0.7 m/s,v2′=0.8 m/s.
答案 0.7 m/s 0.8 m/s本课结束
2.会应用动量、能量的观点综合分析、解决一维碰撞问题.
3.知道散射和中子的发现过程,体会理论对实践的指导作用,进一步了解动量守恒定律的普适性.一、弹性碰撞和非弹性碰撞(1)图1中大家正在玩一种游戏——超级碰撞球.多颗篮球般大小的钢球用钢缆悬挂在屋顶.拉开最右边钢球到某一高度,然后释放,碰撞后,仅最左边的球被弹起,摆至最大高度后落下来再次碰撞,致使最右边钢球又被弹起.硕大钢球交替弹开,周而复始,情景蔚为壮观.上述现象如何解释?知识探究导学探究图1答案答案 质量相等的两物体发生弹性正碰,碰后二者交换速度.答案(2)如图2所示,钢球A、B包上橡皮泥,让A与静止的B相碰,两钢球(包括橡皮泥)质量相等.碰撞后有什么现象?碰撞过程中机械能守恒吗?请计算说明.图2答案 碰撞后两球粘在一起,摆起高度减小.
设碰后两球粘在一起的速度为v′
由动量守恒定律知:mv=2mv′,则v′=
碰撞前总动能Ek= mv2
碰撞后总动能Ek′= ×2m( )2= mv2
所以碰撞过程中机械能减少
ΔEk=Ek-Ek′= mv2
即碰撞过程中机械能不守恒.弹性碰撞和非弹性碰撞的特点和规律
(1)碰撞特点:碰撞时间非常短;碰撞过程中内力远大于外力,系统所受外力可以忽略不计;可认为碰撞前后物体处于同一位置.
(2)弹性碰撞
①定义:如果碰撞过程中机械能 ,这样的碰撞叫做弹性碰撞.
②规律:
动量守恒:m1v1+m2v2=
机械能守恒:知识梳理答案守恒m1v1′+m2v2′(3)非弹性碰撞
①定义:如果碰撞过程中机械能 ,这样的碰撞叫做非弹性碰撞.
②规律:动量守恒:m1v1+m2v2=
机械能减少,损失的机械能转化为
|ΔEk|=Ek初-Ek末=Q
③完全非弹性碰撞
动量守恒:m1v1+m2v2=(m1+m2)v共
碰撞中机械能损失 答案不守恒m1v1′+m2v2′内能最多如图3,光滑水平地面上有三个物块A、B和C,它们具有相同的质量,且位于同一直线上.开始时,三个物块均静止.先让A以一定速度与B碰撞,碰后它们粘在一起,然后又一起与C碰撞并粘在一起.求前后两次碰撞中损失的动能之比为________.即学即用解析答案图3解析 设三个物块A、B和C的质量均为m,A与B碰撞前A的速度为v,碰撞后的速度为v1,A、B与C碰撞后的共同速度为v2.由动量守恒定律得
mv=2mv1
mv=3mv2
设第一次碰撞中的动能损失为ΔE1,第二次碰撞中的动能损失为ΔE2,由能量守恒定律得
联立以上四式解得ΔE1∶ΔE2=3∶1.
答案 3∶1二、对心碰撞和非对心碰撞、散射如图4所示为打台球的情景,质量相等的母球与目标球发生碰撞,有时碰后目标球的运动方向在碰前两球的球心连线上,有时不在连线上,这是什么原因?两个小球碰撞时一定交换速度吗?导学探究答案图4答案 有时发生的是对心碰撞,有时发生的是非对心碰撞.不一定,只有质量相等的两个物体发生一维弹性碰撞时,系统的总动量守恒,总动能守恒,才会交换速度,否则不会交换速度.对心碰撞、非对心碰撞和散射的理解
(1)正碰(对心碰撞):一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与 的连线在同一条直线上,碰撞之后两个球的速度仍会沿着 .
(2)斜碰(非对心碰撞):一个运动的球与一个静止的球碰撞,如果碰撞之前球的运动速度与 的连线不在同一条直线上,碰撞之后两球的速度都会偏离 .
(3)散射:微观粒子相互接近时并不像宏观物体那样“ ”,因此微观粒子的碰撞又叫做散射;发生散射时仍遵循 定律.答案知识梳理两球心这条直线两球心原来两球心的连线接触动量守恒(多选)对碰撞和散射的理解正确的是( )
A.两小球在光滑水平面上碰撞后粘在一起,因而不满足动量守恒定律
B.在系统所受合外力为零的条件下,正碰满足动量守恒定律,斜碰不满
足动量守恒定律
C.微观粒子碰撞时并不接触,但仍属于碰撞
D.微观粒子碰撞时虽不接触,但仍满足动量守恒定律即学即用解析答案返回解析 两小球在光滑水平面上的碰撞,小球相互作用时间很短,内力远大于外力,虽然粘在一起但系统的动量仍然守恒,故A错.
正碰、斜碰都满足动量守恒定律,故B错.
微观粒子在碰撞时虽然并不接触,但它具备碰撞的特点,即作用时间很短,作用力很大,运动状态变化明显,仍属于碰撞,并满足动量守恒定律,C、D正确.
答案 CD返回例1 在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,如图5所示.小球A与小球B发生正碰后小球A、B均向右运动.小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO.假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性碰撞,求两小球质量之比 .一、弹性碰撞模型及拓展分析典例精析图5解析答案总结提升解析 从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变,根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4∶1
两球碰撞过程为弹性碰撞,有:m1v0=m1v1+m2v2
解得 =2.
答案 2总结提升1.弹性碰撞遵循的规律:碰撞前后两物体动量守恒,动能守恒.
2.弹性碰撞模型特例:一动碰一静模型.
两质量分别为m1、m2的小球发生弹性正碰,v1≠0,v2=0,则有m1v1=m1v1′+m2v2′总结提升例2 (多选)质量为M的带有 光滑圆弧轨道的小车静止置于光滑水平面上,如图6所示,一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回小车的左端,则( )图6解析答案总结提升解析 小球上升到最高点时与小车相对静止,有相同的速度v′,由动量守恒定律和机械能守恒定律有:
Mv0=2Mv′ ①
②
联立①②得h= ,知D错误;
从小球滚上到滚下并离开小车,系统在水平方向上的动量守恒,由于无摩擦力做功,机械能守恒,此过程类似于弹性碰撞,作用后两者交换速度,即小球速度变为零,开始做自由落体运动,故B、C对,A错.答案 BC总结提升1.如果两个相互作用的物体,满足动量守恒的条件,且相互作用过程初、末状态的总机械能不变,广义上也可以看成是弹性碰撞.
2.本题可看成广义上的一动碰一静模型.小球滑上轨道时是“碰撞”的开始,小球离开轨道时是“碰撞”的结束.由于机械能守恒所以该过程类似于弹性碰撞,作用完成后小球和轨道交换速度.例3 冰球运动员甲的质量为80 kg.当他以5 m/s的速度向前运动时,与另一质量为100 kg、速度为3 m/s的迎面而来的运动员乙相撞.碰后甲恰好静止.假设碰撞时间极短,求:
(1)碰后乙的速度的大小;解析答案二、非弹簧碰撞模型分析解析 设运动员甲、乙的质量分别为m、M,碰前速度大小分别为v、v1,碰后乙的速度大小为v1′.设碰前运动员甲的速度方向为正方向.由动量守恒定律有
mv-Mv1=Mv1′
代入数据得v1′=1 m/s ①
答案 1 m/s (2)碰撞中总机械能的损失.解析答案总结提升解析 设碰撞过程中总机械能的损失为ΔE,应有
②
联立①②式,代入数据得ΔE=1 400 J.
答案 1 400 J 1.在碰撞过程中,系统的动量守恒,但机械能不一定守恒.
2.完全非弹性碰撞(碰后两物体粘在一起)机械能一定损失(机械能损失最多).
3.在爆炸过程中动量守恒,机械能一定不守恒(机械能增加).例4 质量为m、速度为v的A球跟质量为3m、静止的B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度允许有不同的值.请你论证:碰撞后B球的速度可能是以下值中的( )
A.0.6v B.0.4v
C.0.2v D.0.1v解析答案总结提升返回解析 若发生弹性碰撞,设碰后A的速度为v1,B的速度为v2,以A的初速度方向为正方向,由动量守恒定律:mv=mv1+3mv2
由机械能守恒定律:
若碰撞过程中损失机械能最大,则碰后两者速度相同,设为v′,由动量守恒定律:
mv=(m+3m)v′解析答案总结提升解得v′=
所以在情况不明确时,B球速度vB应满足
因此选B.
答案 B 总结提升返回1.现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生了碰撞.已知碰撞后,甲滑块静止不动,那么这次碰撞是( )
A.弹性碰撞 B.非弹性碰撞
C.完全非弹性碰撞 D.条件不足,无法确定达标检测1234解析答案解析 以甲滑块的运动方向为正方向,由动量守恒定律得:3m·v-mv=0+mv′,
所以v′=2v
碰前总动能
Ek= ×3m·v2+ mv2=2mv2
碰后总动能Ek′= mv′2=2mv2,
Ek=Ek′,所以A正确.
答案 A12342.在光滑的水平面上有三个完全相同的小球,它们成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们,如图7所示.设碰撞中不损失机械能,则碰后三个小球的速度可能值是( )1234图7A.v1=v2=v3= v0
B.v1=0,v2=v3= v0
C.v1=0,v2=v3= v0
D.v1=v2=0,v3=v0解析答案解析 两个质量相等的小球发生弹性正碰,碰撞过程中动量守恒,动能守恒,碰撞后将交换速度,故D项正确.
答案 D12343.(多选)A、B两个质量相等的球在光滑水平面上沿同一直线、同一方向运动,A球的动量是7 kg·m/s,B球的动量是5 kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能值是( )
A.pA′=8 kg·m/s,pB′=4 kg·m/s
B.pA′=6 kg·m/s,pB′=6 kg·m/s
C.pA′=5 kg·m/s,pB′=7 kg·m/s
D.pA′=-2 kg·m/s,pB′=14 kg·m/s1234解析答案解析 从动量守恒的角度分析,四个选项都正确;
从能量角度分析,A、B碰撞过程中没有其他形式的能量转化为它们的动能,所以碰撞后它们的总动能不能增加.碰前B在前,A在后,碰后如果二者同向,一定仍是B在前,A在后,A不可能超越B,所以碰后A的速度应小于等于B的速度.
A选项中,显然碰后A的速度大于B的速度,这是不符合实际情况的,所以A错.1234解析答案碰前A、B的总动能Ek=
碰后A、B的总动能,B选项中 所以B可能.
C选项中 故C也可能.
D选项中 所以D是不可能的.
综上,本题正确选项为B、C.
答案 BC 12344.质量分别为300 g和200 g的两个物体在无摩擦的水平面上相向运动,速度分别为50 cm/s和100 cm/s.
(1)如果两物体碰撞并粘合在一起,求它们共同的速度大小及碰撞中损失的动能.1234解析答案1234解析 令v1=50 cm/s=0.5 m/s,
v2=-100 cm/s=-1 m/s,
设两物体碰撞后粘合在一起的共同速度为v,
由动量守恒定律得m1v1+m2v2=(m1+m2)v,
代入数据解得v=-0.1 m/s,负号表示方向与v1的方向相反.
碰撞后两物体损失的动能为
答案 0.1 m/s 0.135 J(2)如果碰撞是弹性碰撞,求两物体碰撞后的速度大小.1234解析答案返回解析 如果碰撞是弹性碰撞,设碰后两物体的速度分别为v1′、v2′,
由动量守恒定律得m1v1+m2v2=m1v1′+m2v2′,
由机械能守恒定律得 代入数据得v1′=-0.7 m/s,v2′=0.8 m/s.
答案 0.7 m/s 0.8 m/s本课结束
