概率小结
图片预览








文档简介
课件38张PPT。普通高中课程标准实验教科书(必修)数学3第三章 概率小结试验古典概型(2)每个基本事件出现的 可能性相等.(1)试验中所有可能出现的基本事件只有有限个;重点知识回顾 游戏规则:同时投掷两颗骰子,观察两颗骰子得到的点数和.如果点数和是 5,6,7,8,9 则老师赢,如果点数和是2,3,4,10,11,12则学生赢.一、古典概型老师赢的概率是多少呢?的特点:列表法 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
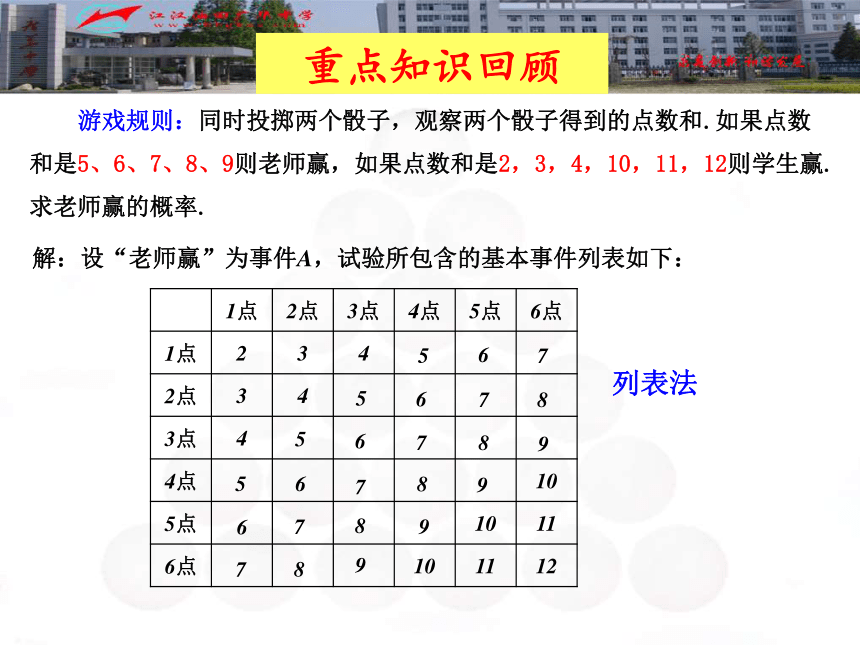
求老师赢的概率.解:设“老师赢”为事件A,试验所包含的基本事件列表如下:重点知识回顾列表法 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
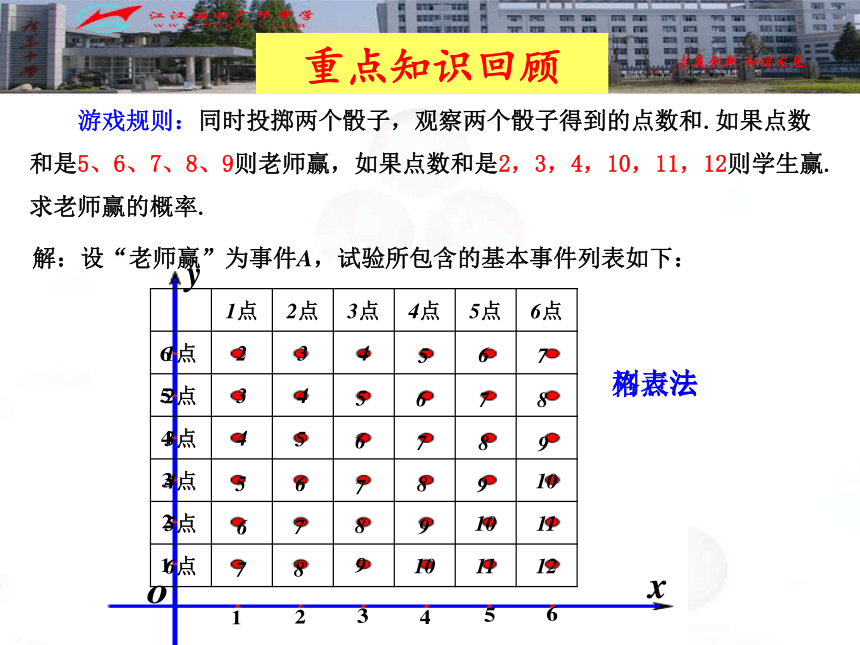
求老师赢的概率.解:设“老师赢”为事件A,试验所包含的基本事件列表如下:重点知识回顾格点法树状图法重点知识回顾解:设“老师赢”为事件A,试验所包含的基本事件列表如下: 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
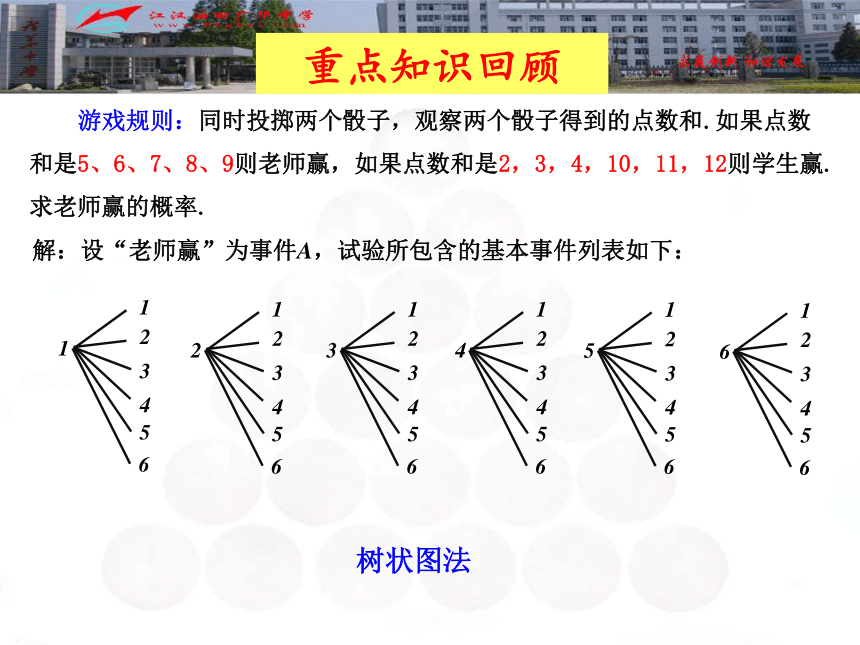
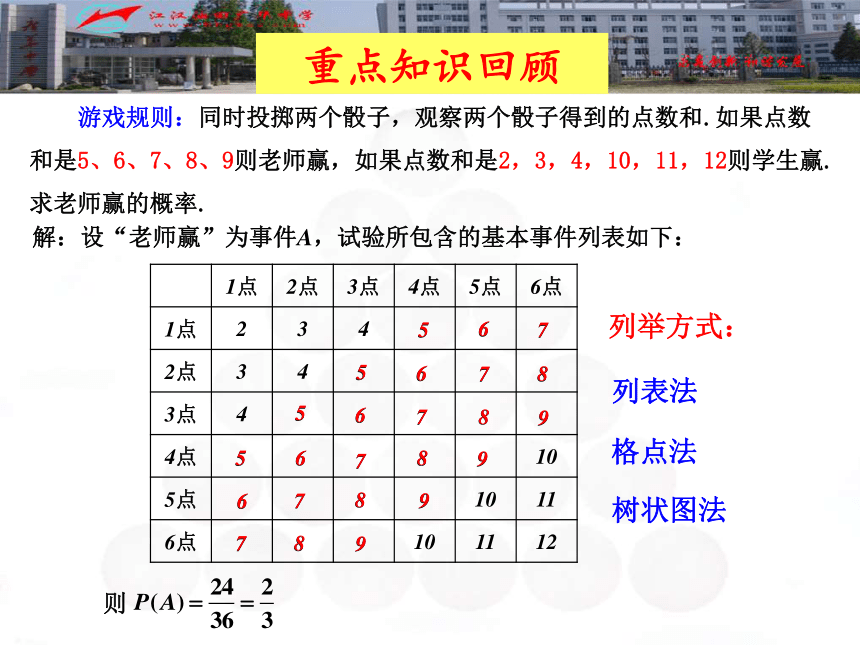
求老师赢的概率.列举方式:树状图法列表法重点知识回顾解:设“老师赢”为事件A,试验所包含的基本事件列表如下: 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
求老师赢的概率.格点法思考:随机事件发生的频率和概率有什么区别与联系?联系:频率是概率的近似值,随着试验次数的增加,频率会越
来越接近概率.区别:频率本身是随机的,在试验前不能确定,与每次试验有关;
概率是一个确定的数,是客观存在的,与每次试验无关.重点知识回顾 游戏规则:同时投掷两颗骰子,观察两颗骰子得到的点数和;如果是 5,6,7,8,9 则老师赢,如果是2,3,4,10,11,12则学生赢.重点知识回顾 游戏规则:同时投掷两颗骰子,观察两颗骰子得到的点数和;如果是 5,6,7,8,9 则老师赢,如果是2,3,4,10,11,12则学生赢.重点知识回顾(2)每个基本事件出现的可能性相等.(1)试验中所有可能出现的基本事件有无限个;几何概型变式:重点知识回顾二、几何概型的特点:重点知识回顾(1)请说出试验的一个基本事件;
(2)试验的所有基本事件构成了什么区域?
(3)如何计算该事件的概率?作出如图所示的平面区域,数形结合思想重点知识回顾试验中所有可能出现的基本事件有有限个试验中所有可能出现的基本事件有无限个每个基本事件出
现的可能性相等概率模型古典概型几何概型相同点重点知识回顾思考:求随机事件的概率的步骤是什么?(1)理解题意,弄清试验和事件(2)判断问题所属的概率模型(3)运用公式求随机事件的概率重点知识回顾 分类转化 小明和小红两个好朋友来荆门石油化工总厂应聘工作,他们一路过关斩将和另外3名应聘者一起进入了最后一轮面试.可是该公司只招聘3个人,假设这5个人被录用的机会相等.
(1)列出该公司招聘的所有可能结果;
(2) 小明和小红至少有一个被录用. 该试验所包含的基本事件有{A,B,C},{A,B,D}
{A,B,E},{A,C,D},{A,C,E},{A,D,E},
{B,C,D},{B,C,E}, {B,D,E},{C,D,E}. 解:(1)记小明和小红分别为A、B,其他的三名应聘者为C、D、E, 事件S“小明和小红都没有被录用”包含的结果为:
{C,D,E}
正难则反转化思想 (2)记“小明和小红至少有一个被录用”为事件Q,它的 对立事件“小明和小红都没有被录用” 为事件S.事件C“小明被录用小红不被录用”
事件D “小红被录用小明不被录用” 对立事件:两个事件在任何一次试验中有且只有一个发生.事件A “小明和小红至少有一个被录用”
事件B “小 明和小红都没有被录用” 互斥事件:两个事件在任何一次试验中不可能同时发生.特别地,事件A、B为对立事件,则对立事件一定是互斥事件,互斥事件不一定是对立事件.概率加法公式分类小结重点概念辨析解: (1)记小明和小红分别为A、B,其他的三名应聘者为C、D、E, 事件Q“小明和小红至少有一个被录用”包含的基本事件有9个.分类讨论思想{A,C,D}, { A,C,E}, {A,D,E}, {A,B,C}, {A,B,D},
{A,B,E}, {B,C,D}, {B,C,E}, {B,D,E}, (2)记“小明和小红至少有一个被录用” 为事件Q事件A“小明被录用小红不被录用”
事件B “小红被录用小明不被录用” 对立事件:两个事件在任何一次试验中有且只有一个发生.事件C“小明和小红至少有一个被录用”
事件D“小 明和小红都不被录用” 互斥事件:两个事件在任何一次试验中不可能同时发生.对立事件一定是互斥事件,互斥事件不一定是对立事件.特别地,事件A、B为对立事件,则概率加法公式转化小结重点概念辨析概率的意义与基本性质随机事件频 率随机数与随机模拟古典概型几何概型知识体系建构 1.从装有2个红球和2个黑球的口袋中取2个球,那么互斥
而不对立的两个事件是( ) CA、“至少有1个黑球”与“都是黑球”B、“至少有1个黑球”与“至少有1个红球”C、“恰有1个黑球”与“恰有2个黑球”D、“至少有1个黑球”与“都是红球”应用能力提升小结2作出如图所示的平面区域, (2)(b,c)可以看成平面内的点, 应用能力提升........................ 一个转盘分成4个全等的扇形,如图所示,转动的转盘自由停止时,指针指向扇形A的概率为多少?拓展探究同一个概率问题,有时候可以用不同的概率模型来解决.(1)课本P144 复习参考题
A组6,B组4.课后作业布置生活中很多事情的发生都是随机的,只要我们在人生路上脚踏实地、真心付出,那感受快乐的频率就会增多,成功的机会也会变大.
梦想的实现和破灭,也许是对立的,人生就是一次又一次的试验,但欣赏这一路的风景才是真正的快乐!或是古典概型,或是几何概型, 谢 谢!
求老师赢的概率.解:设“老师赢”为事件A,试验所包含的基本事件列表如下:重点知识回顾列表法 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
求老师赢的概率.解:设“老师赢”为事件A,试验所包含的基本事件列表如下:重点知识回顾格点法树状图法重点知识回顾解:设“老师赢”为事件A,试验所包含的基本事件列表如下: 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
求老师赢的概率.列举方式:树状图法列表法重点知识回顾解:设“老师赢”为事件A,试验所包含的基本事件列表如下: 游戏规则:同时投掷两个骰子,观察两个骰子得到的点数和.如果点数和是5、6、7、8、9则老师赢,如果点数和是2,3,4,10,11,12则学生赢.
求老师赢的概率.格点法思考:随机事件发生的频率和概率有什么区别与联系?联系:频率是概率的近似值,随着试验次数的增加,频率会越
来越接近概率.区别:频率本身是随机的,在试验前不能确定,与每次试验有关;
概率是一个确定的数,是客观存在的,与每次试验无关.重点知识回顾 游戏规则:同时投掷两颗骰子,观察两颗骰子得到的点数和;如果是 5,6,7,8,9 则老师赢,如果是2,3,4,10,11,12则学生赢.重点知识回顾 游戏规则:同时投掷两颗骰子,观察两颗骰子得到的点数和;如果是 5,6,7,8,9 则老师赢,如果是2,3,4,10,11,12则学生赢.重点知识回顾(2)每个基本事件出现的可能性相等.(1)试验中所有可能出现的基本事件有无限个;几何概型变式:重点知识回顾二、几何概型的特点:重点知识回顾(1)请说出试验的一个基本事件;
(2)试验的所有基本事件构成了什么区域?
(3)如何计算该事件的概率?作出如图所示的平面区域,数形结合思想重点知识回顾试验中所有可能出现的基本事件有有限个试验中所有可能出现的基本事件有无限个每个基本事件出
现的可能性相等概率模型古典概型几何概型相同点重点知识回顾思考:求随机事件的概率的步骤是什么?(1)理解题意,弄清试验和事件(2)判断问题所属的概率模型(3)运用公式求随机事件的概率重点知识回顾 分类转化 小明和小红两个好朋友来荆门石油化工总厂应聘工作,他们一路过关斩将和另外3名应聘者一起进入了最后一轮面试.可是该公司只招聘3个人,假设这5个人被录用的机会相等.
(1)列出该公司招聘的所有可能结果;
(2) 小明和小红至少有一个被录用. 该试验所包含的基本事件有{A,B,C},{A,B,D}
{A,B,E},{A,C,D},{A,C,E},{A,D,E},
{B,C,D},{B,C,E}, {B,D,E},{C,D,E}. 解:(1)记小明和小红分别为A、B,其他的三名应聘者为C、D、E, 事件S“小明和小红都没有被录用”包含的结果为:
{C,D,E}
正难则反转化思想 (2)记“小明和小红至少有一个被录用”为事件Q,它的 对立事件“小明和小红都没有被录用” 为事件S.事件C“小明被录用小红不被录用”
事件D “小红被录用小明不被录用” 对立事件:两个事件在任何一次试验中有且只有一个发生.事件A “小明和小红至少有一个被录用”
事件B “小 明和小红都没有被录用” 互斥事件:两个事件在任何一次试验中不可能同时发生.特别地,事件A、B为对立事件,则对立事件一定是互斥事件,互斥事件不一定是对立事件.概率加法公式分类小结重点概念辨析解: (1)记小明和小红分别为A、B,其他的三名应聘者为C、D、E, 事件Q“小明和小红至少有一个被录用”包含的基本事件有9个.分类讨论思想{A,C,D}, { A,C,E}, {A,D,E}, {A,B,C}, {A,B,D},
{A,B,E}, {B,C,D}, {B,C,E}, {B,D,E}, (2)记“小明和小红至少有一个被录用” 为事件Q事件A“小明被录用小红不被录用”
事件B “小红被录用小明不被录用” 对立事件:两个事件在任何一次试验中有且只有一个发生.事件C“小明和小红至少有一个被录用”
事件D“小 明和小红都不被录用” 互斥事件:两个事件在任何一次试验中不可能同时发生.对立事件一定是互斥事件,互斥事件不一定是对立事件.特别地,事件A、B为对立事件,则概率加法公式转化小结重点概念辨析概率的意义与基本性质随机事件频 率随机数与随机模拟古典概型几何概型知识体系建构 1.从装有2个红球和2个黑球的口袋中取2个球,那么互斥
而不对立的两个事件是( ) CA、“至少有1个黑球”与“都是黑球”B、“至少有1个黑球”与“至少有1个红球”C、“恰有1个黑球”与“恰有2个黑球”D、“至少有1个黑球”与“都是红球”应用能力提升小结2作出如图所示的平面区域, (2)(b,c)可以看成平面内的点, 应用能力提升........................ 一个转盘分成4个全等的扇形,如图所示,转动的转盘自由停止时,指针指向扇形A的概率为多少?拓展探究同一个概率问题,有时候可以用不同的概率模型来解决.(1)课本P144 复习参考题
A组6,B组4.课后作业布置生活中很多事情的发生都是随机的,只要我们在人生路上脚踏实地、真心付出,那感受快乐的频率就会增多,成功的机会也会变大.
梦想的实现和破灭,也许是对立的,人生就是一次又一次的试验,但欣赏这一路的风景才是真正的快乐!或是古典概型,或是几何概型, 谢 谢!
