探究与发现 函数y=Asin(ωx+φ)及函数y=Acos(ωx+φ)的周期
文档属性
| 名称 | 探究与发现 函数y=Asin(ωx+φ)及函数y=Acos(ωx+φ)的周期 |  | |
| 格式 | zip | ||
| 文件大小 | 806.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-18 10:44:26 | ||
图片预览




文档简介
课件15张PPT。探究与发现人教版A版 必修四第一章 三角函数 高一年级请回答:
今天星期三, 7天后星期几?
14天后呢?
84天后呢?
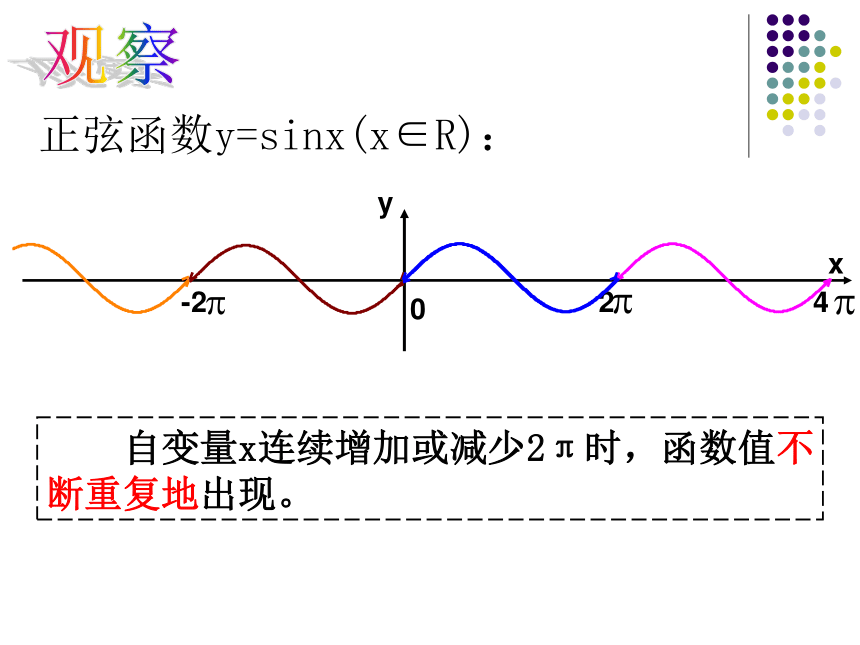
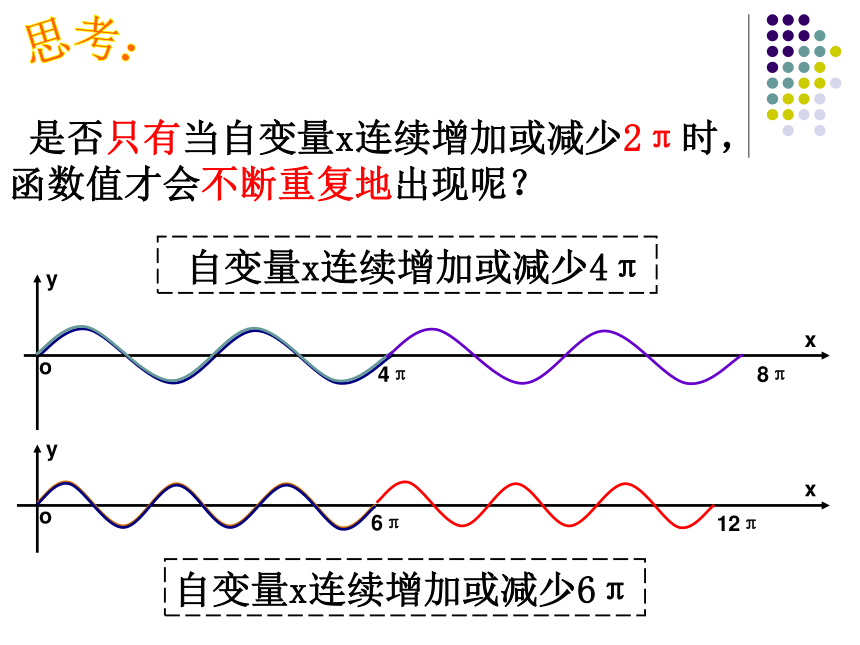
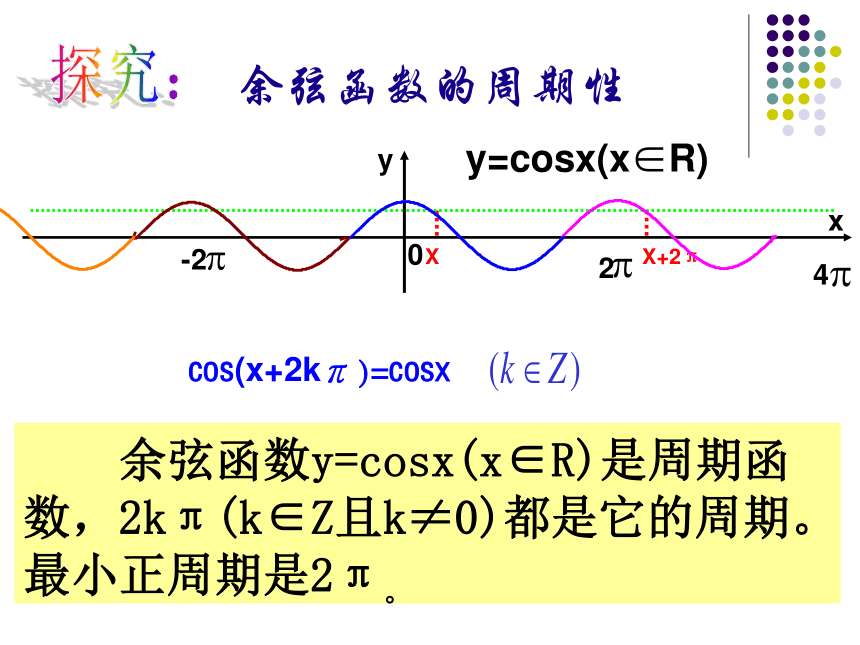
yx024-2正弦函数y=sinx(x∈R): 自变量x连续增加或减少2π时,函数值不断重复地出现。观察 是否只有当自变量x连续增加或减少2π时,函数值才会不断重复地出现呢?4π8π6π12π思考: 自变量x连续增加或减少4π自变量x连续增加或减少6π即:f(x+2kπ) =f(x)sin(x+ )=sinx2kπf(x+T)=f(x)当自变量x的值增加2π的整数倍时,函数值不变。 一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.周期函数定义: 正弦函数y=sinx(x∈R)是周期函数,2kπ(k∈Z且k≠0)都是它的周期。最小正周期是2π。正弦函数的周期性: 对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。最小正周期定义: 余弦函数y=cosx(x∈R)是周期函数,2kπ(k∈Z且k≠0)都是它的周期。最小正周期是2π。XX+2π024-2探究:余弦函数的周期性对于定义域中的每一个x,
f(x+T) =f(x) 恒成立。思考:周期函数:
存在一个
非零常数T,
对任意定义域内的x,都有
f(x+T)=f(x)
(1) T(T≠0)是f(x) 的周期,kT(k∈Z且k≠0)
是f(x) 的周期?(2) 是不是所有的周期函数都有最小正周期? 针对f(x+T) =f(x)中自变量x
本身所加的常量T才是周期。 周期函数的周期不止一个,若T是周期,则kT(k∈Z且k≠0)一定也是周期。 周期函数必有周期,但不一定有最小正周期。注意求下列函数的周期:
(1)y=3cosx(x∈R)(2)y=sin2x(x∈R)例题讲解:探究:练习:思考拓展提高6 1、周期函数的定义:f(x)=f(x+T),
最小正周期的定义 2、正弦函数和余弦函数都是周期函
数,2kπ(k∈Z且k≠0)都是它们的
周期。最小正周期是2π。小结:作业:必做题:《三维设计》选做题:思考
你认为我们应当如何利用函数的周期性来认识周期函数的其他性质?
今天星期三, 7天后星期几?
14天后呢?
84天后呢?
yx024-2正弦函数y=sinx(x∈R): 自变量x连续增加或减少2π时,函数值不断重复地出现。观察 是否只有当自变量x连续增加或减少2π时,函数值才会不断重复地出现呢?4π8π6π12π思考: 自变量x连续增加或减少4π自变量x连续增加或减少6π即:f(x+2kπ) =f(x)sin(x+ )=sinx2kπf(x+T)=f(x)当自变量x的值增加2π的整数倍时,函数值不变。 一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.周期函数定义: 正弦函数y=sinx(x∈R)是周期函数,2kπ(k∈Z且k≠0)都是它的周期。最小正周期是2π。正弦函数的周期性: 对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。最小正周期定义: 余弦函数y=cosx(x∈R)是周期函数,2kπ(k∈Z且k≠0)都是它的周期。最小正周期是2π。XX+2π024-2探究:余弦函数的周期性对于定义域中的每一个x,
f(x+T) =f(x) 恒成立。思考:周期函数:
存在一个
非零常数T,
对任意定义域内的x,都有
f(x+T)=f(x)
(1) T(T≠0)是f(x) 的周期,kT(k∈Z且k≠0)
是f(x) 的周期?(2) 是不是所有的周期函数都有最小正周期? 针对f(x+T) =f(x)中自变量x
本身所加的常量T才是周期。 周期函数的周期不止一个,若T是周期,则kT(k∈Z且k≠0)一定也是周期。 周期函数必有周期,但不一定有最小正周期。注意求下列函数的周期:
(1)y=3cosx(x∈R)(2)y=sin2x(x∈R)例题讲解:探究:练习:思考拓展提高6 1、周期函数的定义:f(x)=f(x+T),
最小正周期的定义 2、正弦函数和余弦函数都是周期函
数,2kπ(k∈Z且k≠0)都是它们的
周期。最小正周期是2π。小结:作业:必做题:《三维设计》选做题:思考
你认为我们应当如何利用函数的周期性来认识周期函数的其他性质?
