阅读与思考《三角学与天文学》
图片预览








文档简介
课件21张PPT。 阅读与思考:
三角学与天文学三角学与天文学 三角学的起源、发展与天文学密不可分,它是推算天文观察结果的一种方法,1450年以前的三角学主要是球面三角,在航海、历法推算、天文观测等实践活动中,后来测量、测绘工作的需要出现平面三角。三角学: 三角学是以研究三角形的边和角的关系为基础,测量为目的,也研究三角函数的性质及其应用的一门学科。
三角学分为平面三角学与球面三角学。都是研究三角形中边与角之间的关系。
平面三角学分:角的度量、三角函数与反三角函数、诱导公式、和与差的公式、倍角、半角公式、和差化积与积化和差公式、解三角形等内容;
球面三角学研究球面上由大圆弧构成的球面三角形的边与角之间的关系,在天文学、测量学、制图学、结晶学、仪器学等方面有广泛的应用。 雷格蒙塔努斯(Regiomontanus Johannes,1436—1476)德国数学家、天文学家。 弗朗索瓦·韦达(Fran?ois Viète,1540—1603)现代数学之父 约翰尼斯·开普勒(Johanns Kpler,1571—1630),杰出的德国天文学家尼古拉·哥白尼(Nicolaus Copernicus,1473—1543),文艺复兴时期波兰数学家、天文学家。向--为数学、天文学的发展
做出巨大贡献的数学家们致敬!对欧洲数学有推动作用数学家 在欧洲,最早将三角学从天文学中独立出来的数学家是德国人雷格蒙塔努斯,著作《论各种三角形》。2卷平面三角,明确使用正弦定理。3卷球面三角,给出球面三角的正弦定理和余弦定理。为三角学在平面、球面几何中的应用奠定了基础。对16世纪的数学家产生了极大影响。雷格蒙塔努斯三角学的发展 哥白尼的学生雷提库斯将传统的弧与弦的关系改进为角的三角函数关系,把三角函数定义为直角三角形的边的比,使平面三角从球面三角中独立出来,定义了正弦、余弦、正切、余切、正割、余割六个三角函数。大大推动了三角学的发展。尼古拉·哥白尼三角学的进一步发展 韦达将平面三角形和斜三角形的公式汇集在一起,补充了自己发现的正切公式,和差化积公式,将斜三角形中的问题转化为直角三角形的问题,平面三角与球面三角系统化工作,使三角学得到进一步发展。弗朗索瓦·韦达讨论、探索、思考:天文学问题
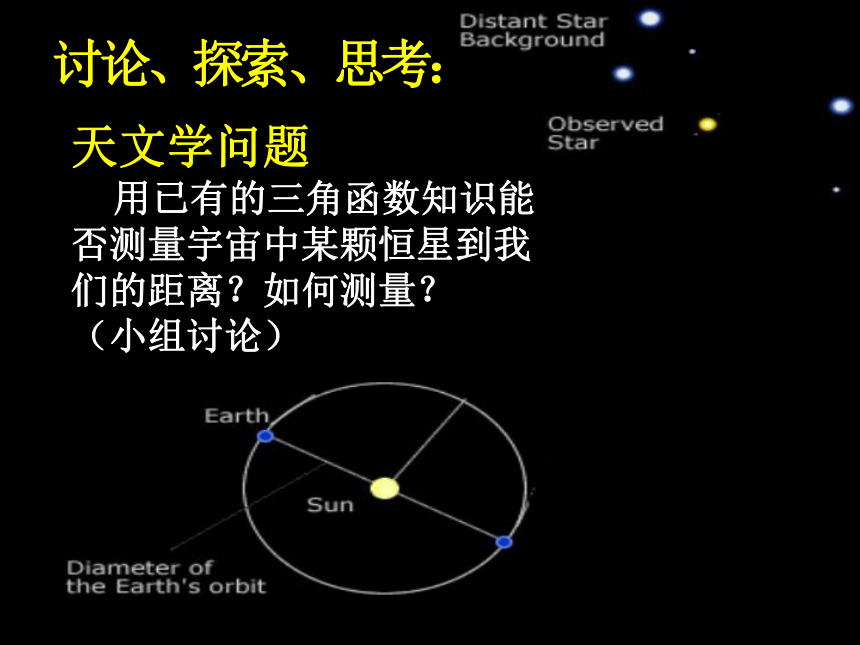
用已有的三角函数知识能否测量宇宙中某颗恒星到我们的距离?如何测量? (小组讨论)学生做:动手体验“视差” 伸出一只手指,分别闭上左、右眼看乔丹,会发现手指相对于背景物体的位置变动了,手指并没有移动,看起来相对于较远的背景有偏移,是因为观察的位置变动了,这就是生活中的“视差”。 Only two things are infinite – the universe and human stupidity, and I';m not sure about the former. - Albert Einstein 1838年,人类最早测定天体的距离的方法就是“视差法”。
在天文学上,观察者在地球上,以较远的星空为背景,观察一颗较近的恒星。由于地球位置的变动,观察者所见的较近的恒星相对于较远的星空背景就有了偏移。
三角视差在天文学中的应用天体测距·三角视差法
(秒差距) 恒星视差与距离 在地球上观测恒星的视差角是太阳、恒星与地球所形成的内角P,角P的倒数1/P叫秒差距秒差距 秒差距是天体距离的单位,是周年视差角P的倒数1/P。天体的视差角为1角秒时,
(1度=60角分=3600角秒),
它距离我们为1秒差距。
1秒差距=3.26光年。
应用实例:开普勒如何发现行星轨道 开普勒如何推出行星的“真实”轨道?人们不可能看到行星的真实运动,只能从运动着的地球上看到它们在天空的什么方向。假如轨道是匀速圆周运动,从地球上容易观察;可是地球本身同样是以某种未知方式绕太阳运动。说明不是圆周运动开普勒要研究天,先懂得地 ! 同哥白尼一样,敏锐地领悟到,“要研究天,先懂得地”,把着眼点放在地球的运动上,后研究行星的运动。多年积累的观测,分析研究,发现了行星沿椭圆轨道运行,并且提出了著名的开普勒三定律(轨道定律、面积定律、周期定律),为牛顿发现万有引力定律打下了基础。
开普勒 由近及远依次是:水星、金星、地球、火星、木星、土星、天王星、海王星。太阳系中的八大行星 十六世纪,三角学从天文学中分离出来,成为独立分支,后来,在微积分、物理学中有重要的应用。
课后作业:查阅三角学和天文学相关资料,了解数学对天文学的发展所起的作用。三角学和天文学分离
三角学与天文学三角学与天文学 三角学的起源、发展与天文学密不可分,它是推算天文观察结果的一种方法,1450年以前的三角学主要是球面三角,在航海、历法推算、天文观测等实践活动中,后来测量、测绘工作的需要出现平面三角。三角学: 三角学是以研究三角形的边和角的关系为基础,测量为目的,也研究三角函数的性质及其应用的一门学科。
三角学分为平面三角学与球面三角学。都是研究三角形中边与角之间的关系。
平面三角学分:角的度量、三角函数与反三角函数、诱导公式、和与差的公式、倍角、半角公式、和差化积与积化和差公式、解三角形等内容;
球面三角学研究球面上由大圆弧构成的球面三角形的边与角之间的关系,在天文学、测量学、制图学、结晶学、仪器学等方面有广泛的应用。 雷格蒙塔努斯(Regiomontanus Johannes,1436—1476)德国数学家、天文学家。 弗朗索瓦·韦达(Fran?ois Viète,1540—1603)现代数学之父 约翰尼斯·开普勒(Johanns Kpler,1571—1630),杰出的德国天文学家尼古拉·哥白尼(Nicolaus Copernicus,1473—1543),文艺复兴时期波兰数学家、天文学家。向--为数学、天文学的发展
做出巨大贡献的数学家们致敬!对欧洲数学有推动作用数学家 在欧洲,最早将三角学从天文学中独立出来的数学家是德国人雷格蒙塔努斯,著作《论各种三角形》。2卷平面三角,明确使用正弦定理。3卷球面三角,给出球面三角的正弦定理和余弦定理。为三角学在平面、球面几何中的应用奠定了基础。对16世纪的数学家产生了极大影响。雷格蒙塔努斯三角学的发展 哥白尼的学生雷提库斯将传统的弧与弦的关系改进为角的三角函数关系,把三角函数定义为直角三角形的边的比,使平面三角从球面三角中独立出来,定义了正弦、余弦、正切、余切、正割、余割六个三角函数。大大推动了三角学的发展。尼古拉·哥白尼三角学的进一步发展 韦达将平面三角形和斜三角形的公式汇集在一起,补充了自己发现的正切公式,和差化积公式,将斜三角形中的问题转化为直角三角形的问题,平面三角与球面三角系统化工作,使三角学得到进一步发展。弗朗索瓦·韦达讨论、探索、思考:天文学问题
用已有的三角函数知识能否测量宇宙中某颗恒星到我们的距离?如何测量? (小组讨论)学生做:动手体验“视差” 伸出一只手指,分别闭上左、右眼看乔丹,会发现手指相对于背景物体的位置变动了,手指并没有移动,看起来相对于较远的背景有偏移,是因为观察的位置变动了,这就是生活中的“视差”。 Only two things are infinite – the universe and human stupidity, and I';m not sure about the former. - Albert Einstein 1838年,人类最早测定天体的距离的方法就是“视差法”。
在天文学上,观察者在地球上,以较远的星空为背景,观察一颗较近的恒星。由于地球位置的变动,观察者所见的较近的恒星相对于较远的星空背景就有了偏移。
三角视差在天文学中的应用天体测距·三角视差法
(秒差距) 恒星视差与距离 在地球上观测恒星的视差角是太阳、恒星与地球所形成的内角P,角P的倒数1/P叫秒差距秒差距 秒差距是天体距离的单位,是周年视差角P的倒数1/P。天体的视差角为1角秒时,
(1度=60角分=3600角秒),
它距离我们为1秒差距。
1秒差距=3.26光年。
应用实例:开普勒如何发现行星轨道 开普勒如何推出行星的“真实”轨道?人们不可能看到行星的真实运动,只能从运动着的地球上看到它们在天空的什么方向。假如轨道是匀速圆周运动,从地球上容易观察;可是地球本身同样是以某种未知方式绕太阳运动。说明不是圆周运动开普勒要研究天,先懂得地 ! 同哥白尼一样,敏锐地领悟到,“要研究天,先懂得地”,把着眼点放在地球的运动上,后研究行星的运动。多年积累的观测,分析研究,发现了行星沿椭圆轨道运行,并且提出了著名的开普勒三定律(轨道定律、面积定律、周期定律),为牛顿发现万有引力定律打下了基础。
开普勒 由近及远依次是:水星、金星、地球、火星、木星、土星、天王星、海王星。太阳系中的八大行星 十六世纪,三角学从天文学中分离出来,成为独立分支,后来,在微积分、物理学中有重要的应用。
课后作业:查阅三角学和天文学相关资料,了解数学对天文学的发展所起的作用。三角学和天文学分离
