人教A版高中数学必修2第三章第一节直线的倾斜角与斜率(教师版+学生版)教师版
文档属性
| 名称 | 人教A版高中数学必修2第三章第一节直线的倾斜角与斜率(教师版+学生版)教师版 |
|
|
| 格式 | zip | ||
| 文件大小 | 96.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-18 00:00:00 | ||
图片预览

文档简介
解析几何初步
直线与直线方程
【学习目标】
学习重点:理解直线的倾斜角和斜率的概念。
学习难点:过两点的直线斜率的计算公式的应用。
考点1 直线的确定及直线的倾斜角
阅读教材,完成下列问题:
直线的确定:在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的 和这条直线的 。
【答案:一个点,方向】
2. 直线的倾斜角:①定义:在平面直角坐标系中,对于一条与x轴相交的直线l,把 按 方向绕着交点旋转到和直线l 所成的角,叫作直线l的倾斜角,通常用α表示。②范围: 。
【答案:x轴(正方向),逆时针,重合,0°≤α<180°】
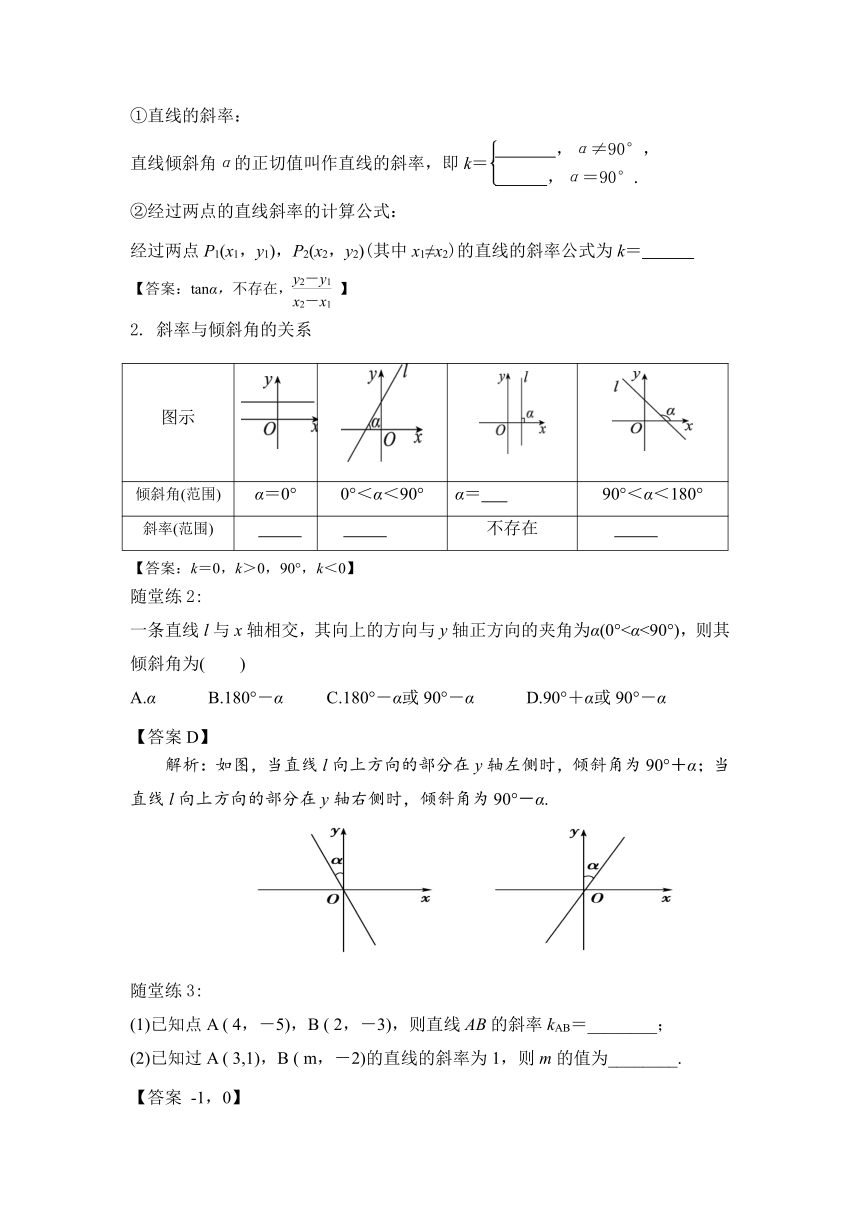
随堂练1:
如下图中标注的α表示直线l的倾斜角的是( )
A.① B.①② C.①③ D.②④
【答案A】
考点2 直线的斜率
阅读教材,完成下列问题:
1.直线的斜率与斜率的计算公式:
①直线的斜率:
直线倾斜角α的正切值叫作直线的斜率,即k=
②经过两点的直线斜率的计算公式:
经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2)的直线的斜率公式为k=
【答案:tanα,不存在, 】
2. 斜率与倾斜角的关系
图示
倾斜角(范围)
α=0°
0°<α<90°
α=
90°<α<180°
斜率(范围)
不存在
【答案:k=0,k>0,90°,k<0】
随堂练2:
一条直线l与x轴相交,其向上的方向与y轴正方向的夹角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α C.180°-α或90°-α D.90°+α或90°-α
【答案D】
解析:如图,当直线l向上方向的部分在y轴左侧时,倾斜角为90°+α;当直线l向上方向的部分在y轴右侧时,倾斜角为90°-α.
随堂练3:
(1)已知点A ( 4,-5),B ( 2,-3),则直线AB的斜率kAB=________;
(2)已知过A ( 3,1),B ( m,-2)的直线的斜率为1,则m的值为________.
【答案 -1,0】
解析:(1)kAB===-1.
(2)当m=3时,直线AB平行于y轴,斜率不存在.
当m≠3时,k==-=1,解得m=0.
【方法总结】
1、求直线倾斜角的方法及两点注意:
(1)方法:结合图形,构造含倾斜角的特殊三角形求解.
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°;②注意直线倾斜角的取值范围是0°≤α<180°.
2、求直线的斜率有两种思路:
当两点的横坐标相等时,过这两个点的直线与x轴垂直,其斜率不存在,不能用斜率公式求解,因此,用斜率公式求斜率时,要先判断斜率是否存在。求直线斜率的取值范围时,通常先结合图形找出倾斜角的范围,再得到斜率的范围。
利用斜率可解决点共线问题,点A,B,C共线?kAB=kAC或kAB与kAC都不存在。的几何意义是直线的斜率,用之可通过几何方法解决函数的值域问题。
课 时 作 业
1、设直线l与x轴交于点A,其倾斜角为α,直线l绕点A顺时针旋转45°后得直线l1,有下列四个选项:①α+45°;②α+135°;③α-45°;④135°-α,则直线l1的倾斜角可能的取值是( )
A.①② B.②③ C.③④ D.①④
【答案B】
解析:当α≥45°时,直线l绕点A顺时针旋转45°后得直线l1的倾斜角为α-45°;当0°≤α<45°时,直线l1的倾斜角为180°-(45°-α)=135°+α,故选B。
2、已知直线l经过两点P1(2,1)和P2(m,2)(m∈R)。
(1)求直线l的斜率;
(2)若直线l的倾斜角α为45°,求m的值。
【答案及解析】
(1)当m=2时,x1=x2=2,∴直线l垂直x轴,故直线l的斜率不存在.
当m≠2时,直线l的斜率k==.
(2)∵α=45°,∴k=tan α=1,
∴=1,即m-2=1,∴m=3.
3、若三点A(2,-3),B(4,3),C(5,k)在同一条直线上,求k的值。
【答案k=6】
解析 ∵A,B,C在同一条直线上,∴kAB = kBC ,
∴=,解得k=6。
4、已知坐标平面内三点A(-1,1),B(1,1),C(2,+1)。
(1)求直线AB,BC,AC的斜率和倾斜角;
(2)若D为△ABC的边AB上一动点,求直线CD斜率k的变化范围。
答案解析:(1)由斜率公式得:
kAB==0,kBC==,
kAC==.
∵tan 0°=0,∴AB的倾斜角为0°;
tan 60°=,∴BC的倾斜角为60°;
tan 30°=,∴AC的倾斜角为30°。
(2)如图,当斜率k变化时,直线CD绕C点旋转,当直线CD由CA逆时针转到CB时,直线CD与AB恒有交点,
即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围是.
5、已知点A(2,-3),B(-3,-2),直线l过点P(3,1)且与线段AB相交,求直线l的斜率的取值范围。
答案解析:如图所示,设直线l,PA,PB的倾斜角分别是α,α1,α2.
当l与线段AB相交时,有0<α2≤α≤α1<,则tan α2≤tan α≤tan α1,
∴kPB≤k≤kPA。又kPA==4,kPB==,∴≤k≤4,即直线l的斜率的取值范围是 。
6、如图,四边形OABC为等腰梯形,其中上底长为1,下底长为3,高为1,求梯形各边所在直线的倾斜角和斜率 。
答案解析:如图,分别过点B,C作x轴的垂线,垂足分别为D和E,则有OE=ED=DA=1,CE=BD=1,所以C(1,1),B(2,1),A(3,0),所以kOC==1,kOA=kBC=0,所以OA,BC,CO三边所在直线的倾斜角分别为0°,0°,45°.又OC与AB倾斜角互补,则直线AB的倾斜角为180°-45°=135°.
直线与直线方程
【学习目标】
学习重点:理解直线的倾斜角和斜率的概念。
学习难点:过两点的直线斜率的计算公式的应用。
考点1 直线的确定及直线的倾斜角
阅读教材,完成下列问题:
直线的确定:在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的 和这条直线的 。
【答案:一个点,方向】
2. 直线的倾斜角:①定义:在平面直角坐标系中,对于一条与x轴相交的直线l,把 按 方向绕着交点旋转到和直线l 所成的角,叫作直线l的倾斜角,通常用α表示。②范围: 。
【答案:x轴(正方向),逆时针,重合,0°≤α<180°】
随堂练1:
如下图中标注的α表示直线l的倾斜角的是( )
A.① B.①② C.①③ D.②④
【答案A】
考点2 直线的斜率
阅读教材,完成下列问题:
1.直线的斜率与斜率的计算公式:
①直线的斜率:
直线倾斜角α的正切值叫作直线的斜率,即k=
②经过两点的直线斜率的计算公式:
经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2)的直线的斜率公式为k=
【答案:tanα,不存在, 】
2. 斜率与倾斜角的关系
图示
倾斜角(范围)
α=0°
0°<α<90°
α=
90°<α<180°
斜率(范围)
不存在
【答案:k=0,k>0,90°,k<0】
随堂练2:
一条直线l与x轴相交,其向上的方向与y轴正方向的夹角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α C.180°-α或90°-α D.90°+α或90°-α
【答案D】
解析:如图,当直线l向上方向的部分在y轴左侧时,倾斜角为90°+α;当直线l向上方向的部分在y轴右侧时,倾斜角为90°-α.
随堂练3:
(1)已知点A ( 4,-5),B ( 2,-3),则直线AB的斜率kAB=________;
(2)已知过A ( 3,1),B ( m,-2)的直线的斜率为1,则m的值为________.
【答案 -1,0】
解析:(1)kAB===-1.
(2)当m=3时,直线AB平行于y轴,斜率不存在.
当m≠3时,k==-=1,解得m=0.
【方法总结】
1、求直线倾斜角的方法及两点注意:
(1)方法:结合图形,构造含倾斜角的特殊三角形求解.
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°;②注意直线倾斜角的取值范围是0°≤α<180°.
2、求直线的斜率有两种思路:
当两点的横坐标相等时,过这两个点的直线与x轴垂直,其斜率不存在,不能用斜率公式求解,因此,用斜率公式求斜率时,要先判断斜率是否存在。求直线斜率的取值范围时,通常先结合图形找出倾斜角的范围,再得到斜率的范围。
利用斜率可解决点共线问题,点A,B,C共线?kAB=kAC或kAB与kAC都不存在。的几何意义是直线的斜率,用之可通过几何方法解决函数的值域问题。
课 时 作 业
1、设直线l与x轴交于点A,其倾斜角为α,直线l绕点A顺时针旋转45°后得直线l1,有下列四个选项:①α+45°;②α+135°;③α-45°;④135°-α,则直线l1的倾斜角可能的取值是( )
A.①② B.②③ C.③④ D.①④
【答案B】
解析:当α≥45°时,直线l绕点A顺时针旋转45°后得直线l1的倾斜角为α-45°;当0°≤α<45°时,直线l1的倾斜角为180°-(45°-α)=135°+α,故选B。
2、已知直线l经过两点P1(2,1)和P2(m,2)(m∈R)。
(1)求直线l的斜率;
(2)若直线l的倾斜角α为45°,求m的值。
【答案及解析】
(1)当m=2时,x1=x2=2,∴直线l垂直x轴,故直线l的斜率不存在.
当m≠2时,直线l的斜率k==.
(2)∵α=45°,∴k=tan α=1,
∴=1,即m-2=1,∴m=3.
3、若三点A(2,-3),B(4,3),C(5,k)在同一条直线上,求k的值。
【答案k=6】
解析 ∵A,B,C在同一条直线上,∴kAB = kBC ,
∴=,解得k=6。
4、已知坐标平面内三点A(-1,1),B(1,1),C(2,+1)。
(1)求直线AB,BC,AC的斜率和倾斜角;
(2)若D为△ABC的边AB上一动点,求直线CD斜率k的变化范围。
答案解析:(1)由斜率公式得:
kAB==0,kBC==,
kAC==.
∵tan 0°=0,∴AB的倾斜角为0°;
tan 60°=,∴BC的倾斜角为60°;
tan 30°=,∴AC的倾斜角为30°。
(2)如图,当斜率k变化时,直线CD绕C点旋转,当直线CD由CA逆时针转到CB时,直线CD与AB恒有交点,
即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围是.
5、已知点A(2,-3),B(-3,-2),直线l过点P(3,1)且与线段AB相交,求直线l的斜率的取值范围。
答案解析:如图所示,设直线l,PA,PB的倾斜角分别是α,α1,α2.
当l与线段AB相交时,有0<α2≤α≤α1<,则tan α2≤tan α≤tan α1,
∴kPB≤k≤kPA。又kPA==4,kPB==,∴≤k≤4,即直线l的斜率的取值范围是 。
6、如图,四边形OABC为等腰梯形,其中上底长为1,下底长为3,高为1,求梯形各边所在直线的倾斜角和斜率 。
答案解析:如图,分别过点B,C作x轴的垂线,垂足分别为D和E,则有OE=ED=DA=1,CE=BD=1,所以C(1,1),B(2,1),A(3,0),所以kOC==1,kOA=kBC=0,所以OA,BC,CO三边所在直线的倾斜角分别为0°,0°,45°.又OC与AB倾斜角互补,则直线AB的倾斜角为180°-45°=135°.
