1.1.1 命题 课件
图片预览










文档简介
课件44张PPT。1.1.1命题 高二年级 数学
人教版 选修2-1
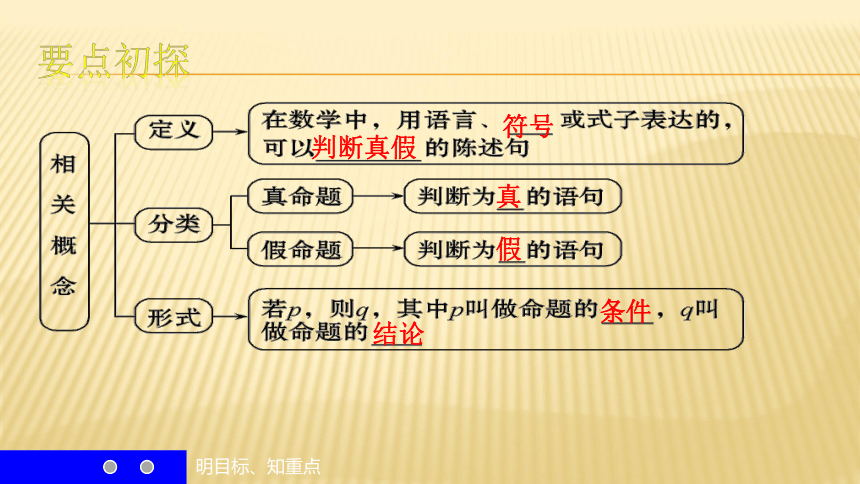
1.1.1 命 题自主学习1.命题的定义是什么?在定义中有哪些关键字?2.命题是如何分类的?3.研究了命题的哪种结构形式?要点初探符号判断真假真假条件结论Contents Page明目标知重点填要点
记疑点探要点
究所然内容
索引010203当堂测
查疑缺 041.理解命题的概念和命题的构成,能判断给定陈述句是否为命题.
2.能判断命题的真假.
3.能把命题改写成“若p,则q”的形式.明目标、知重点1.命题的定义
用 表达的,可以判断 的_______
叫做命题.
判断为 的语句叫做 .
判断为 的语句叫做 .填要点·记疑点语言、符号或式子真假陈述句真假真命题假命题2.命题的结构
从构成来看,所有的命题都由 两部分构成.在数学中,命题常写成 这种形式,通常,我们把这种形式的命题中的p叫做 ,q叫做
.条件和结论“若p,则q”命题的条件命题的结论探要点·究所然情境导学我们在初中已经学过许多数学命题,但还不适应我们今后学习的需要,本节开始我们深化对命题的研究.思考1 在初中,我们已学过许多数学命题,当时是如何定义命题的,你能举出一个例子吗?
答 判断一件事情的句子.例如,有两边相等的三角形是等腰三角形.探究点一 命题的定义思考2 下面语句的表述形式有什么特点?
(1)若直线a∥b,则直线a和直线b无公共点;
(2)2+4=7;
(3)平面内垂直于同一条直线的两条直线平行;
(4)若x2=1,则x=1;
(5)两个全等三角形的面积相等;
(6)3能被2整除.
答 都是陈述句,都能判断真假.思考3 数学中的定义、公理、定理、推论是命题吗?
答 是.
小结 用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.例1 判断下面的语句是不是命题.
(1)空集是任何集合的子集.
(2)若整数a是素数,则a是奇数.
(3)指数函数是增函数吗?
(4)若平面上两条直线不相交,则这两条直线平行.
(6)x>15.
解 (1)(2)(4)(5)是命题.(3)(6)不是命题.反思与感悟 并不是所有的语句都是命题,只有能判断真假的陈述句才是命题,命题首先是“陈述句”,其他语句如疑问句、祈使句、感叹句等一般都不是命题;其次是“能判断真假”,不能判断真假的陈述句不是命题,如“x≥2”、“小高的个子很高”等都不能判断真假,故都不是命题.
因此,判断一个语句是否为命题,关键有两点:①是否为陈述句;②能否判断真假.跟踪训练1 判断下列语句是不是命题.
(1)求证 是无理数.
(2)x2+2x+1≥0.
(3)你是高二学生吗?
(4)并非所有的人都喜欢吃苹果.
(5)一个正整数不是质数就是合数.
(6)若x∈R,则x2+4x+7>0.
(7)x+3>0.
解 (1)(3)(7)不是命题,(2)(4)(5)(6)是命题.思考1 命题分哪几类?
答 真命题和假命题.
小结 判断为真的语句叫做真命题;判断为假的语句叫做假命题.探究点二 命题的分类例2 请对例1给出的命题判断真假.
解 (1)(4)(5)是真命题,(2)是假命题.反思与感悟 要判断一个命题是真命题,一般需要经过严格的推理论证,在判断时,要有理有据,有时应综合各种情况作出正确的判断,而判断一个命题是假命题,只需举出一个反例即可.跟踪训练2 判断下列命题的真假:
(1)已知a,b,c,d∈R,若a≠c,b≠d,则a+b≠c+d;
解 假命题.反例:1≠4,5≠2,而1+5=4+2.(2)若x∈N,则x3>x2成立;
解 假命题.反例:当x=0时,x3>x2不成立.(3)若m>1,则方程x2-2x+m=0无实数根;
解 真命题:∵m>1?Δ=4-4m<0,∴方程x2-2x+m=0无实数根.(4)存在一个三角形没有外接圆.
解 假命题.因为不共线的三点确定一个圆,即任何三角形都有外接圆.思考2 数学中的定义、公理、定理、推论是真命题吗?
答 是.思考1 跟踪训练2中(2)(3)两个命题是什么形式?命题的常见形式是什么?
答 命题(2)(3)具有“若p,则q”的形式,即为命题的常见形式.探究点三 命题的结构小结 命题由条件和结论两部分组成,它的结构形式为:“若p,则q”.也可写成:“如果p,那么q.其中p是命题的条件,q是命题的结论.思考2 指出下列命题中的条件p和结论q:
(1)若整数a能被2整除,则整数a是偶数;
答 条件p:整数a能被2整除,
结论q:整数a是偶数.(2)若四边形是菱形,则它的对角线互相垂直且平分.
答 条件p:四边形是菱形,
结论q:四边形的对角线互相垂直且平分.思考3 如何把命题改写成“若p,则q”的形式.
答 分清条件和结论.例3 将下列命题改写成“若p,则q”的形式,并判断真假.
(1)垂直于同一条直线的两条直线平行;
解 若两条直线垂直于同一条直线,则这两条直线平行.假命题.(2)负数的立方是负数;
解 若一个数是负数,则这一个数的立方是负数.真命题.(3)对顶角相等.
解 若两个角是对顶角,则这两个角相等.真命题.反思与感悟 把一个命题改写成“若p,则q”的形式,首先要确定命题的条件和结论,若条件和结论比较隐含,要补充完整,有时一个条件有多个结论,有时一个结论需多个条件,还要注意有的命题改写形式也不唯一.跟踪训练3 把下列命题改写成“若p,则q”的形式,并判断真假.
(1)实数的平方是非负数;
解 若一个数是实数,则它的平方是非负数.真命题.(2)等底等高的两个三角形是全等三角形;
解 若两个三角形等底等高,则这两个三角形是全等三角形.假命题.(3)当ac>bc时,a>b;
解 若ac>bc,则a>b.假命题.(4)角的平分线上的点到角的两边的距离相等.
解 若一个点是一个角的平分线上的点,则该点到这个角的两边的距离相等.真命题.当堂测·查疑缺 12341.下列语句是命题的是( )
A.2 014是一个大数
B.若两直线平行,则这两条直线没有公共点
C.对数函数是增函数吗
D.a≤15
解析 A、D不能判断真假,不是命题;B能够判断真假而且是陈述句,是命题;C是疑问句,不是命题.B2.下列命题中是真命题的是( )
A.互余的两个角不相等
B.相等的两个角是同位角
C.若a2=b2,则|a|=|b|
D.三角形的一个外角等于和它不相邻的一个内角
解析 由平面几何知识可知A、B、D三项都是错误的.1234C12343.命题“函数y=2x+1是增函数”的条件是_____________,结论是________________.函数为y=2x+1该函数是增函数4.下列命题:
①面积相等的三角形是全等三角形;②若xy=0,则|x|+|y|=0;③若a>b,则ac2>bc2;④矩形的对角线互相垂直.
其中假命题的个数是________.1234解析 ①等底等高的三角形都是面积相等的三角形,但不一定全等;②当x,y中一个为零,另一个不为零时,|x|+|y|≠0;③当c=0时不成立;④菱形的对角线互相垂直,矩形的对角线不一定垂直.
答案 412341.根据命题的意义,可以判断真假的陈述句是命题,命题的条件与结论之间属于因果关系,真命题可以给出证明,假命题只需举出一个反例即可.
2.任何命题都是由条件和结论构成的,可以写成“若p,则q”的形式.含有大前提的命题写成“若p,则q”的形式,大前提应保持不变.呈重点、现规律归纳小结定义:陈述句、真假结构:若p,则q真假:p是否能推出q命题
人教版 选修2-1
1.1.1 命 题自主学习1.命题的定义是什么?在定义中有哪些关键字?2.命题是如何分类的?3.研究了命题的哪种结构形式?要点初探符号判断真假真假条件结论Contents Page明目标知重点填要点
记疑点探要点
究所然内容
索引010203当堂测
查疑缺 041.理解命题的概念和命题的构成,能判断给定陈述句是否为命题.
2.能判断命题的真假.
3.能把命题改写成“若p,则q”的形式.明目标、知重点1.命题的定义
用 表达的,可以判断 的_______
叫做命题.
判断为 的语句叫做 .
判断为 的语句叫做 .填要点·记疑点语言、符号或式子真假陈述句真假真命题假命题2.命题的结构
从构成来看,所有的命题都由 两部分构成.在数学中,命题常写成 这种形式,通常,我们把这种形式的命题中的p叫做 ,q叫做
.条件和结论“若p,则q”命题的条件命题的结论探要点·究所然情境导学我们在初中已经学过许多数学命题,但还不适应我们今后学习的需要,本节开始我们深化对命题的研究.思考1 在初中,我们已学过许多数学命题,当时是如何定义命题的,你能举出一个例子吗?
答 判断一件事情的句子.例如,有两边相等的三角形是等腰三角形.探究点一 命题的定义思考2 下面语句的表述形式有什么特点?
(1)若直线a∥b,则直线a和直线b无公共点;
(2)2+4=7;
(3)平面内垂直于同一条直线的两条直线平行;
(4)若x2=1,则x=1;
(5)两个全等三角形的面积相等;
(6)3能被2整除.
答 都是陈述句,都能判断真假.思考3 数学中的定义、公理、定理、推论是命题吗?
答 是.
小结 用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.例1 判断下面的语句是不是命题.
(1)空集是任何集合的子集.
(2)若整数a是素数,则a是奇数.
(3)指数函数是增函数吗?
(4)若平面上两条直线不相交,则这两条直线平行.
(6)x>15.
解 (1)(2)(4)(5)是命题.(3)(6)不是命题.反思与感悟 并不是所有的语句都是命题,只有能判断真假的陈述句才是命题,命题首先是“陈述句”,其他语句如疑问句、祈使句、感叹句等一般都不是命题;其次是“能判断真假”,不能判断真假的陈述句不是命题,如“x≥2”、“小高的个子很高”等都不能判断真假,故都不是命题.
因此,判断一个语句是否为命题,关键有两点:①是否为陈述句;②能否判断真假.跟踪训练1 判断下列语句是不是命题.
(1)求证 是无理数.
(2)x2+2x+1≥0.
(3)你是高二学生吗?
(4)并非所有的人都喜欢吃苹果.
(5)一个正整数不是质数就是合数.
(6)若x∈R,则x2+4x+7>0.
(7)x+3>0.
解 (1)(3)(7)不是命题,(2)(4)(5)(6)是命题.思考1 命题分哪几类?
答 真命题和假命题.
小结 判断为真的语句叫做真命题;判断为假的语句叫做假命题.探究点二 命题的分类例2 请对例1给出的命题判断真假.
解 (1)(4)(5)是真命题,(2)是假命题.反思与感悟 要判断一个命题是真命题,一般需要经过严格的推理论证,在判断时,要有理有据,有时应综合各种情况作出正确的判断,而判断一个命题是假命题,只需举出一个反例即可.跟踪训练2 判断下列命题的真假:
(1)已知a,b,c,d∈R,若a≠c,b≠d,则a+b≠c+d;
解 假命题.反例:1≠4,5≠2,而1+5=4+2.(2)若x∈N,则x3>x2成立;
解 假命题.反例:当x=0时,x3>x2不成立.(3)若m>1,则方程x2-2x+m=0无实数根;
解 真命题:∵m>1?Δ=4-4m<0,∴方程x2-2x+m=0无实数根.(4)存在一个三角形没有外接圆.
解 假命题.因为不共线的三点确定一个圆,即任何三角形都有外接圆.思考2 数学中的定义、公理、定理、推论是真命题吗?
答 是.思考1 跟踪训练2中(2)(3)两个命题是什么形式?命题的常见形式是什么?
答 命题(2)(3)具有“若p,则q”的形式,即为命题的常见形式.探究点三 命题的结构小结 命题由条件和结论两部分组成,它的结构形式为:“若p,则q”.也可写成:“如果p,那么q.其中p是命题的条件,q是命题的结论.思考2 指出下列命题中的条件p和结论q:
(1)若整数a能被2整除,则整数a是偶数;
答 条件p:整数a能被2整除,
结论q:整数a是偶数.(2)若四边形是菱形,则它的对角线互相垂直且平分.
答 条件p:四边形是菱形,
结论q:四边形的对角线互相垂直且平分.思考3 如何把命题改写成“若p,则q”的形式.
答 分清条件和结论.例3 将下列命题改写成“若p,则q”的形式,并判断真假.
(1)垂直于同一条直线的两条直线平行;
解 若两条直线垂直于同一条直线,则这两条直线平行.假命题.(2)负数的立方是负数;
解 若一个数是负数,则这一个数的立方是负数.真命题.(3)对顶角相等.
解 若两个角是对顶角,则这两个角相等.真命题.反思与感悟 把一个命题改写成“若p,则q”的形式,首先要确定命题的条件和结论,若条件和结论比较隐含,要补充完整,有时一个条件有多个结论,有时一个结论需多个条件,还要注意有的命题改写形式也不唯一.跟踪训练3 把下列命题改写成“若p,则q”的形式,并判断真假.
(1)实数的平方是非负数;
解 若一个数是实数,则它的平方是非负数.真命题.(2)等底等高的两个三角形是全等三角形;
解 若两个三角形等底等高,则这两个三角形是全等三角形.假命题.(3)当ac>bc时,a>b;
解 若ac>bc,则a>b.假命题.(4)角的平分线上的点到角的两边的距离相等.
解 若一个点是一个角的平分线上的点,则该点到这个角的两边的距离相等.真命题.当堂测·查疑缺 12341.下列语句是命题的是( )
A.2 014是一个大数
B.若两直线平行,则这两条直线没有公共点
C.对数函数是增函数吗
D.a≤15
解析 A、D不能判断真假,不是命题;B能够判断真假而且是陈述句,是命题;C是疑问句,不是命题.B2.下列命题中是真命题的是( )
A.互余的两个角不相等
B.相等的两个角是同位角
C.若a2=b2,则|a|=|b|
D.三角形的一个外角等于和它不相邻的一个内角
解析 由平面几何知识可知A、B、D三项都是错误的.1234C12343.命题“函数y=2x+1是增函数”的条件是_____________,结论是________________.函数为y=2x+1该函数是增函数4.下列命题:
①面积相等的三角形是全等三角形;②若xy=0,则|x|+|y|=0;③若a>b,则ac2>bc2;④矩形的对角线互相垂直.
其中假命题的个数是________.1234解析 ①等底等高的三角形都是面积相等的三角形,但不一定全等;②当x,y中一个为零,另一个不为零时,|x|+|y|≠0;③当c=0时不成立;④菱形的对角线互相垂直,矩形的对角线不一定垂直.
答案 412341.根据命题的意义,可以判断真假的陈述句是命题,命题的条件与结论之间属于因果关系,真命题可以给出证明,假命题只需举出一个反例即可.
2.任何命题都是由条件和结论构成的,可以写成“若p,则q”的形式.含有大前提的命题写成“若p,则q”的形式,大前提应保持不变.呈重点、现规律归纳小结定义:陈述句、真假结构:若p,则q真假:p是否能推出q命题
