《数系的扩充与复数的引入(复习参考题)》
文档属性
| 名称 | 《数系的扩充与复数的引入(复习参考题)》 |  | |
| 格式 | zip | ||
| 文件大小 | 765.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-20 21:11:02 | ||
图片预览








文档简介
课件26张PPT。21:03 数系的扩充与复数的引入(复习)
人教A版选修1-2第三章21:03 意大利米兰21:03 数学家卡尔丹思考?此方程在实数集中有解吗?数学家欧拉21:0321:03 虚数单位 i规定
新形式的数 2i,
3+2i, 3-2i
,4+0i,
21:03复数的代数表示形式 z = a + bi(a,b都是实数)
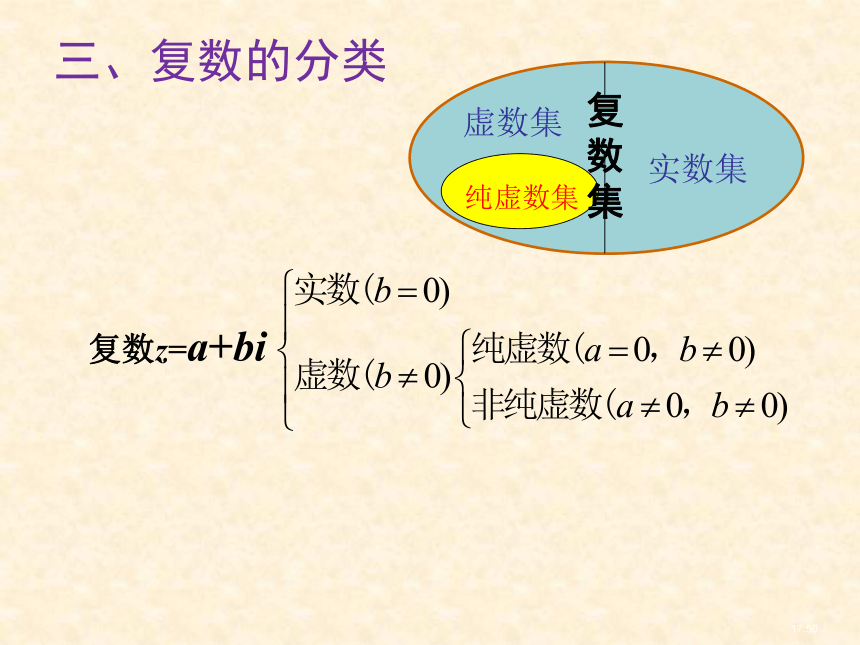
a —实部 b— 虚部21:03-复数z=a+bi21:03三、复数的分类自然数整数有理数实数?负整数分数无理数数 系 的 扩 充复数虚数21:0321:03, (21:03诊断性练习一1、说出下列复数的实部与虚部
2、指出下列各数哪些是实数?哪些是虚数?哪些又是纯虚数?
0
牛刀小试, , i ii,, , 21:03诊断性练习一3、判断对错
① 的实部是2,虚部是 ( )
②复数集就是虚数集( )
4、对于复数 ,它在复平面内对应点的坐标是( ),这个点在第( )象限,对应的向量 =( ),它的模 = ,
的共轭复数 ( )
, , i ii,, , 3 错错3,-4 四3,-4 53+4i21:035、复数 的积是实数的充要条件是( )
A、 B、
C、 D、
6、已知 ,则实数 ( )
( )
A1721:03例1 已知 是关于x的方程 的一个根,求实数 的值。
21:03例1 已知 是关于x的方程 的一个根,求实数 的值。
分析:利用方程根的定义及复数相等的充要条件。
解:由根的定义,将 代入方程,得到
整理得到
由复数相等的充要条件得 ,
解得
21:03例1 已知 是关于x的方程 的一个根,求实数 的值。
探究:你能否求出方程的另一个根,它与
是怎样的关系?
21:03复数的四则运算
巩固练习:计算
(1) (2)
(3) (4)21:03例2、已知 ,求 及
则
21:03于是
复数代数形式的四则运算应注意复数代数形式的加减法,形式上与多项式加减法类似;
复数乘法可按与多项式相乘类似的办法进行,而不必记忆公式,注意 ;
复数的除法大家可以类比根式的除法,先把两个复数相除写成分数形式,然后把分子分母都乘以分母的共轭复数,使分母“实数化”,最后化简。
21:0321:031、已知i为虚数, ,若关于x的方程
有实根,则m的取值为( )(讨论探究)
A、 B、 C、 D、
其中,,,,
21:0321:0321:031、已知i为虚数, ,若关于x的方程
有实根,则m的取值为( )(讨论探究)
A、 B、 C、 D、
2、(2017年课标全国Ⅰ)设有下面四个命题:
P1:若复数z满足 ,则
P2:若复数z满足 ,则
P3:若复数 ,满足 、则
P4:若复数 ,则 其中的真命题是( )z 其中
其中,,,,
21:03 虚数是奇妙的人类精神的寄托,
它好像是存在与不存在之间的一种两栖动物。
——莱布尼兹
人教A版选修1-2第三章21:03 意大利米兰21:03 数学家卡尔丹思考?此方程在实数集中有解吗?数学家欧拉21:0321:03 虚数单位 i规定
新形式的数 2i,
3+2i, 3-2i
,4+0i,
21:03复数的代数表示形式 z = a + bi(a,b都是实数)
a —实部 b— 虚部21:03-复数z=a+bi21:03三、复数的分类自然数整数有理数实数?负整数分数无理数数 系 的 扩 充复数虚数21:0321:03, (21:03诊断性练习一1、说出下列复数的实部与虚部
2、指出下列各数哪些是实数?哪些是虚数?哪些又是纯虚数?
0
牛刀小试, , i ii,, , 21:03诊断性练习一3、判断对错
① 的实部是2,虚部是 ( )
②复数集就是虚数集( )
4、对于复数 ,它在复平面内对应点的坐标是( ),这个点在第( )象限,对应的向量 =( ),它的模 = ,
的共轭复数 ( )
, , i ii,, , 3 错错3,-4 四3,-4 53+4i21:035、复数 的积是实数的充要条件是( )
A、 B、
C、 D、
6、已知 ,则实数 ( )
( )
A1721:03例1 已知 是关于x的方程 的一个根,求实数 的值。
21:03例1 已知 是关于x的方程 的一个根,求实数 的值。
分析:利用方程根的定义及复数相等的充要条件。
解:由根的定义,将 代入方程,得到
整理得到
由复数相等的充要条件得 ,
解得
21:03例1 已知 是关于x的方程 的一个根,求实数 的值。
探究:你能否求出方程的另一个根,它与
是怎样的关系?
21:03复数的四则运算
巩固练习:计算
(1) (2)
(3) (4)21:03例2、已知 ,求 及
则
21:03于是
复数代数形式的四则运算应注意复数代数形式的加减法,形式上与多项式加减法类似;
复数乘法可按与多项式相乘类似的办法进行,而不必记忆公式,注意 ;
复数的除法大家可以类比根式的除法,先把两个复数相除写成分数形式,然后把分子分母都乘以分母的共轭复数,使分母“实数化”,最后化简。
21:0321:031、已知i为虚数, ,若关于x的方程
有实根,则m的取值为( )(讨论探究)
A、 B、 C、 D、
其中,,,,
21:0321:0321:031、已知i为虚数, ,若关于x的方程
有实根,则m的取值为( )(讨论探究)
A、 B、 C、 D、
2、(2017年课标全国Ⅰ)设有下面四个命题:
P1:若复数z满足 ,则
P2:若复数z满足 ,则
P3:若复数 ,满足 、则
P4:若复数 ,则 其中的真命题是( )z 其中
其中,,,,
21:03 虚数是奇妙的人类精神的寄托,
它好像是存在与不存在之间的一种两栖动物。
——莱布尼兹
