2.2.2 反证法
图片预览










文档简介
课件36张PPT。人教A版选修1-2第二章推理与证明
2.2.2间接证明
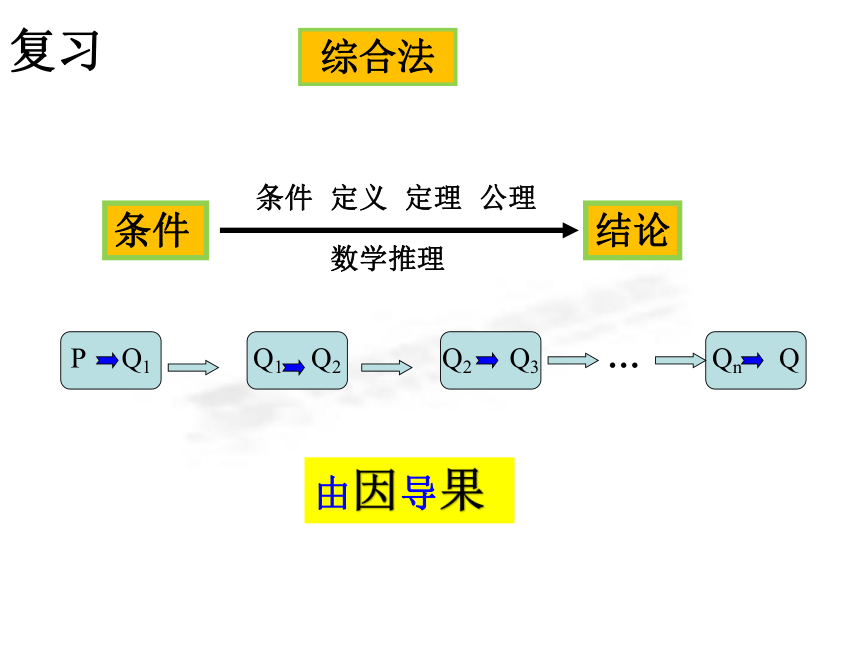
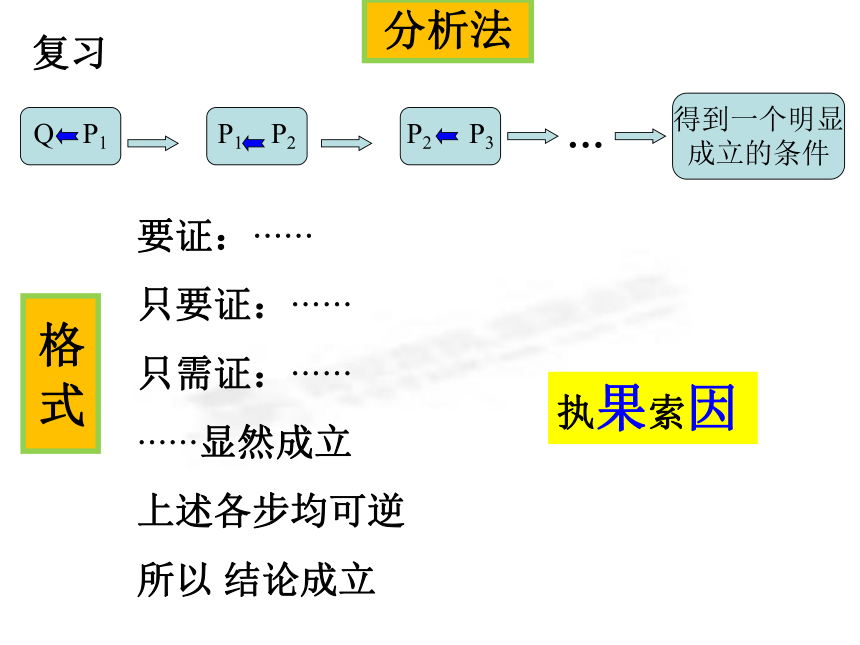
---反证法综合法由因导果复习分析法要证:??
只要证:??
只需证:??
??显然成立
上述各步均可逆
所以 结论成立格 式复习执果索因1.直接证明的方法:(1)比较法:作差比较法;作商比较法;(2)综合法:(3)分析法:2.没有特别要求的证明题:
用分析法寻找证明思路,用综合法写出证明过程!1.了解反证法是间接证明的一种基本方法;
2.识别反证法所适用的数学问题;
3.理解反证法的思考过程(反设,归谬);4.会用反证法解决数学问题.2.2.2 反证法学习目标:思考: 将9个球分别染成红色或白色,那么无论怎样染,至少有5个球是同色的。你能证明这个结论吗?1.间接证明(基本概念)间接证明是不同于直接证明的又一类
证明方法.反证法是一种常用的间接证明方法.新课讲解2.
假设原命题 (即在原命题的条件下,结论不成立),经过
正确的推理,最后得出矛盾,因此说明________ ,
从而证明了 ,这样的证明方法叫做反证法.
3.反证法常见的矛盾类型
反证法的关键是在正确的推理下得出矛盾.这个矛盾可以是与
矛盾,或与假设矛盾,或与
矛盾等.不成 立假设错误原命题成立已知条件定义、公理、定理、事实5.反证法的思维方法:正难则反反证法定义:一、提出假设二、推理论证三、得出矛盾四、结论成立6.反证法的一般步骤类型一 用反证法证明否定性命题例1:设{an}是公比为q的等比数列.设q≠1,
证明:数列{an+1}不是等比数列.7.反证法所适用的证明问题 用反证法证明否定性命题的适用类型:
结论中含有“不”“不是”“不可能”“不存在”等词语的命题称为否定性命题,此类问题的正面比较模糊,而反面比较具体,适合使用反证法.
4.已知 ,
求证:方程 没有负数根2. 求证: 不可能是同一个等差
数列中的三项.3.已知0(1-c)a, 不能都大于1/4类型二 用反证法证明“至多、至少”类问题1.已知a,b,c是互不相等的实数,求证:
由y1=ax2+2bx+c,
y2=bx2+2cx+a和
y3=cx2+2ax+b确定的三条抛物线
至少有一条与x轴有两个不同的交点.2.若函数f(x)在区间[a,b]上是增函数,
求证:方程f(x)=0在区间[a,b]上至多有一个
实根. 3.用反证法证明:关于x的方程x2+4ax-4a
+3=0,x2+(a-1)x+a2=0,x2+2ax-
2a=0,当a≤- 或a≥-1时,
至少有一个方程有实数根.类型三 用反证法证明唯一性命题例3 求证:方程2x=3有且只有一个根.用反证法证明唯一性命题的类型:以“有且只有”,“只有一个”,“唯一存在”等形式出现的命题。宜用反证法证明的题型 (1)以否定性判断作为结论的命题.(2)某些定理的逆命题.(3)以“至多”、“至少”或“不多于”等形式陈
述的命题.(4)关于“唯一性”结论的命题.(8)涉及各种“无限”结论的命题等.(7)有些基本定理或某一知识体系的初始阶段.(6)一些不等量命题的证明.(5)解决整除性问题. 准确地作出反设(即否定结论)是非常重要的,下面是一些常见的结论的否定形式. ?不是不都是不大于大于或等于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某x,
不成立存在某x,
成立不等于某个¬p且¬q¬p或¬q1.写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于ba不平行b练习2. 用反证法证明命题“三角形中最多有一个是直角”
时,应假设 ____________ .三角形中有两个或三个角是直角3.否定“自然数a,b,c中恰有一个偶数”时,正
确的反设为( )
A.a,b,c都是奇数
B. a,b,c都是偶数
C. a,b,c中至少有两个偶数
D. a,b,c中都是奇数或至少有两个偶数D4.用反证法证明(填空):
在三角形的内角中,至少有一个角不小于60°已知:如图, ∠A,∠B,∠C是△ABC的内角求证: ∠A,∠B,∠C中至少有一个角不小于600.证明:假设所求证的结论不成立,即
∠A__60°, ∠B__60°, ∠C__60°
则 ∠A+∠B+∠C < 1800
这于_______________矛盾
所以假设______,
所以,所求证的结论成立.<<<三角形三个内角的和等于180°不成立5.求证:在同一平面内,如果一条直线和两条平
行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.l1l2l3Pl3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线与已知直线平行假设推理矛盾假设不成立命题成立1例1、已知a≠0,证明:关于x的方程
ax=b有且只有一个根.分析:由于a≠0,因此方程至少有一个根x= 。从正面较难说清为什么只有这个根,我们采用反证法,即证明如果不只一个根则会导致矛盾。1例1:已知a≠0,证明:关于x的方程ax=b有且只有一个根。练习:课本43页练习用反证法证题时,应注意的事项 :
??(1)周密考察原命题结论的否定事项,
防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说
明命题的真伪性;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
11、知识小结:
反证法证明的思路:假设命题的结论不成立→正确的推理,得出矛盾→否定假设,肯定待证明的命题2、重、难点提示:
反设是反证法的基础;归谬是反证法的关键,导出矛盾的过程没有固定的模式。例3.已知:求证:(2)中至少有一个不小于. (1)作业: 课本44页 习题2.2A组第3题 再见
2.2.2间接证明
---反证法综合法由因导果复习分析法要证:??
只要证:??
只需证:??
??显然成立
上述各步均可逆
所以 结论成立格 式复习执果索因1.直接证明的方法:(1)比较法:作差比较法;作商比较法;(2)综合法:(3)分析法:2.没有特别要求的证明题:
用分析法寻找证明思路,用综合法写出证明过程!1.了解反证法是间接证明的一种基本方法;
2.识别反证法所适用的数学问题;
3.理解反证法的思考过程(反设,归谬);4.会用反证法解决数学问题.2.2.2 反证法学习目标:思考: 将9个球分别染成红色或白色,那么无论怎样染,至少有5个球是同色的。你能证明这个结论吗?1.间接证明(基本概念)间接证明是不同于直接证明的又一类
证明方法.反证法是一种常用的间接证明方法.新课讲解2.
假设原命题 (即在原命题的条件下,结论不成立),经过
正确的推理,最后得出矛盾,因此说明________ ,
从而证明了 ,这样的证明方法叫做反证法.
3.反证法常见的矛盾类型
反证法的关键是在正确的推理下得出矛盾.这个矛盾可以是与
矛盾,或与假设矛盾,或与
矛盾等.不成 立假设错误原命题成立已知条件定义、公理、定理、事实5.反证法的思维方法:正难则反反证法定义:一、提出假设二、推理论证三、得出矛盾四、结论成立6.反证法的一般步骤类型一 用反证法证明否定性命题例1:设{an}是公比为q的等比数列.设q≠1,
证明:数列{an+1}不是等比数列.7.反证法所适用的证明问题 用反证法证明否定性命题的适用类型:
结论中含有“不”“不是”“不可能”“不存在”等词语的命题称为否定性命题,此类问题的正面比较模糊,而反面比较具体,适合使用反证法.
4.已知 ,
求证:方程 没有负数根2. 求证: 不可能是同一个等差
数列中的三项.3.已知0
由y1=ax2+2bx+c,
y2=bx2+2cx+a和
y3=cx2+2ax+b确定的三条抛物线
至少有一条与x轴有两个不同的交点.2.若函数f(x)在区间[a,b]上是增函数,
求证:方程f(x)=0在区间[a,b]上至多有一个
实根. 3.用反证法证明:关于x的方程x2+4ax-4a
+3=0,x2+(a-1)x+a2=0,x2+2ax-
2a=0,当a≤- 或a≥-1时,
至少有一个方程有实数根.类型三 用反证法证明唯一性命题例3 求证:方程2x=3有且只有一个根.用反证法证明唯一性命题的类型:以“有且只有”,“只有一个”,“唯一存在”等形式出现的命题。宜用反证法证明的题型 (1)以否定性判断作为结论的命题.(2)某些定理的逆命题.(3)以“至多”、“至少”或“不多于”等形式陈
述的命题.(4)关于“唯一性”结论的命题.(8)涉及各种“无限”结论的命题等.(7)有些基本定理或某一知识体系的初始阶段.(6)一些不等量命题的证明.(5)解决整除性问题. 准确地作出反设(即否定结论)是非常重要的,下面是一些常见的结论的否定形式. ?不是不都是不大于大于或等于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某x,
不成立存在某x,
成立不等于某个¬p且¬q¬p或¬q1.写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于ba不平行b练习2. 用反证法证明命题“三角形中最多有一个是直角”
时,应假设 ____________ .三角形中有两个或三个角是直角3.否定“自然数a,b,c中恰有一个偶数”时,正
确的反设为( )
A.a,b,c都是奇数
B. a,b,c都是偶数
C. a,b,c中至少有两个偶数
D. a,b,c中都是奇数或至少有两个偶数D4.用反证法证明(填空):
在三角形的内角中,至少有一个角不小于60°已知:如图, ∠A,∠B,∠C是△ABC的内角求证: ∠A,∠B,∠C中至少有一个角不小于600.证明:假设所求证的结论不成立,即
∠A__60°, ∠B__60°, ∠C__60°
则 ∠A+∠B+∠C < 1800
这于_______________矛盾
所以假设______,
所以,所求证的结论成立.<<<三角形三个内角的和等于180°不成立5.求证:在同一平面内,如果一条直线和两条平
行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.l1l2l3Pl3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线与已知直线平行假设推理矛盾假设不成立命题成立1例1、已知a≠0,证明:关于x的方程
ax=b有且只有一个根.分析:由于a≠0,因此方程至少有一个根x= 。从正面较难说清为什么只有这个根,我们采用反证法,即证明如果不只一个根则会导致矛盾。1例1:已知a≠0,证明:关于x的方程ax=b有且只有一个根。练习:课本43页练习用反证法证题时,应注意的事项 :
??(1)周密考察原命题结论的否定事项,
防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说
明命题的真伪性;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
11、知识小结:
反证法证明的思路:假设命题的结论不成立→正确的推理,得出矛盾→否定假设,肯定待证明的命题2、重、难点提示:
反设是反证法的基础;归谬是反证法的关键,导出矛盾的过程没有固定的模式。例3.已知:求证:(2)中至少有一个不小于. (1)作业: 课本44页 习题2.2A组第3题 再见
