高一数学(必修3)期中期末备考精讲精练专题04+统计(精练)
文档属性
| 名称 | 高一数学(必修3)期中期末备考精讲精练专题04+统计(精练) |

|
|
| 格式 | zip | ||
| 文件大小 | 244.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-20 00:00:00 | ||
图片预览



文档简介
一、选择题
1.某学校为了调查高一年级的200名学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机抽取20名同学进行抽查;第二种由教务处对该年级的学生进行编号,从001到200,抽取学号最后一位为2的同学进行调查.则这两种抽样的方法依次是( )
A.分层抽样,简单随机抽样 B.简单随机抽样,分层抽样
C.分层抽样,系统抽样 D.简单随机抽样,系统抽样
【答案】D
【解析】由抽样方法的概念知,第一种是简单随机抽样,第二种是系统抽样.
2.小波一星期的总开支分布如图①所示,一星期的食品开支如图②所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
A.1% B.2%
C.3% D.5%
【答案】C
【解析】由题图②知,小波一星期的食品开支为300元,其中鸡蛋开支为30元,占食品开支的10%,而食品开支占总开支的30%,所以小波一星期的鸡蛋开支占总开支的百分比为3%.
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数与实际平均数的差是( )
A.3.5 B.-3
C.3 D.-0.5
【答案】B
4.某校现有高一学生210人,高二学生270人,高三学生300人,学校学生会用分层抽样的方法从这三个年级的学生中抽取n个学生进行问卷调查,如果已知从高一学生中抽取的人数为7人,那么从高三学生中抽取的人数应为( )
A.10 B.9
C.8 D.7
【答案】A
【解析】由题意知抽取的比例为=,故从高三中抽取的人数为300×=10.
5.一个容量为100的样本,其数据的分组与各组的频数如下:
组别
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
12
13
24
15
16
13
7
则样本数据在[10,40)上的频率为( )
A.0.13 B.0.39
C.0.52 D.0.64
【答案】C
【解析】频率为=0.52.
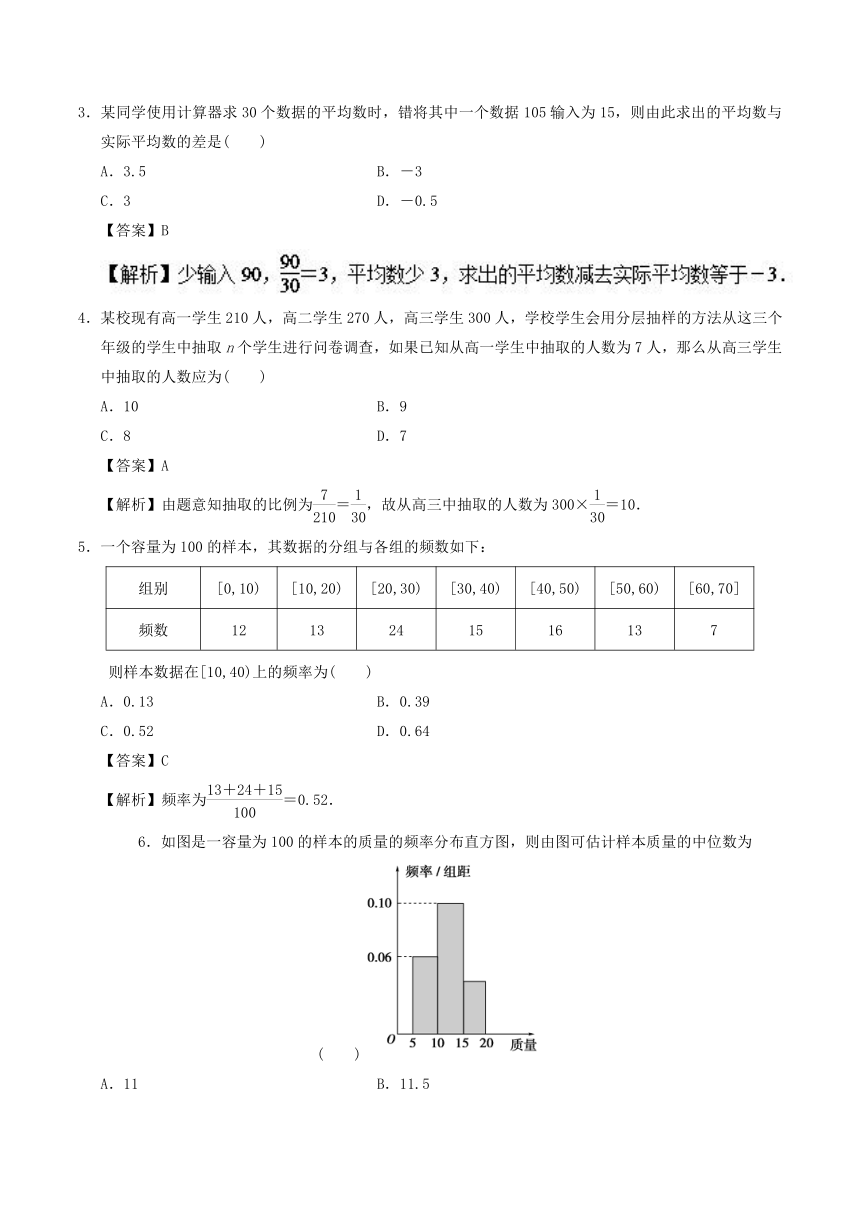
6.如图是一容量为100的样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( )
A.11 B.11.5
C.12 D.12.5
【答案】C
【解析】由频率分布直方图得组距为5,故样本质量在[5,10),[10,15)内的频率分别为0.3和0.5,从而中位数为10+×5=12,故选C.
7.高三某班有学生56人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、33号、47号学生在样本中,则样本中还有一个学生的编号为( )
A.13 B.17
C.19 D.21
【答案】C
【解析】因为47-33=14,所以由系统抽样的定义可知样本中的另一个学生的编号为5+14=19.
8.在某次测量中得到的A样本数据如下:52,54,54,56,56,56,55,55,55,55.若B样本数据恰好是A样本数据都加6后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.众数 B.平均数
C.中位数 D.标准差
【答案】D
二、填空题
9.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查,已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6,则应从一年级本科生中抽取________名学生.
【答案】60
【解析】根据题意,应从一年级本科生中抽取的人数为×300=60.
10.某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测试分析,得到如图所示的时速的频率分布直方图,根据下图,时速在70 km/h以下的汽车有________辆.
【答案】20【解析】由频率分布直方图可得时速在70 km/h以下的频率是(0.01+0.03)×10=0.4,所以频数是0.4×50=20.三、解答题
11.某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数
1
1
1
2
2
1
2
用水量/吨
22
38
40
41
44
50
95
(1)在这10天中,该公司用水量的平均数是多少?
(2)在这10天中,该公司每天用水量的中位数是多少?
(3)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
【解析】(1)=(22+38+40+2×41+2×44+50+2×95)=51(吨).
(2)中位数为=42.5(吨).
(3)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下,故用中位数描述每天的用水量更合适.
12.农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在如图给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
【解析】(1)茎叶图如图所示:
(2)甲==12,乙==13,
s≈13.67,s≈16.67.
因为甲<乙,所以乙种麦苗平均株高较高,又因为s<s,所以甲种麦苗长得较为整齐.
一、选择题
1.如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩.(单位:分)
已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )
A.2,6 B.2,7
C.3,6 D.5,7
【答案】D
【解析】依题意得9+10×2+2+x+20×2+7+4=17×5,即x=5,y=7,故选D.
2.在样本频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的,且样本容量为160,则中间一组的频数为( )
A.32 B.0.2
C.40 D.0.25
【答案】A
【解析】由频率分布直方图的性质,可设中间一组的频率为x,则x+4x=1,
所以x=0.2,故中间一组的频数为160×0.2=32,选A.
3.如图所示,样本A和B分别取自两个不同的总体,它们的样本平均数分别为A和B,样本标准差分别为sA和sB,则( )
A.A>B,sA>sB B.A<B,sA>sB
C.A>B,sA<sB D.A<B,sA<sB
【答案】B
4.某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A.,s2+1002 B.+100,s2+1002
C.,s2 D.+100,s2
【答案】D
【解析】=,yi=xi+100,所以y1,y2,…,y10的均值为+100,方差不变,故选D.
二、填空题
5.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
零件数x(个)
10
20
30
40
50
加工时间y(分钟)
64
69
75
82
90
由表中数据,求得线性回归方程为=0.65x+,根据回归方程,预测加工70个零件所花费的时间为________分钟.
【答案】102
【解析】由数据可得=30,=76,将中心点(30,76)代入线性回归方程可得=76-0.65×30=56.5,所以线性回归方程为=0.65x+56.5.当x=70时,=0.65×70+56.5=102.
6.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]的学生中选取的人数应为________.
【答案】0.030 3
三、解答题
7.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程=bx+a;
(3)试预测加工10个零件需要多少小时?
(注:b=,a=-b )
【解析】(1)散点图如图.
(2)由表中数据得xiyi=52.5,=3.5,=3.5,x=54.
∴b=0.7,∴a=1.05.∴=0.7x+1.05.
(3)将x=10代入回归直线方程,得=0.7×10+1.05=8.05(小时).
∴预测加工10个零件需要8.05小时.
8.某班100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段
[50,60)
[60,70)
[70,80)
[80,90)
x∶y
1∶1
2∶1
3∶4
4∶5
【解析】(1)由频率分布直方图知(2a+0.02+0.03+0.04)×10=1,解得a=0.005.
(2)由频率分布直方图知这100名学生语文成绩的平均分为55×0.005×10+65×0.04×10+75×0.03×10+85×0.02×10+95×0.005×10=73(分).
(3)由频率分布直方图知语文成绩在[50,60),[60,70),[70,80),[80,90)各分数段的人数依次为0.005×10×100=5;0.04×10×100=40;0.03×10×100=30;0.02×10×100=20.
由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5;40×=20;30×=40;20×=25.
故数学成绩在[50,90)之外的人数为100-(5+20+40+25)=10.
同课章节目录
