2018年八年级数学上册第十一章三角形11.2与三角形有关的角11.2.1三角形内角和定理习题(含答案)
文档属性
| 名称 | 2018年八年级数学上册第十一章三角形11.2与三角形有关的角11.2.1三角形内角和定理习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 83.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-21 00:00:00 | ||
图片预览


文档简介
11.2.1 三角形内角和定理
学校:___________姓名:___________班级:___________
一.选择题(共10小题)
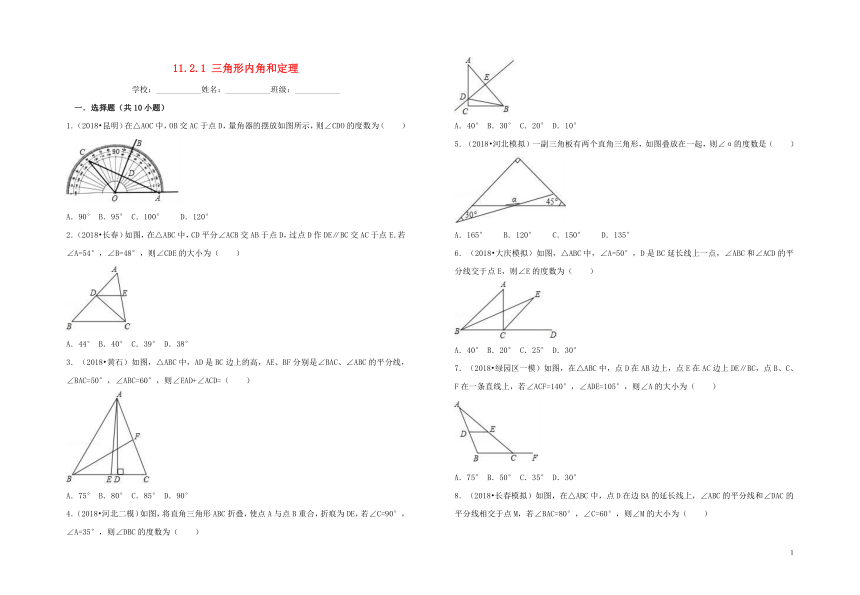
1.(2018?昆明)在△AOC中,OB交AC于点D,量角器的摆放如图所示,则∠CDO的度数为( )
A.90° B.95° C.100° D.120°
2.(2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°
3.(2018?黄石)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
4.(2018?河北二模)如图,将直角三角形ABC折叠,使点A与点B重合,折痕为DE,若∠C=90°,∠A=35°,则∠DBC的度数为( )
A.40° B.30° C.20° D.10°
5.(2018?河北模拟)一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
6.(2018?大庆模拟)如图,△ABC中,∠A=50°,D是BC延长线上一点,∠ABC和∠ACD的平分线交于点E,则∠E的度数为( )
A.40° B.20° C.25° D.30°
7.(2018?绿园区一模)如图,在△ABC中,点D在AB边上,点E在AC边上DE∥BC,点B、C、F在一条直线上,若∠ACF=140°,∠ADE=105°,则∠A的大小为( )
A.75° B.50° C.35° D.30°
8.(2018?长春模拟)如图,在△ABC中,点D在边BA的延长线上,∠ABC的平分线和∠DAC的平分线相交于点M,若∠BAC=80°,∠C=60°,则∠M的大小为( )
A.20° B.25° C.30° D.35°
9.(2018?裕华区一模)如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
10.(2018?津南区二模)如图,△ABC纸片中,∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD、则∠EDB的度数为( )
A.76° B.74° C.72° D.70°
二.填空题(共8小题)
11.(2018?永州)一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC= .
12.(2018?滨州)在△ABC中,若∠A=30°,∠B=50°,则∠C= .
13.(2018?微山县一模)如图,点E在△ABC边BC的延长线上,CD平分∠ACE,若∠A=70°,∠DCA=65°,则∠B的度数是 .
14.(2018?兴化市一模)如果将一副三角板按如图方式叠放,那么∠1= .
15.(2018?南开区模拟)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,则∠A1= .∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2009BC的平分线与∠A2009CD的平分线交于点A2010,得∠A2010,则∠A2010= .
16.(2018?岐山县三模)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,∠DAE 度.
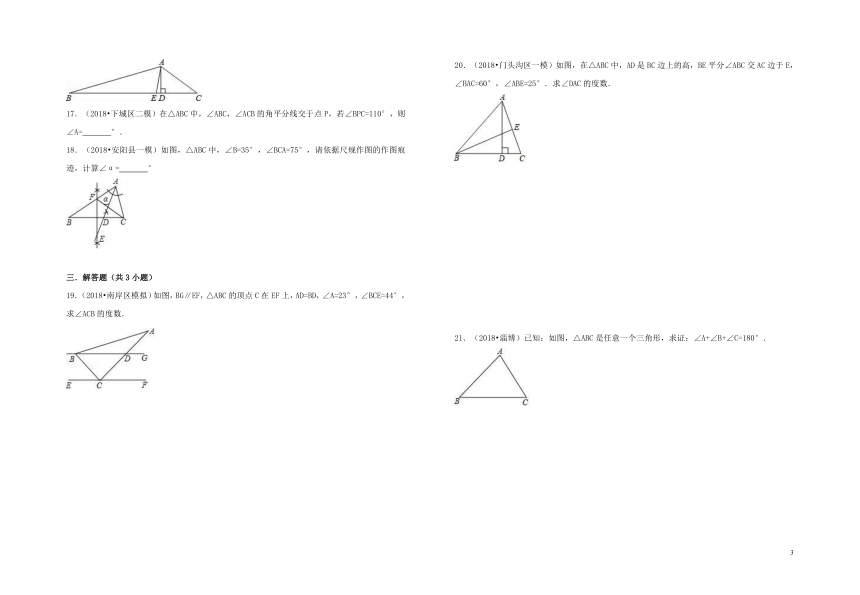
17.(2018?下城区二模)在△ABC中,∠ABC,∠ACB的角平分线交于点P,若∠BPC=110°,则∠A= °.
18.(2018?安阳县一模)如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α= °
三.解答题(共3小题)
19.(2018?南岸区模拟)如图,BG∥EF,△ABC的顶点C在EF上,AD=BD,∠A=23°,∠BCE=44°,求∠ACB的度数.
20.(2018?门头沟区一模)如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°.求∠DAC的度数.
21.(2018?淄博)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
参考答案与试题解析
一.选择题(共10小题)
1.解:∵CO=AO,∠AOC=130°,
∴∠CAO=25°,
又∵∠AOB=70°,
∴∠CDO=∠CAO+∠AOB=25°+70°=95°,
故选:B.
2.解:∵∠A=54°,∠B=48°,
∴∠ACB=180°﹣54°﹣48°=78°,
∵CD平分∠ACB交AB于点D,
∴∠DCB=78°=39°,
∵DE∥BC,
∴∠CDE=∠DCB=39°,
故选:C.
3.解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
4.解:∵∠C=90°,∠A=35°,
∴∠ABC=55°,
由折叠可得,∠A=∠ABD=35°,
∴∠DBC=∠ABC﹣∠ABD=55°﹣35°=20°.
故选:C.
5.解:给图中标上∠1、∠2,如图所示.
∵∠1+45°+90°=180°,
∴∠1=45°,
∵∠1=∠2+30°,
∴∠2=15°.
又∵∠2+∠α=180°,
∴∠α=165°.
故选:A.
6.
解:∵由三角形的外角的性质可知,∠E=∠ECD﹣∠EBD,
∵∠ABC的平分线与∠ACD的平分线交于点E,
∴∠EBC=∠ABC,∠ECD=∠ACD,
∵∠ACD﹣∠ABC=∠A=50°,
∴(∠ACD﹣∠ABC)=25°,
∴∠E=∠ECD﹣∠EBD=25°,
故选:C.
7.解:∵DE∥BC,
∴∠DEC=∠ACF=140°,
∴∠AED=180°﹣140°=40°,
∵∠ADE=105°,
∴∠A=180°﹣105°﹣40°=35°,
故选:C.
8.解:∵∠BAC=80°,∠C=60°,
∴∠ABC=40°,
∵∠ABC的平分线和∠DAC的平分线相交于点M,
∴∠ABM=20°,∠CAM=,
∴∠M=180°﹣20°﹣50°﹣80°=30°,
故选:C.
9.解:∵将△ABC沿DE,EF翻折,
∴∠A=∠DOE,∠B=∠FOE,
∴∠DOF=∠DOE+∠EOF=∠A+∠B=142°,
∴∠C=180°﹣∠A﹣∠B=180°﹣142°=38°,
故选:A.
10.解:∵∠A=56°,∠C=88°,
∴∠ABC=180°﹣56°﹣88°=36°,
∵沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,
∴∠CBD=∠DBE=18°,∠C=∠DEB=84°,
∴∠EDB=180°﹣18°﹣88°=74°.
故选:B.
二.填空题(共8小题)
11.解:∵∠CEA=60°,∠BAE=45°,
∴∠ADE=180°﹣∠CEA﹣∠BAE=75°,
∴∠BDC=∠ADE=75°,
故答案为75°.
12.解:∵在△ABC中,∠A=30°,∠B=50°,
∴∠C=180°﹣30°﹣50°=100°.
故答案为:100°
13.解:∵CD平分∠ACE,∠DCA=65°,
∴∠ACE=2∠DCA=130°,
又∵∠A=70°,
∴∠B=130°﹣70°=60°,
故答案为:60°.
14.解:给图中角标上序号,如图所示.
∵∠2+∠3+45°=180°,∠2=30°,
∴∠3=180°﹣30°﹣45°=105°,
∴∠1=∠3=105°.
故答案为:105°.
15.
解:∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∠ACD=2∠A1CD,∠ABC=2∠A1BC,
∴2∠A1CD=∠A+2∠A1BC,即∠A1CD=∠A+∠A1BC,
∴∠A1==,
由此可得∠A2010=.
故答案为:,.
16.解:∵AE是△ABC的角平分线,
∴∠CAE=∠BAC=×128°=64°,
∵AD⊥BC,
∴∠CAD=90°﹣∠C=90°﹣36°=54°,
∴∠DAE=∠CAE﹣∠CAD=64°﹣54°=10°.
故答案为:10.
17.解:如图所示:
∵∠ABC,∠ACB的角平分线交于点P,
∴∠ABP=∠PBC,∠ACP=∠PCB,
∵∠BPC=110°,
∴∠PBC+∠PCB=70°,
∴∠ABC+∠ACB=140°,
∴∠A=180°﹣140°=40°.
故答案为:40.
18.解:∵∠B=35°,∠BCA=75°,
∴∠BAC=70°,
∵由作法可知,AD是∠BAC的平分线,
∴∠CAD=∠BAC=35°,
∵由作法可知,EF是线段BC的垂直平分线,
∴∠BCF=∠B=35°,
∵∠ACF=∠ACB﹣∠BCF=40°,
∴∠α=∠CAD+∠ACF=75°,
故答案为:75.
三.解答题(共3小题)
19.解:∵AD=BD,∠A=23°,
∴∠ABD=∠A=23°,
∵BG∥EF,∠BCE=44°,
∴∠DBC=∠BCE=44°,
∴∠ABC=44°+23°=67°,
∴∠ACB=180°﹣67°﹣23°=90°.
20.解:∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∵AD是BC边上的高,
∴∠BAD=90°﹣∠ABC=90°﹣50°=40°,
∴∠DAC=∠BAC﹣∠BAD=60°﹣40°=20°.
21.证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°,
即∠A+∠B+∠C=180°.
学校:___________姓名:___________班级:___________
一.选择题(共10小题)
1.(2018?昆明)在△AOC中,OB交AC于点D,量角器的摆放如图所示,则∠CDO的度数为( )
A.90° B.95° C.100° D.120°
2.(2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44° B.40° C.39° D.38°
3.(2018?黄石)如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
4.(2018?河北二模)如图,将直角三角形ABC折叠,使点A与点B重合,折痕为DE,若∠C=90°,∠A=35°,则∠DBC的度数为( )
A.40° B.30° C.20° D.10°
5.(2018?河北模拟)一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
6.(2018?大庆模拟)如图,△ABC中,∠A=50°,D是BC延长线上一点,∠ABC和∠ACD的平分线交于点E,则∠E的度数为( )
A.40° B.20° C.25° D.30°
7.(2018?绿园区一模)如图,在△ABC中,点D在AB边上,点E在AC边上DE∥BC,点B、C、F在一条直线上,若∠ACF=140°,∠ADE=105°,则∠A的大小为( )
A.75° B.50° C.35° D.30°
8.(2018?长春模拟)如图,在△ABC中,点D在边BA的延长线上,∠ABC的平分线和∠DAC的平分线相交于点M,若∠BAC=80°,∠C=60°,则∠M的大小为( )
A.20° B.25° C.30° D.35°
9.(2018?裕华区一模)如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠DOF=142°,则∠C的度数为( )
A.38° B.39° C.42° D.48°
10.(2018?津南区二模)如图,△ABC纸片中,∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD、则∠EDB的度数为( )
A.76° B.74° C.72° D.70°
二.填空题(共8小题)
11.(2018?永州)一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC= .
12.(2018?滨州)在△ABC中,若∠A=30°,∠B=50°,则∠C= .
13.(2018?微山县一模)如图,点E在△ABC边BC的延长线上,CD平分∠ACE,若∠A=70°,∠DCA=65°,则∠B的度数是 .
14.(2018?兴化市一模)如果将一副三角板按如图方式叠放,那么∠1= .
15.(2018?南开区模拟)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,则∠A1= .∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2009BC的平分线与∠A2009CD的平分线交于点A2010,得∠A2010,则∠A2010= .
16.(2018?岐山县三模)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,∠DAE 度.
17.(2018?下城区二模)在△ABC中,∠ABC,∠ACB的角平分线交于点P,若∠BPC=110°,则∠A= °.
18.(2018?安阳县一模)如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α= °
三.解答题(共3小题)
19.(2018?南岸区模拟)如图,BG∥EF,△ABC的顶点C在EF上,AD=BD,∠A=23°,∠BCE=44°,求∠ACB的度数.
20.(2018?门头沟区一模)如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°.求∠DAC的度数.
21.(2018?淄博)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
参考答案与试题解析
一.选择题(共10小题)
1.解:∵CO=AO,∠AOC=130°,
∴∠CAO=25°,
又∵∠AOB=70°,
∴∠CDO=∠CAO+∠AOB=25°+70°=95°,
故选:B.
2.解:∵∠A=54°,∠B=48°,
∴∠ACB=180°﹣54°﹣48°=78°,
∵CD平分∠ACB交AB于点D,
∴∠DCB=78°=39°,
∵DE∥BC,
∴∠CDE=∠DCB=39°,
故选:C.
3.解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
4.解:∵∠C=90°,∠A=35°,
∴∠ABC=55°,
由折叠可得,∠A=∠ABD=35°,
∴∠DBC=∠ABC﹣∠ABD=55°﹣35°=20°.
故选:C.
5.解:给图中标上∠1、∠2,如图所示.
∵∠1+45°+90°=180°,
∴∠1=45°,
∵∠1=∠2+30°,
∴∠2=15°.
又∵∠2+∠α=180°,
∴∠α=165°.
故选:A.
6.
解:∵由三角形的外角的性质可知,∠E=∠ECD﹣∠EBD,
∵∠ABC的平分线与∠ACD的平分线交于点E,
∴∠EBC=∠ABC,∠ECD=∠ACD,
∵∠ACD﹣∠ABC=∠A=50°,
∴(∠ACD﹣∠ABC)=25°,
∴∠E=∠ECD﹣∠EBD=25°,
故选:C.
7.解:∵DE∥BC,
∴∠DEC=∠ACF=140°,
∴∠AED=180°﹣140°=40°,
∵∠ADE=105°,
∴∠A=180°﹣105°﹣40°=35°,
故选:C.
8.解:∵∠BAC=80°,∠C=60°,
∴∠ABC=40°,
∵∠ABC的平分线和∠DAC的平分线相交于点M,
∴∠ABM=20°,∠CAM=,
∴∠M=180°﹣20°﹣50°﹣80°=30°,
故选:C.
9.解:∵将△ABC沿DE,EF翻折,
∴∠A=∠DOE,∠B=∠FOE,
∴∠DOF=∠DOE+∠EOF=∠A+∠B=142°,
∴∠C=180°﹣∠A﹣∠B=180°﹣142°=38°,
故选:A.
10.解:∵∠A=56°,∠C=88°,
∴∠ABC=180°﹣56°﹣88°=36°,
∵沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,
∴∠CBD=∠DBE=18°,∠C=∠DEB=84°,
∴∠EDB=180°﹣18°﹣88°=74°.
故选:B.
二.填空题(共8小题)
11.解:∵∠CEA=60°,∠BAE=45°,
∴∠ADE=180°﹣∠CEA﹣∠BAE=75°,
∴∠BDC=∠ADE=75°,
故答案为75°.
12.解:∵在△ABC中,∠A=30°,∠B=50°,
∴∠C=180°﹣30°﹣50°=100°.
故答案为:100°
13.解:∵CD平分∠ACE,∠DCA=65°,
∴∠ACE=2∠DCA=130°,
又∵∠A=70°,
∴∠B=130°﹣70°=60°,
故答案为:60°.
14.解:给图中角标上序号,如图所示.
∵∠2+∠3+45°=180°,∠2=30°,
∴∠3=180°﹣30°﹣45°=105°,
∴∠1=∠3=105°.
故答案为:105°.
15.
解:∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∠ACD=2∠A1CD,∠ABC=2∠A1BC,
∴2∠A1CD=∠A+2∠A1BC,即∠A1CD=∠A+∠A1BC,
∴∠A1==,
由此可得∠A2010=.
故答案为:,.
16.解:∵AE是△ABC的角平分线,
∴∠CAE=∠BAC=×128°=64°,
∵AD⊥BC,
∴∠CAD=90°﹣∠C=90°﹣36°=54°,
∴∠DAE=∠CAE﹣∠CAD=64°﹣54°=10°.
故答案为:10.
17.解:如图所示:
∵∠ABC,∠ACB的角平分线交于点P,
∴∠ABP=∠PBC,∠ACP=∠PCB,
∵∠BPC=110°,
∴∠PBC+∠PCB=70°,
∴∠ABC+∠ACB=140°,
∴∠A=180°﹣140°=40°.
故答案为:40.
18.解:∵∠B=35°,∠BCA=75°,
∴∠BAC=70°,
∵由作法可知,AD是∠BAC的平分线,
∴∠CAD=∠BAC=35°,
∵由作法可知,EF是线段BC的垂直平分线,
∴∠BCF=∠B=35°,
∵∠ACF=∠ACB﹣∠BCF=40°,
∴∠α=∠CAD+∠ACF=75°,
故答案为:75.
三.解答题(共3小题)
19.解:∵AD=BD,∠A=23°,
∴∠ABD=∠A=23°,
∵BG∥EF,∠BCE=44°,
∴∠DBC=∠BCE=44°,
∴∠ABC=44°+23°=67°,
∴∠ACB=180°﹣67°﹣23°=90°.
20.解:∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∵AD是BC边上的高,
∴∠BAD=90°﹣∠ABC=90°﹣50°=40°,
∴∠DAC=∠BAC﹣∠BAD=60°﹣40°=20°.
21.证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°,
即∠A+∠B+∠C=180°.
