2018-2019九年级数学上册第一章特殊平行四边形1.3正方形的性质与判定1.3.1正方形的性质同步课时练习题(含答案)
文档属性
| 名称 | 2018-2019九年级数学上册第一章特殊平行四边形1.3正方形的性质与判定1.3.1正方形的性质同步课时练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 75.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-21 15:25:01 | ||
图片预览


文档简介
1.3.1正方形的性质
1.在四边形ABCD中,AC与BD交于O,且OA=OC,OB=OD,AB=BC,∠DAB=90°,则四边形ABCD的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2. 正方形的对称轴的条数为( )
A.1条 B.2条 C.3条 D.4条
3. 正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
4. 如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
5. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=( )
A. B.2 C.2 D.1
6. 如图,正方形ABCD中,连接BD,点O是BD的中点.若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
7. 将正方形(图①)作如下操作:第1次:分别连接各边中点(如图②),得到5个正方形;第2次:将图②左上角正方形按上述方法再分割(如图③),得到9个正方形……以此类推,根据以上操作,若要得到2017个正方形,则需要操作的次数是( )
A.502 B.503 C.504 D.505
8. 在四边形ABCD中,若AD∥BC,AD=BC,AB=BC,∠B=90°,则四边形ABCD的形状是 .
9. 已知正方形ABCD的对角线AC=4,则这个正方形的面积是____.
10. 如图,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,那么四边形DECF是 .
11. 已知正方形ABCD的对角线AC=,则正方形ABCD的周长是____.
12. 如图,正方形ABCD的对角线AC与BD相交于点O,则图中共有____个等腰直角三角形.
13. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是 .
14. 如图,已知正方形纸片ABCD,点M,N分别是AD,BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=____.
15. 如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF= .
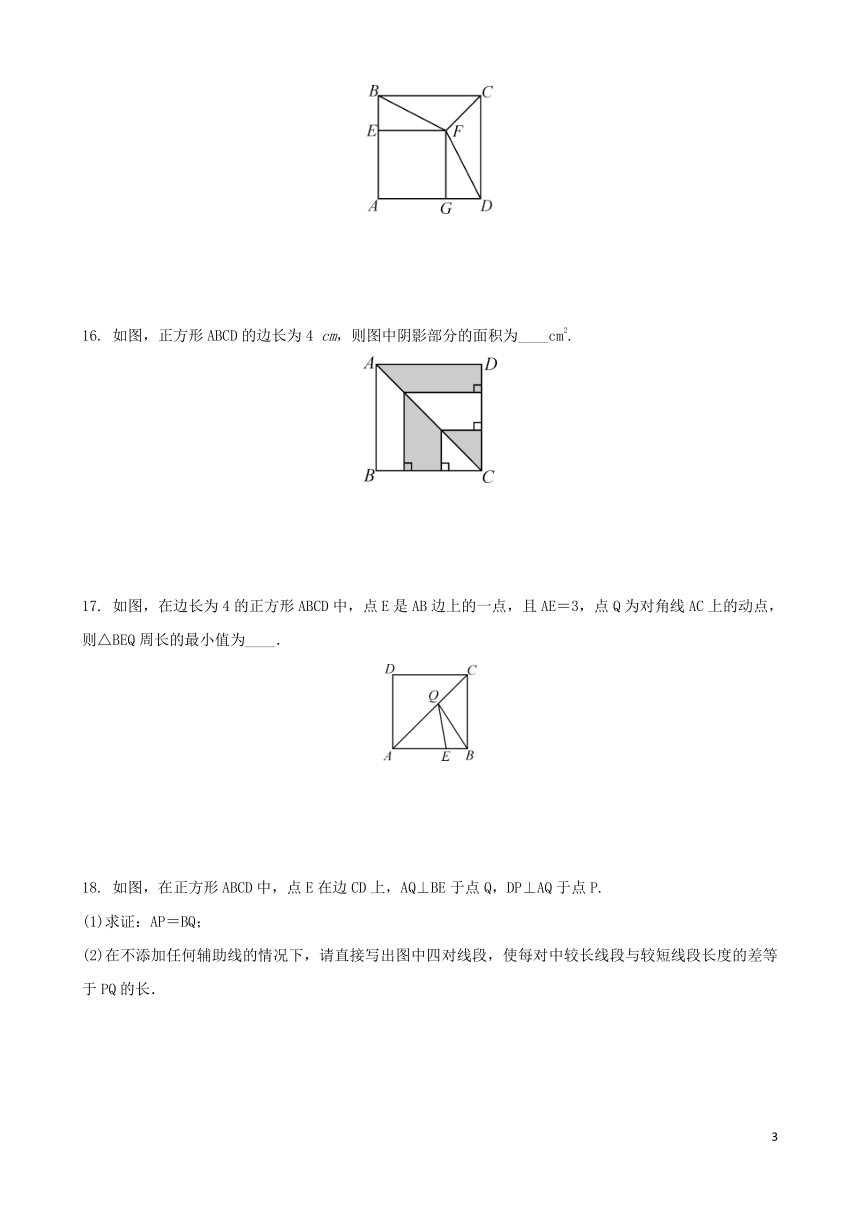
16. 如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为____cm2.
17. 如图,在边长为4的正方形ABCD中,点E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为____.
18. 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
19. 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)四边形ADCE为____;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
20. 如图所示,在正方形ABCD中,点E,F分别在BC,CD上移动,但点A到EF的距离AH始终保持与AB的长度相等,问在点E,F移动过程中:
(1)∠EAF的大小是否发生变化?请说明理由;
(2)△ECF的周长是否发生变化?请说明理由.
参考答案:
1---7 DDBCB CC
8. 正方形
9. 8
10. 正方形
11. 4
12. 8
13. 22.5°
14. 30°
15. (1) ∵四边形ABCD和AEFG都是正方形,∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,∵BE=AB-AE,DG=AD-AG,∴BE=DG,∴△BEF≌△DGF,∴BF=DF
(2)
16. 8
17. 6
18. (1)∵四边形ABCD为正方形,∴AB=AD,∠DAB=90°,
∴∠BAQ+∠DAP=90°.∵DP⊥AQ,∴∠APD=90°,
∴∠ADP+∠DAP=90°, ∴∠ADP=∠BAQ.
∵AQ⊥BE,∴∠AQB=90°,∴∠DPA=∠AQB,
∴△DAP≌△ABQ(AAS),∴AP=BQ
(2)AQ与AP,DP与AP,AQ与BQ,DP与BQ
19. (1) 矩形
(2) 当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,∴∠ACB=∠B=45°,∵AD⊥BC,
∴∠CAD=∠ACD=45°,∴DC=AD,∵四边形ADCE为矩形,
∴矩形ADCE是正方形,∴当∠BAC=90°时,四边形ADCE是一个正方形
20. (1)∠EAF的大小不变,理由如下:在正方形ABCD中,
∵AH⊥EF,∴∠AHF=∠D=90°.∵AF=AF,AH=AD,∴Rt△AHF≌Rt△ADF(HL),∴∠HAF=∠DAF.
同理 ∠HAE=∠BAE.∵∠HAF+∠DAF+∠HAE+∠BAE=90°,∴∠EAF=∠HAF+∠HAE=45°.
∴∠EAF的大小不会发生变化
(2)△ECF的周长不会发生变化,理由如下:
由(1)知Rt△AHF≌Rt△ADF,Rt△AHE≌Rt△ABE,
∴FH=FD,EH=EB.∴EF=EH+FH=EB+FD.
∴CE+CF+EF=CE+CF+EB+FD=BC+CD.
∴△ECF的周长总等于正方形ABCD边长的2倍,不会发生变化
1.在四边形ABCD中,AC与BD交于O,且OA=OC,OB=OD,AB=BC,∠DAB=90°,则四边形ABCD的形状是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2. 正方形的对称轴的条数为( )
A.1条 B.2条 C.3条 D.4条
3. 正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
4. 如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
5. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=( )
A. B.2 C.2 D.1
6. 如图,正方形ABCD中,连接BD,点O是BD的中点.若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
7. 将正方形(图①)作如下操作:第1次:分别连接各边中点(如图②),得到5个正方形;第2次:将图②左上角正方形按上述方法再分割(如图③),得到9个正方形……以此类推,根据以上操作,若要得到2017个正方形,则需要操作的次数是( )
A.502 B.503 C.504 D.505
8. 在四边形ABCD中,若AD∥BC,AD=BC,AB=BC,∠B=90°,则四边形ABCD的形状是 .
9. 已知正方形ABCD的对角线AC=4,则这个正方形的面积是____.
10. 如图,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,那么四边形DECF是 .
11. 已知正方形ABCD的对角线AC=,则正方形ABCD的周长是____.
12. 如图,正方形ABCD的对角线AC与BD相交于点O,则图中共有____个等腰直角三角形.
13. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是 .
14. 如图,已知正方形纸片ABCD,点M,N分别是AD,BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=____.
15. 如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF= .
16. 如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为____cm2.
17. 如图,在边长为4的正方形ABCD中,点E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为____.
18. 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
19. 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)四边形ADCE为____;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
20. 如图所示,在正方形ABCD中,点E,F分别在BC,CD上移动,但点A到EF的距离AH始终保持与AB的长度相等,问在点E,F移动过程中:
(1)∠EAF的大小是否发生变化?请说明理由;
(2)△ECF的周长是否发生变化?请说明理由.
参考答案:
1---7 DDBCB CC
8. 正方形
9. 8
10. 正方形
11. 4
12. 8
13. 22.5°
14. 30°
15. (1) ∵四边形ABCD和AEFG都是正方形,∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,∵BE=AB-AE,DG=AD-AG,∴BE=DG,∴△BEF≌△DGF,∴BF=DF
(2)
16. 8
17. 6
18. (1)∵四边形ABCD为正方形,∴AB=AD,∠DAB=90°,
∴∠BAQ+∠DAP=90°.∵DP⊥AQ,∴∠APD=90°,
∴∠ADP+∠DAP=90°, ∴∠ADP=∠BAQ.
∵AQ⊥BE,∴∠AQB=90°,∴∠DPA=∠AQB,
∴△DAP≌△ABQ(AAS),∴AP=BQ
(2)AQ与AP,DP与AP,AQ与BQ,DP与BQ
19. (1) 矩形
(2) 当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,∴∠ACB=∠B=45°,∵AD⊥BC,
∴∠CAD=∠ACD=45°,∴DC=AD,∵四边形ADCE为矩形,
∴矩形ADCE是正方形,∴当∠BAC=90°时,四边形ADCE是一个正方形
20. (1)∠EAF的大小不变,理由如下:在正方形ABCD中,
∵AH⊥EF,∴∠AHF=∠D=90°.∵AF=AF,AH=AD,∴Rt△AHF≌Rt△ADF(HL),∴∠HAF=∠DAF.
同理 ∠HAE=∠BAE.∵∠HAF+∠DAF+∠HAE+∠BAE=90°,∴∠EAF=∠HAF+∠HAE=45°.
∴∠EAF的大小不会发生变化
(2)△ECF的周长不会发生变化,理由如下:
由(1)知Rt△AHF≌Rt△ADF,Rt△AHE≌Rt△ABE,
∴FH=FD,EH=EB.∴EF=EH+FH=EB+FD.
∴CE+CF+EF=CE+CF+EB+FD=BC+CD.
∴△ECF的周长总等于正方形ABCD边长的2倍,不会发生变化
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
