2.1.1三角形的三边关系-试卷

21世纪教育网 –中小学教育资源及组卷应用平台
2.1.1三角形的三边关系
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题8分）
1．三角形是（ ）
A. 连接任意三角形组成的图形
B. 由不在同一条直线上的三条线段首尾顺次相接所组成的的图形
C. 由三条线段组成的图形
D. 以上说法均不对
2．下面四个图形中，线段AD是△ABC的高的是( )
A. B. C. D.
3．如图，AE是△ABC的中线，已知EC＝4，DE＝2，则BD的长为(　　)
A. 2 B. 3 C. 4 D. 6
4．已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（　　 ）
A. 5 B. 6 C. 11 D. 16
5．如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（ ）
A. AB=2BF B. ∠ACE=∠ACB C. AE=BE D. CD⊥BE
二．填空题（共4小题，每题5分）
6．如图，∠C在三角形中所对的边是________________.
7．如果一个三角形的三条边长分别为5，7，x，则x的取值范围是______________.
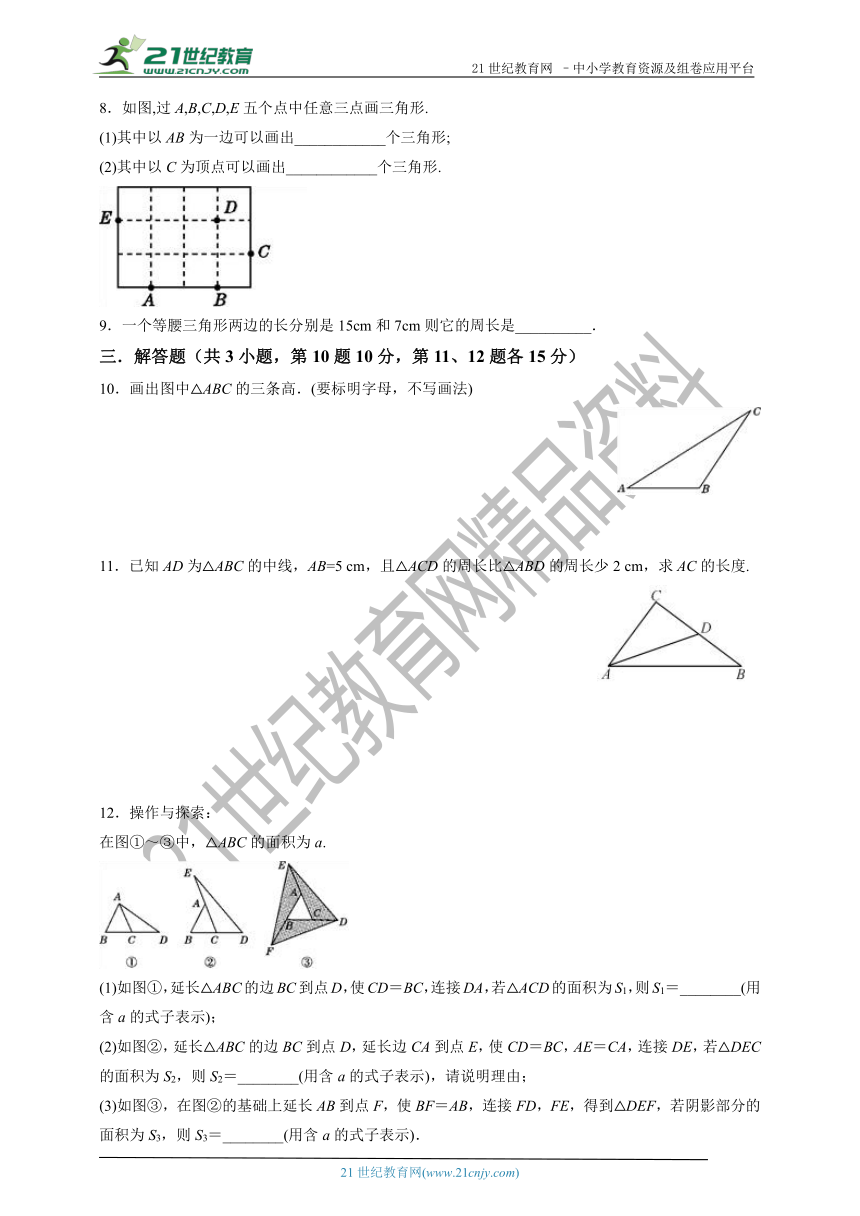
8．如图,过A,B,C,D,E五个点中任意三点画三角形.
(1)其中以AB为一边可以画出____________个三角形;
(2)其中以C为顶点可以画出____________个三角形.
9．一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
三．解答题（共3小题，第10题10分，第11、12题各15分）
10．画出图中△ABC的三条高．(要标明字母，不写画法)
11．已知AD为△ABC的中线，AB=5 cm，且△ACD的周长比△ABD的周长少2 cm，求AC的长度.
12．操作与探索：
在图①～③中，△ABC的面积为a.
(1)如图①，延长△ABC的边BC到点D，使CD＝BC，连接DA，若△ACD的面积为S1，则S1＝________(用含a的式子表示)；
(2)如图②，延长△ABC的边BC到点D，延长边CA到点E，使CD＝BC，AE＝CA，连接DE，若△DEC的面积为S2，则S2＝________(用含a的式子表示)，请说明理由；
(3)如图③，在图②的基础上延长AB到点F，使BF＝AB，连接FD，FE，得到△DEF，若阴影部分的面积为S3，则S3＝________(用含a的式子表示)．
试题解析
1．B
【解析】因为三角形的定义是：由不在同一条直线上的三条线段首尾顺次相接所成的图形．
故选B．
2．D
【解析】根据三角形高的定义：从顶点向对边作垂线，垂线段就是对应边上的高可判断.
解:A.线段AD与BC不垂直，所以不是△ABC的高；
B.线段AD与BC不垂直，所以不是△ABC的高；
C.线段AD与BC不垂直，所以不是△ABC的高；
D.线段AD与BC垂直，所以是△ABC的高.
故选：D.
3．A
【解析】∵AE是△ABC的中线，EC=4，
∴BE=EC=4，
∵DE=2，
∴BD=BE-DE=4-2=2．
故选A．
4．C
【解析】设第三边为x，由三角形三边的性质，66．AE，BD，AB
【解析】在△ABC中, ∠C的对边是AB; 在△ACE中, ∠C的对边是AE在△BCD中, ∠C的对边是BD;
故答案为: AE，BD，AB
7．2【解析】根据三角形的三边关系,再结合已知两条边的长度,就能求出第三边的范围.
解：根据构成三角形的三边关系,得
x＞7-5且x＜7+5
即2＜x＜12
则x的取值范围是2＜x＜12.故答案为：28．3，6
【解析】（1）以AB为一边可以画出3个三角形为：△ABE，△ABD，△ABC；
（2）以C为顶点可以画出6个三角形为：△ABC，△BCD，△BCE，△ADC，△DEC，△ACE．
故答案为：3；6．
9．37cm
【解析】要分情况讨论并利用三角形三边的关系进行判定能否组成三角形.
解：①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm.
10．画图见解析.
【解析】按照“过一点作已知直线的垂线”进行作图即可，需注意AB，BC边上的高在三角形的外部
解：如图．
11．3cm
【解析】由AD是△ABC的中线可得CD=BD，从而可得
C△ABD-C△ACD=(AB+AD+BD)-(AC+AD+CD)=AB-AC=2，由AB=5，可解得AC=3（cm）.
解：∵AD为△ABC的中线，
∴BD=CD.
∵△ACD的周长比△ABD的周长少2 cm，
∴(AB+BD+AD)-(AC+AD+CD)=AB-AC=2 cm，
∴AC=AB-2=5-2=3(cm).
12．（1）a；（2）2a；（3）6a.
【解析】（1）过点A作AH⊥BD于H，如图1，由于△ACD与△ABC底相等、高相同，因此它们的面积相等，问题得以解决；
（2）连接AD，如图2，同（1）可求出△EAD的面积，就可解决问题；
（3）如图3，同（2）可求出△EAF和△FBD的面积，问题得以解决.
解：（1）过点A作AH⊥BD于H，如图1，
∵BC=CD，S△ABC=BC AH=a，S△ACD=CD AH，
∴S1=S△ACD=S△ABC=a．
故答案为a．
（2）连接AD，如图2，
同理可得S△EAD=S△ACD=S△ABC=a，
∴S2=S△ECD=a+a=2a．
故答案为2a．
（3）同（2）可得
S△FBD=S△EAF=S△ECD=2a，
∴S3=6a，
故答案为6a
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)