山东省武城县二中2018-2019学年高一上学期入学考试数学试卷
文档属性
| 名称 | 山东省武城县二中2018-2019学年高一上学期入学考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 147.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-22 09:00:21 | ||
图片预览




文档简介
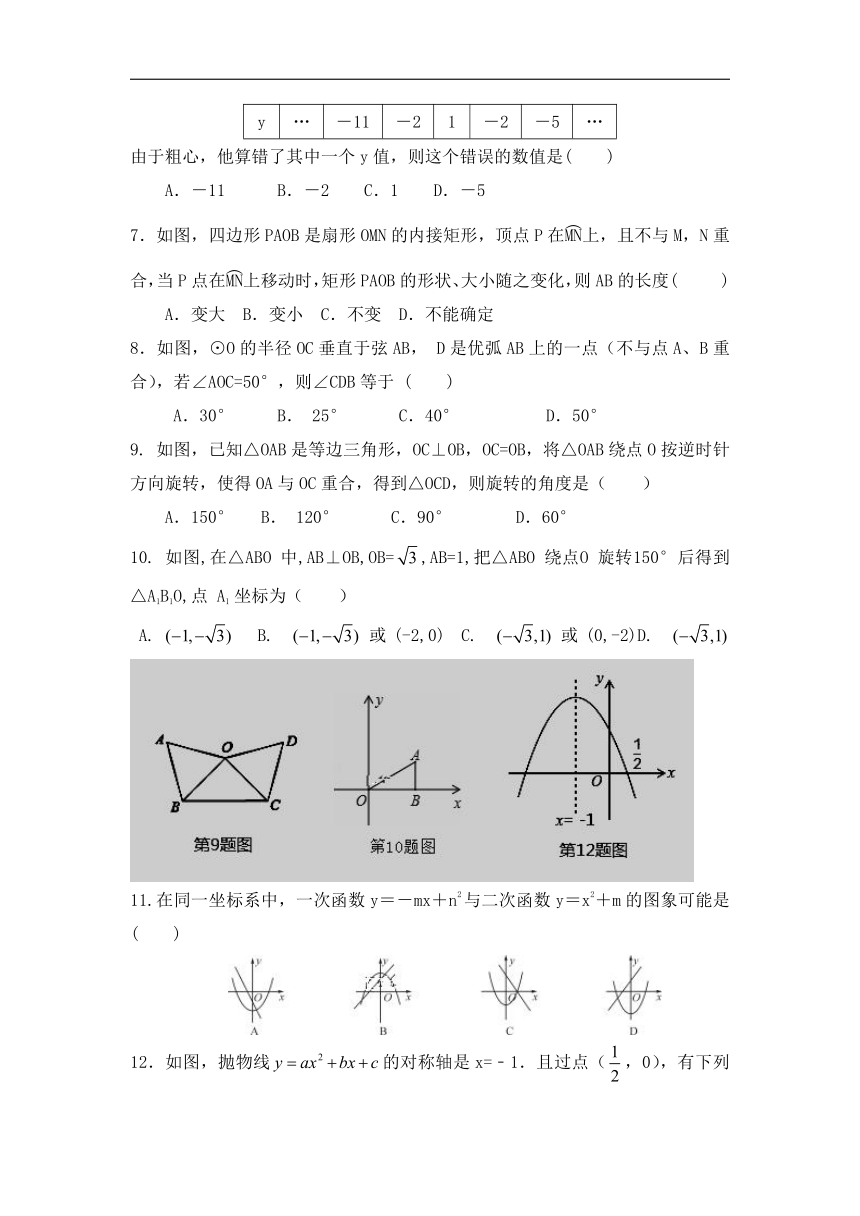
高一数学试题
满分:150分 时间:120分钟
一、选择题(每小题4分,共48分)
1.下列标志既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法正确的是( )
A.长度相等的两条弧是等弧 ?B.平分弦的直径垂直于弦
C.直径是同一个圆中最长的弦 D.过三点能确定一个圆
3.用配方法解一元二次方程,则方程可化为( )
A. B. C. ?D.
4.将抛物线y=x24先向右平移2个单位,再向上平移2个单位,得到的抛物线的表达式是( )
A.y=(x+2)2+2 B.y=(x2)22 C.y=(x2)2+2 D.y=(x+2)22
5.如图,在⊙O中,弦AB的长为10,圆周角∠ACB=45°,则这个圆的直径为( )
A.5 B.10 C.15 D.20
(第5题图) (第7题图) (第8题图)
6.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x
…
-2
-1
0
1
2
…
y
…
-11
-2
1
-2
-5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,则AB的长度( )
A.变大 B.变小 C.不变 D.不能确定
8.如图,⊙O的半径OC垂直于弦AB, D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于 ( )
A.30° B. 25° C.40° D.50°
9. 如图,已知△OAB是等边三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )
A.150° B. 120° C.90° D.60°
10. 如图,在△ABO 中,AB⊥OB,OB=,AB=1,把△ABO 绕点O 旋转150°后得到△A1B1O,点 A1 坐标为( )
A. B. 或(-2,0) C. 或(0,-2)D.
11.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
12.如图,抛物线的对称轴是x=﹣1.且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②④ D.①③
二、填空题(每小题4分,共24分)
13.反比例函数y=(m+2)的图象分布在第二、四象限内,则m的值为 .
14.设a, b是方程x2+x﹣9=0的两个实数根,则a2+2a+b的值为 .
15.如图,小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m.已知DE=30cm,EF=20cm,那么树AB的高度等于 m.
16.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
17.平面直角坐标系内一点P(﹣5,1)关于原点对称的点的坐标是 .
18.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根.其中正确的有 .(填正确结论的序号)
(15题图) (16题图)
三、解答题(共78分)
19.(本题10分)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.
(1)求的值及B点坐标;
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
20.(本题10分)某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
21.(本题10分)如图,已知AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.2
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
22.(本题12分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
23.(本题10分)矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,AE=10,求DF的长.
24.(本题12分)如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
25.(本题14分)如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60o. (1)求⊙O的直径; (2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切; (3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0
数学参考答案及评分意见
选择题(每题4分,共48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
A
B
B
D
C
B
A
B
D
D
二、填空题(每小题4分,共24分)
13.-3 14.8 15.5.4 16.10 17.(5,-1) 18. ①③④
三、解答题(共78分)
19. (本题10分)
(1)k=8, B(-4,-2)
(2)x>4或-4<x<0
20. (本题10分)
(1)根据题意得:20÷36360=200(人),
则这次被调查的学生共有200人;
故答案为:200; (2)喜欢羽毛球的人数是:200?20?80?40=60(人),补全图形,如图所示:
(3)列表如下:
甲
乙
丙
丁
甲
???
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
???
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
???
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
???
所有等可能的结果为12种,其中符合要求的只有2种,
则P=.
21. (本题10分)
(1)证明:如图,连接OC,
∵EF是过点C的⊙O的切线,
∴OC⊥EF.
又∵AD⊥EF,
∴OC∥AD.∴∠OCA=∠CAD.
又∵OA=OC,
∴∠OCA=∠BAC.∴∠BAC=∠CAD.
(2)解:∵∠B=30°.
∴∠AOC=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
22. (本题12分)
解:(1)由题意得出:
w=(x﹣20)?y
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
故w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程﹣2(x﹣30)2+200=150.
解得?x1=25,x2=35.????
∵35>28,
∴x2=35不符合题意,应舍去.??
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
23. (本题10分)
(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠B=∠AFD=90°,
∴△ABE∽△DFA;
(2)解:由(1)可知△ABE∽△DFA,
∴=,
∵AB=6,AD=12,AE=10,
∴=,
解得DF=7.2.
24. (本题12分)
解:(1)由题意可得:﹣(﹣1)2+2×(﹣1)+c=0,
解得:c=3,
∴y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4);
(2)∵A(﹣1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),
∴EM=1,BN=2,
∵EM∥BN,
∴△EMF∽△BNF,
∴=()2=()2=.
25(本题14分)
解:(1)∵AB是⊙O的直径 ∴∠ACB=90o ∵∠ABC=60o ∴∠BAC=180o-∠ACB-∠ABC=30o ∴AB=2BC=4cm,即⊙O的直径为4cm; (2)如图,连结OC.? ∵CD切⊙O于点C, ∴CD⊥CO ∴∠OCD=90o ∵∠BAC=30o ∴∠COD=2∠BAC=60o. ∴∠D=180o-∠COD-∠OCD=30o ∴OD=2OC=4cm ∴BD=OD-OB=4-2=2cm ∴当BD长为2cm时,CD与⊙O相切; (3)根据题意,得BE=(4-2t)cm,BF=tcm;? 如图,当∠EFB=90o时,△BEF为直角三角形, ∵∠EFB=∠ACB,∠B=∠B ∴△BEF∽△BAC ∴,即,解得t=1. 如图,当∠FEB=90o时,△BEF为直角三角形, ∵∠FEB=∠ACB,∠B=∠B, ∴△BEF∽△BCA. ∴,即,解得t=1.6.? ∴当t=1s或t=1.6s时,△BEF为直角三角形.
满分:150分 时间:120分钟
一、选择题(每小题4分,共48分)
1.下列标志既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法正确的是( )
A.长度相等的两条弧是等弧 ?B.平分弦的直径垂直于弦
C.直径是同一个圆中最长的弦 D.过三点能确定一个圆
3.用配方法解一元二次方程,则方程可化为( )
A. B. C. ?D.
4.将抛物线y=x24先向右平移2个单位,再向上平移2个单位,得到的抛物线的表达式是( )
A.y=(x+2)2+2 B.y=(x2)22 C.y=(x2)2+2 D.y=(x+2)22
5.如图,在⊙O中,弦AB的长为10,圆周角∠ACB=45°,则这个圆的直径为( )
A.5 B.10 C.15 D.20
(第5题图) (第7题图) (第8题图)
6.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x
…
-2
-1
0
1
2
…
y
…
-11
-2
1
-2
-5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,则AB的长度( )
A.变大 B.变小 C.不变 D.不能确定
8.如图,⊙O的半径OC垂直于弦AB, D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于 ( )
A.30° B. 25° C.40° D.50°
9. 如图,已知△OAB是等边三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )
A.150° B. 120° C.90° D.60°
10. 如图,在△ABO 中,AB⊥OB,OB=,AB=1,把△ABO 绕点O 旋转150°后得到△A1B1O,点 A1 坐标为( )
A. B. 或(-2,0) C. 或(0,-2)D.
11.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
12.如图,抛物线的对称轴是x=﹣1.且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②④ D.①③
二、填空题(每小题4分,共24分)
13.反比例函数y=(m+2)的图象分布在第二、四象限内,则m的值为 .
14.设a, b是方程x2+x﹣9=0的两个实数根,则a2+2a+b的值为 .
15.如图,小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m.已知DE=30cm,EF=20cm,那么树AB的高度等于 m.
16.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
17.平面直角坐标系内一点P(﹣5,1)关于原点对称的点的坐标是 .
18.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根.其中正确的有 .(填正确结论的序号)
(15题图) (16题图)
三、解答题(共78分)
19.(本题10分)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.
(1)求的值及B点坐标;
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
20.(本题10分)某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
21.(本题10分)如图,已知AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.2
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
22.(本题12分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
23.(本题10分)矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,AE=10,求DF的长.
24.(本题12分)如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
25.(本题14分)如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60o. (1)求⊙O的直径; (2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切; (3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0
选择题(每题4分,共48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
A
B
B
D
C
B
A
B
D
D
二、填空题(每小题4分,共24分)
13.-3 14.8 15.5.4 16.10 17.(5,-1) 18. ①③④
三、解答题(共78分)
19. (本题10分)
(1)k=8, B(-4,-2)
(2)x>4或-4<x<0
20. (本题10分)
(1)根据题意得:20÷36360=200(人),
则这次被调查的学生共有200人;
故答案为:200; (2)喜欢羽毛球的人数是:200?20?80?40=60(人),补全图形,如图所示:
(3)列表如下:
甲
乙
丙
丁
甲
???
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
???
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
???
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
???
所有等可能的结果为12种,其中符合要求的只有2种,
则P=.
21. (本题10分)
(1)证明:如图,连接OC,
∵EF是过点C的⊙O的切线,
∴OC⊥EF.
又∵AD⊥EF,
∴OC∥AD.∴∠OCA=∠CAD.
又∵OA=OC,
∴∠OCA=∠BAC.∴∠BAC=∠CAD.
(2)解:∵∠B=30°.
∴∠AOC=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
22. (本题12分)
解:(1)由题意得出:
w=(x﹣20)?y
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
故w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程﹣2(x﹣30)2+200=150.
解得?x1=25,x2=35.????
∵35>28,
∴x2=35不符合题意,应舍去.??
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
23. (本题10分)
(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠B=∠AFD=90°,
∴△ABE∽△DFA;
(2)解:由(1)可知△ABE∽△DFA,
∴=,
∵AB=6,AD=12,AE=10,
∴=,
解得DF=7.2.
24. (本题12分)
解:(1)由题意可得:﹣(﹣1)2+2×(﹣1)+c=0,
解得:c=3,
∴y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4);
(2)∵A(﹣1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),
∴EM=1,BN=2,
∵EM∥BN,
∴△EMF∽△BNF,
∴=()2=()2=.
25(本题14分)
解:(1)∵AB是⊙O的直径 ∴∠ACB=90o ∵∠ABC=60o ∴∠BAC=180o-∠ACB-∠ABC=30o ∴AB=2BC=4cm,即⊙O的直径为4cm; (2)如图,连结OC.? ∵CD切⊙O于点C, ∴CD⊥CO ∴∠OCD=90o ∵∠BAC=30o ∴∠COD=2∠BAC=60o. ∴∠D=180o-∠COD-∠OCD=30o ∴OD=2OC=4cm ∴BD=OD-OB=4-2=2cm ∴当BD长为2cm时,CD与⊙O相切; (3)根据题意,得BE=(4-2t)cm,BF=tcm;? 如图,当∠EFB=90o时,△BEF为直角三角形, ∵∠EFB=∠ACB,∠B=∠B ∴△BEF∽△BAC ∴,即,解得t=1. 如图,当∠FEB=90o时,△BEF为直角三角形, ∵∠FEB=∠ACB,∠B=∠B, ∴△BEF∽△BCA. ∴,即,解得t=1.6.? ∴当t=1s或t=1.6s时,△BEF为直角三角形.
同课章节目录
