人教版选修2-3第一章第二节排列与组合的应用课件(33张ppt)
文档属性
| 名称 | 人教版选修2-3第一章第二节排列与组合的应用课件(33张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-23 00:00:00 | ||
图片预览











文档简介
课件33张PPT。
排列与组合的应用(1)使学生掌握排列组合数的计算公式,加深对排列组合数公式的理解及灵活运用能力?。
(2)会用排列数公式和组合数公式解决实际问题.培养学生理论联系实际的能力。???
(3)通过合作探究学习,培养学生的合作能力及自主学习能力教学目标:基
本
原
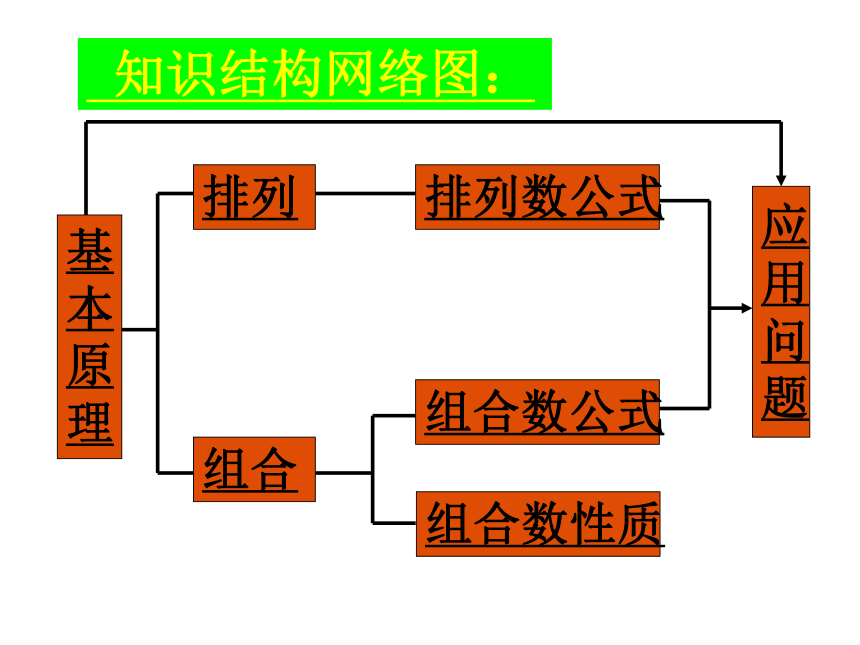
理组合排列排列数公式组合数公式组合数性质应
用
问
题 知识结构网络图:排列组合应用题解法综述计数问题中排列组合问题是最常见的,由于其解法往往是构造性的, 因此方法灵活多样, 不同解法导致问题难易变化也较大,而且解题过程出现“重复”和“遗漏”的错误较难自检发现。因而对这类问题归纳总结,并把握一些常见解题模型是必要的。从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.2.组合的定义:从n个不同元素中,任取m个元素,并成一组,叫做从n个不同元素中取出m个元素的一个组合.
3.排列数公式:4.组合数公式:1.排列的定义:排列与组合的区别与联系:与顺序有关为排列问题,与顺序无关的为组合问题.复习导入题型一 排列应用题
例1、有5个同学排队照相,求:
(1)甲、乙两个同学必须相邻的排法有多少种?
(2)甲、乙、丙3个同学互不相邻的排法有多少种?
(3)乙不能站在甲前面,丙不能站在乙前面的排法有多少种?
(4)甲不站在中间位置,乙不站在两端两个位置的排法有多少种?基本题型突破排列应用题小结1.优先法:先特殊后一般2.捆绑法:元素相邻3.插空法:元素不相邻4.其它方法:元素限制条件多--间接法例2 按下列要求分配6本不同的书,各有多少种不同的分配方式?
(1)分成三份,1份1本,1份2本,1份3本;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
(3)平均分成三份,每份2本;
(4)平均分配给甲、乙、丙三人,每人2本;
(5)分成三份,1份4本,另外两份每份1本;
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本;
(7)甲得1本,乙得1本,丙得4本.
【思路】 这是一个分配问题,解题的关键是搞清事件是否与
顺序有关,对于平均分组问题更要注意顺序,避免计数的重复
或遗漏.题型二 组合应用题 均匀分组与不均匀分组、无序分组与有序分组是组合问题常见题型.解决此类问题的关键是正确判断分组是均匀分组还是不均匀分组,无序均匀分组要除以均匀组数的阶乘数;还要充分考虑到是否与顺序有关,有序分组要在无序分组的基础上乘以分组数的阶乘数.组合应用题小结例3.有5个不同的小球,装入4个不同的盒内,每盒至少
装一个球,共有多少不同的装法.解:第一步从5个球中选出2个组成复合元共有 种方法.再把5个元素(包含一个复合元素)装入4个不同的盒内有 种方法.根据分步计数原理装球的方法共有 .小结:解决排列组合混合问题,先选后排是最基本的指导思想.三、排列组合混合问题应用题 有限制条件的排列组合综合问题是主要考查方向.解决此类问题要遵循“谁特殊谁_______”的原则,采取分类或分步,或用间接法处理;对于选排列问题可采用先____后______的方法,分配问题的一般思路是先__________再分配.排列组合问题小结:优先选排选取重点题型突破:
一、名额分配问题(隔板法策略)
例4、 8个相同的小球放入5个不同盒子中,每盒不空的放法
共有________种.变式训练: 有5个大学保送名额,计划分到3个班级每班至少一个名额,
有多少种不同的分法? 小结:
(1)定数量:确定名额的个数、分成的组数以及各组名额
的数量.
(2)定空位:将元素排成一列,确定可插隔板的空位数.
(3)插隔板:确定需要的隔板个数,根据组数要求,插入隔板,
利用组合数求解不同的分法种数.二.实际操作穷举策略例5.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,.有多少投法?
解:从5个球中取出2个与盒子对号有_____种还剩下3球3盒序号不能对应,2 给图中区域涂色,要求相邻区域不同色,现有4种可选颜色,则不同的着色方法有____种72变式训练: 对于条件比较复杂的排列组合问题,不易用公式进行运算,往往利用穷举法或画出树状图会收到意想不到的结果小结:三.构造模型策略例6、马路上有编号为1,2,3,4,5,6,7,8,9的九只路灯,现要关掉其中的3盏,但不能关掉相邻的2盏或3盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种?解:把此问题当作一个排队模型在6盏亮灯的5个空隙中插入3个不亮的灯有________ 种某排共有10个座位,若4人就坐,每人左右两边都有空位,那么不同的坐法有多少种?120变式训练: 一些不易理解的排列组合题如果能转化为非常熟悉的模型,如占位填空模型,排队模型,装盒模型等,可使问题直观解决。小结:四、 复杂问题分解策略
例7正方体的8个顶点可连成多少对异面直线?
解:我们先从8个顶点中任取4个顶点构成四
体共有体共__________
3174 25人排成5×5方队,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?解:将这个问题退化成9人排成3×3方队,现从中选3人,要求3人不在同一行也不在同一列,有多少选法.这样每行必有1人从其中的一行中选取1人后,把这人所在的行列都划掉,变式训练:从5×5方队中选取3行3列有_____选法
所以从5×5方队选不在同一行也不在同
一列的3人有__________________选法。如此继续下去.从3×3方队中选3人的方法有___________种。再从5×5方队选出3×3方队便可解决问题小结: 复杂问题分解策略是排列组合问题的一种最
基本的解题策略,把一个复杂问题分解成几
个小问题逐一解决,然后依据问题分解后的
结构,用分类计数原理和分步计数原理将问
题合成,从而得到问题的答案 ,每个比较复
杂的问题都要用到这种解题策略3、10个相同的球装5个盒中,每盒至少一个,有多少种装法?4、7人排队,其中甲乙丙3人顺序一定共有多少种不同的排法?解析:设想有7把椅子让除甲乙丙以外的四人就坐共有 种方法,其余的三个位置甲乙丙共有 种坐法,则共有方法。 种1课堂巩固训练 同一寝室4人,每人写一张贺年卡集中起来,然后每人各拿一张别人的贺年卡,则四张贺年卡不同的分配方式有多少种?5张贺卡?
6张?有什么规律?思考题课堂小结(5).实际操作穷举策略(3).排列组合混合问题先选后排策略(4).元素相同问题隔板策略(2).平均分组问题除法策略(6).构造模型策略(1).合理分类与分步策略(7).复杂问题分解策略2、(选做题) 3成人2小孩乘船游玩,1号船最多乘3人, 2号船最多乘2人,3号船只能乘1人,他们任选2只船或3只船,但小孩不能单独乘一只船,这3人共有多少乘船方法?布置作业1、(必做题)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A
与产品C不相邻,则不同的摆法有几种?谢谢大家!
排列与组合的应用(1)使学生掌握排列组合数的计算公式,加深对排列组合数公式的理解及灵活运用能力?。
(2)会用排列数公式和组合数公式解决实际问题.培养学生理论联系实际的能力。???
(3)通过合作探究学习,培养学生的合作能力及自主学习能力教学目标:基
本
原
理组合排列排列数公式组合数公式组合数性质应
用
问
题 知识结构网络图:排列组合应用题解法综述计数问题中排列组合问题是最常见的,由于其解法往往是构造性的, 因此方法灵活多样, 不同解法导致问题难易变化也较大,而且解题过程出现“重复”和“遗漏”的错误较难自检发现。因而对这类问题归纳总结,并把握一些常见解题模型是必要的。从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.2.组合的定义:从n个不同元素中,任取m个元素,并成一组,叫做从n个不同元素中取出m个元素的一个组合.
3.排列数公式:4.组合数公式:1.排列的定义:排列与组合的区别与联系:与顺序有关为排列问题,与顺序无关的为组合问题.复习导入题型一 排列应用题
例1、有5个同学排队照相,求:
(1)甲、乙两个同学必须相邻的排法有多少种?
(2)甲、乙、丙3个同学互不相邻的排法有多少种?
(3)乙不能站在甲前面,丙不能站在乙前面的排法有多少种?
(4)甲不站在中间位置,乙不站在两端两个位置的排法有多少种?基本题型突破排列应用题小结1.优先法:先特殊后一般2.捆绑法:元素相邻3.插空法:元素不相邻4.其它方法:元素限制条件多--间接法例2 按下列要求分配6本不同的书,各有多少种不同的分配方式?
(1)分成三份,1份1本,1份2本,1份3本;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
(3)平均分成三份,每份2本;
(4)平均分配给甲、乙、丙三人,每人2本;
(5)分成三份,1份4本,另外两份每份1本;
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本;
(7)甲得1本,乙得1本,丙得4本.
【思路】 这是一个分配问题,解题的关键是搞清事件是否与
顺序有关,对于平均分组问题更要注意顺序,避免计数的重复
或遗漏.题型二 组合应用题 均匀分组与不均匀分组、无序分组与有序分组是组合问题常见题型.解决此类问题的关键是正确判断分组是均匀分组还是不均匀分组,无序均匀分组要除以均匀组数的阶乘数;还要充分考虑到是否与顺序有关,有序分组要在无序分组的基础上乘以分组数的阶乘数.组合应用题小结例3.有5个不同的小球,装入4个不同的盒内,每盒至少
装一个球,共有多少不同的装法.解:第一步从5个球中选出2个组成复合元共有 种方法.再把5个元素(包含一个复合元素)装入4个不同的盒内有 种方法.根据分步计数原理装球的方法共有 .小结:解决排列组合混合问题,先选后排是最基本的指导思想.三、排列组合混合问题应用题 有限制条件的排列组合综合问题是主要考查方向.解决此类问题要遵循“谁特殊谁_______”的原则,采取分类或分步,或用间接法处理;对于选排列问题可采用先____后______的方法,分配问题的一般思路是先__________再分配.排列组合问题小结:优先选排选取重点题型突破:
一、名额分配问题(隔板法策略)
例4、 8个相同的小球放入5个不同盒子中,每盒不空的放法
共有________种.变式训练: 有5个大学保送名额,计划分到3个班级每班至少一个名额,
有多少种不同的分法? 小结:
(1)定数量:确定名额的个数、分成的组数以及各组名额
的数量.
(2)定空位:将元素排成一列,确定可插隔板的空位数.
(3)插隔板:确定需要的隔板个数,根据组数要求,插入隔板,
利用组合数求解不同的分法种数.二.实际操作穷举策略例5.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,.有多少投法?
解:从5个球中取出2个与盒子对号有_____种还剩下3球3盒序号不能对应,2 给图中区域涂色,要求相邻区域不同色,现有4种可选颜色,则不同的着色方法有____种72变式训练: 对于条件比较复杂的排列组合问题,不易用公式进行运算,往往利用穷举法或画出树状图会收到意想不到的结果小结:三.构造模型策略例6、马路上有编号为1,2,3,4,5,6,7,8,9的九只路灯,现要关掉其中的3盏,但不能关掉相邻的2盏或3盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种?解:把此问题当作一个排队模型在6盏亮灯的5个空隙中插入3个不亮的灯有________ 种某排共有10个座位,若4人就坐,每人左右两边都有空位,那么不同的坐法有多少种?120变式训练: 一些不易理解的排列组合题如果能转化为非常熟悉的模型,如占位填空模型,排队模型,装盒模型等,可使问题直观解决。小结:四、 复杂问题分解策略
例7正方体的8个顶点可连成多少对异面直线?
解:我们先从8个顶点中任取4个顶点构成四
体共有体共__________
3174 25人排成5×5方队,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?解:将这个问题退化成9人排成3×3方队,现从中选3人,要求3人不在同一行也不在同一列,有多少选法.这样每行必有1人从其中的一行中选取1人后,把这人所在的行列都划掉,变式训练:从5×5方队中选取3行3列有_____选法
所以从5×5方队选不在同一行也不在同
一列的3人有__________________选法。如此继续下去.从3×3方队中选3人的方法有___________种。再从5×5方队选出3×3方队便可解决问题小结: 复杂问题分解策略是排列组合问题的一种最
基本的解题策略,把一个复杂问题分解成几
个小问题逐一解决,然后依据问题分解后的
结构,用分类计数原理和分步计数原理将问
题合成,从而得到问题的答案 ,每个比较复
杂的问题都要用到这种解题策略3、10个相同的球装5个盒中,每盒至少一个,有多少种装法?4、7人排队,其中甲乙丙3人顺序一定共有多少种不同的排法?解析:设想有7把椅子让除甲乙丙以外的四人就坐共有 种方法,其余的三个位置甲乙丙共有 种坐法,则共有方法。 种1课堂巩固训练 同一寝室4人,每人写一张贺年卡集中起来,然后每人各拿一张别人的贺年卡,则四张贺年卡不同的分配方式有多少种?5张贺卡?
6张?有什么规律?思考题课堂小结(5).实际操作穷举策略(3).排列组合混合问题先选后排策略(4).元素相同问题隔板策略(2).平均分组问题除法策略(6).构造模型策略(1).合理分类与分步策略(7).复杂问题分解策略2、(选做题) 3成人2小孩乘船游玩,1号船最多乘3人, 2号船最多乘2人,3号船只能乘1人,他们任选2只船或3只船,但小孩不能单独乘一只船,这3人共有多少乘船方法?布置作业1、(必做题)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A
与产品C不相邻,则不同的摆法有几种?谢谢大家!
