2018年八年级物理上册1.3长度和时间测量的应用练习新版粤教沪版
文档属性
| 名称 | 2018年八年级物理上册1.3长度和时间测量的应用练习新版粤教沪版 |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-08-23 22:09:30 | ||
图片预览




文档简介
1.3 长度和时间测量的应用
图1-3-1
一 长度测量的特殊方法
测量对象
器材
图示
方法
地图上铁路线、公路线、河流的长度
弹性不大的棉线、刻度尺
________法
纸张、硬币、邮票的厚度,头发丝、铜丝的直径
刻度尺、铅笔
________法
球、硬币的直径
三角板、刻度尺
________法
操场的长度
自行车、细线、刻度尺
________法
二 用量筒或量杯测液体和固体的体积
1.用量筒测液体的体积
(1)使用前:观察量筒的__________和__________。
(2)使用:把液体缓慢倒入量筒。
(3)读数:读数时,视线应与液面的______________________相平。
[说明] 量筒上所标的单位通常是毫升(mL),1 mL=1 cm3=1×10-6 m3 。量筒呈圆柱形,体积与高度成正比,刻度均匀,没有零刻度线。量杯的刻度线分布不均匀(上密下疏)。
2.用量筒测形状不规则小块固体的体积
(1)先在量筒内倒入________的水,读出量筒内水的体积V1。
(2)把形状不规则的物体用细线系好,轻轻放入量筒内(浸没),读出量筒内液面对应的示数V2。
(3)被测物体的体积V=____________。
三 长度和时间的估测
1.记下你身上的“尺”和“表”
尺
身高
一步
一拃
长度
表
脉搏跳动60次
正常呼吸20次
时间
要估测一个物体的长度,首先要对单位长度有具体的感性认识,可以找一些具体物体的长度来帮助认识和记忆。例如,中学生手指甲的厚度约0.5 mm,手指厚度约1 cm,手掌宽度约1 dm等,充分利用这些已知长度,对一些物体的长度进行估测。
2.古代人用日晷、沙漏、滴漏等来测量时间,现实生活中可以用脉搏来估测时间。
类型一 长度的特殊测量
例1 如图1-3-2所示是小明同学利用一根粗细均匀的铅笔、刻度尺来测量细铁丝的直径。请你帮助小明完成下面的表格。
线圈长度/cm
线圈圈数
铜线的直径/cm
32
图1-3-2
[方法指导]长度的特殊测量方法
(1)累积法:把若干个相同的微小量“累积”起来,变得可直接测量,将测出的总量除以累积的个数,便得到微小量。如测量一张纸的厚度等;(2)平移法:借助辅助器材(如三角板、直尺)把不可直接测量的长度“平移”到刻度尺上,从而可直接测出该长度。如测硬币直径等;(3)以直代曲法:把不能直接测量的曲线变为直线,再用刻度尺测量。如测地图上一段距离的长度等;(4)滚轮法:用已知周长的滚轮在较长的曲线上滚动,记下滚过的圈数,再用滚过的圈数乘轮子的周长,就可得到曲线的长度。如汽车、摩托车上的里程表。
类型二 长度和时间的估测
例2 中华人民共和国的国旗为长方形五星红旗,如图1-3-3所示是天安门广场升旗仪式的场景,根据图片提供的信息估测该国旗的宽度,下列数据最接近实际情况的是( )
图1-3-3
A.1.8 m B.3.3 m
C.4.8 m D.5.5 m
[方法指导]熟悉身边数据,估测长度与时间
此类题需要熟悉并利用身边的一些相关数据,如长度的数据有:课桌的高度约为80 cm,中学生拳头的宽度在10 cm左右;中学生一拃的长度约为18 cm;成年人的身高在170 cm左右,一步的步幅在60 cm左右,一层楼的高度在3 m左右等;时间的数据有:一堂课的时间,课间时间,普通中学生跑100 m所用的时间,呼吸一次的时间,眨眼一次的时间等。
类型三 液体和固体的体积测量
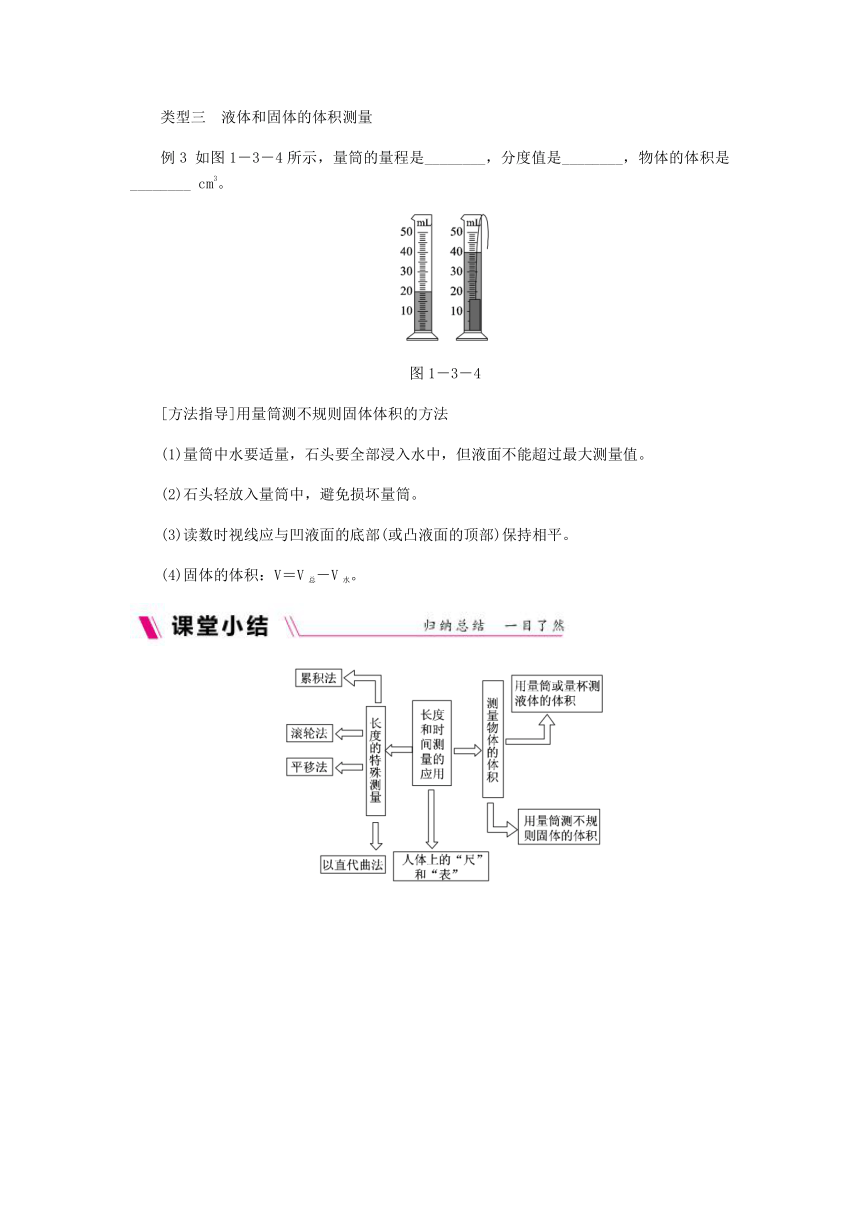
例3 如图1-3-4所示,量筒的量程是________,分度值是________,物体的体积是________ cm3。
图1-3-4
[方法指导]用量筒测不规则固体体积的方法
(1)量筒中水要适量,石头要全部浸入水中,但液面不能超过最大测量值。
(2)石头轻放入量筒中,避免损坏量筒。
(3)读数时视线应与凹液面的底部(或凸液面的顶部)保持相平。
(4)固体的体积:V=V总-V水。
课堂反馈(三)
[长度和时间测量的应用]
1.玲玲用三角板和刻度尺按照图3-1测一角硬币的直径,该刻度尺的分度值是________mm,硬币的直径是________cm。
图3-1
2.某同学用如图3-2所示的方法测量细钢丝的直径;将细钢丝在铅笔上紧密排绕32圈后用刻度尺测量,测得这个线圈的长度是________cm,细钢丝的直径是________mm。
图3-2
3.某学生为测定物理书的纸张厚度,采取如下步骤:
(a)量出这叠纸的厚度L;
(b)选用学生用三角尺,检查零刻度是否磨损;
(c)计算每页纸的厚度d=;
(d)取得物理书内100页叠齐压紧。
上述步骤的正确排列顺序是____________(填字母序号).
上述步骤(c)是错误的,应改为d=________
4.如图3-3所示的量筒,其量程是________mL,分度值是________mL。三名同学在用量筒测液体体积时,读数情况如图所示,其中______同学读数方法正确,量筒中液体体积为________mL。
图3-3
5.下列数据中最接近生活实际的是( )
A.人眨眼一次的时间约5 s B.正常人脉搏每秒跳动70次
C.一个人的身高是165 cm D.一支新铅笔的长度约是15 mm
课时作业(三)
[第一章 1.3 长度和时间测量的应用]
一、选择题
1.一支粉笔的长度最接近( )
A.1 m B.1 dm
C.1 cm D.1 mm
2.人体正常的生命活动中,所用时间最接近1 s的是( )
A.呼吸一次 B.心脏跳动一次
C.打一次哈欠 D.正常步行10 m
3.如图3-K-1所示,用刻度尺测量铅笔的长度,测量方法正确的是( )
图3-K-1
4.要测量如图3-K-2所示的一根曲线MN的长度,你认为可取的方法是( )
图3-K-2
A.用平直的刻度尺在曲线上从起点到终点慢慢移动,直接读出数值
B.用一条细丝线与曲线完全重合,在丝线上标出曲线的起点和终点,把丝线拉直后用刻度尺测出这两点间的距离,即等于曲线的长度
C.用橡皮筋代替细丝线,测量过程同B
D.用三角板量出MN间的距离
5.下列测量长度的方法错误的是( )
A.测一张纸的厚度可以用刻度尺先测出几十张同样纸的厚度,然后再除以纸的总张数,即得出一张纸的厚度
B.测细金属丝的直径,可以把金属丝紧密地单层缠绕在一支铅笔上若干圈,测出密绕部分的长度L和圈数N,则直径为D=
C.测自行车通过的路程,可先记下车轮转过的圈数N,再乘车轮的周长L
D.只使用一个刻度尺不用其他工具就可以准确地测出乒乓球的直径
6.在测量头发丝的直径时,如果把头发丝绕在铅笔上时没有紧密排列,那测量结果将会( )
A.大于真实值 B.小于真实值
C.等于真实值 D.没有影响
7.下列有关量筒的使用说法不正确的是( )
A.量筒的刻度由下往上增大,最下面的刻度为0,且刻度是下密上疏
B.量筒可用来测液体的体积,也可测不规则固体的体积
C.量取过程中必须放平,倒入液体先快后慢,最后用滴管逐滴加到所需的量
D.读数时视线要跟量筒内液体凹液面的最低处保持水平
8.国庆节前,某市工商部门对全市的白酒进行专项检查,某品牌白酒的酒瓶上标有450 mL的字样,而白酒的容量在446~454 mL均为合格,为了一次性测量出一瓶白酒的体积,最好选用下列哪个量筒( )
A.量程是0~100 mL,分度值是1 mL
B.量程是0~500 mL,分度值是1 mL
C.量程是0~1000 mL,分度值是5 mL
D.量程是0~500 mL,分度值是5 mL
9.用量筒测量液体体积时,小明采用俯视读数法,读出液体的体积为32 mL,则此液体的真实体积将( )
A.大于32 mL B.小于32 mL
C.等于32 mL D.都有可能
10.量筒做得细而高,不做成粗而矮的形状,如图3-K-3所示,主要原因是( )
图3-K-3
A.细高的量筒便于操作,也不易因摔倒而打碎
B.细高的量筒可以做出相对较大的底座,增加稳定性
C.细高的量筒与粗矮的量筒比较,单位体积的刻度线间隔较大,能较准确地读数
D.粗矮的量筒中液体较多,需用较厚的玻璃制作,因而不便读数
二、填空题
11.在学校“运用物理技术破案”趣味游戏活动中,小明根据“通常情况下,人站立时身高大约是脚长的7倍”这一常识,可知如图3-K-4中脚印的长度为________cm,“犯罪嫌疑人”的身高约为________m。
图3-K-4
12.一根钢管,已测得管的内直径为7.2 mm;现用三角板和刻度尺量钢管的外直径,读数如图3-K-5所示。由此得钢管外直径是________mm,钢管壁的厚度是________mm。为了减小误差,应________________________________________________________________________
________________________________________________________________________。
图3-K-5
13.为了能较准确地测量出小球的直径,请用做辅助线的方式在图3-K-6中画出测量方法,并读出小球直径为________cm。
图3-K-6
三、实验探究题
14.(1)用量筒测形状不规则固体体积的步骤如下:在量筒中注入适量的水,读出此时水面所对应的示数V1;把固体浸没在盛有适量水的量筒中,读出此时水面所对应的示数V2,则待测固体的体积V=________。
(2)你认为:在上述操作过程中怎样把握注入量筒内水的多少才是“适量”的?
答:________________________________________________________________________
________________________________________________________________________。
15.如图3-K-7所示是利用量筒测量液体和形状不规则物体体积的过程及读数时的几种方法。请仔细观察,回答下列问题:
图3-K-7
(1)该量筒的最大测量值是________,分度值是________。
(2)在观察液体的体积时,其中观察方法正确的是图________,图丙读出的示数会________。
(3)图丁中测出物体的体积是________cm3。
16.如图3-K-8所示为巧测一高度为l的薄瓶的容积的示意图,用刻度尺先测出瓶底直径为d,瓶口向上倒入一定量水,测出水面高度为l1;然后再堵住瓶口,将瓶子倒置测出水面到瓶底的高度为l2,则瓶子的容积约为( )
图3-K-8
A.πd2l B.πd3
C.πd2(l1+l2) D.πd2(l1-l2)
17.因矿石较大,放不进量筒。因此小芳同学用一个烧杯,按如图3-K-9所示的方法来测量矿石的体积,图中所用量筒的量程为________mL,它的分度值为________;矿石的体积为________。
图3-K-9
详解详析
【新知梳理】
一、以直代曲 累积 平移 滚轮
二、1.(1)测量范围 分度值 (3)凹面底部或凸面顶部
2.(1)适量 (3)V2-V1
三、1.1.6 m 0.5 m 0.1 m 1 min 1 min
【应用示例】
例1
线圈长度/cm
线圈圈数/圈
铜线的直径/cm
3.90
32
0.12
[解析] 由图知:刻度尺上1 cm之间有10个小格,所以一个小格代表1 mm,即刻度尺的分度值为1 mm;线圈左端与6.00 cm对齐,右端与9.90 cm对齐,所以线圈的长度为L=9.90 cm-6.00 cm=3.90 cm;线圈一共32圈,n=32,故铜线的直径d=≈0.12 cm。
例2 B [解析] 由图知,国旗的宽度大约是升旗手身高的2倍,升旗手的身高一般在1.8 m左右,所以国旗宽度在3.3 m左右。
例3 0~50 mL 1 mL 20
[解析] 题图所示,量筒的最大测量值是50 mL,即量筒的量程是0~50 mL;量筒每10 mL分10个小格,每小格表示1 mL,即分度值是1 mL;物体的体积等于排开液体的体积:V物=V总-V水=40 mL-20 mL=20 mL=20 cm3。
【课堂反馈】
1.1 1.10
2.4.85 1.5
3.(b)(d)(a)(c)
4.0~100 1 乙 60 5.C
【课时作业】
1.B 2.B 3.C 4.B 5.D 6.A
7.A [解析] 量筒内径是粗细均匀的,所以刻度也是均匀的,故A选项错误,符合题意;量筒可以直接测量液体的体积,也可以间接测量不规则固体的体积,故B选项正确,不符合题意;测量液体体积的过程中,首先将量筒放平,倒入液体先快后慢,最后用滴管逐滴加到所需的量,保证体积的准确,故C选项正确,不符合题意;读取量筒中液体的体积时,视线要跟量筒内液体凹液面的最低处保持水平,不要仰视或俯视,故D选项正确,不符合题意。
8.B
9.B [解析] 在量取32 mL液体时,俯视读数为32 mL,由于在俯视读数时,视线斜向下,视线与筒壁的交点在液面上,所以,读到的数偏大,实际数偏小,则实际小于32 mL。
10.C [解析] 细的量筒横截面积小,对应相同的体积变化,液面高度变化大,即能显示微小的体积变化,测起来更加准确。量筒的示数是均匀的,做得细而高,表示单位体积的刻度线间隔较大,可以更快、更准确地读数。综上所述,只有C选项的说法正确。
11.25.10 1.76
[解析] 刻度尺的分度值为1 mm,由图知脚印长度为25.10 cm,则“犯罪嫌疑人”的身高是25.10 cm×7=175.7 cm≈1.76 m。
12.13.0 2.9 改变位置多测几个数据后再取平均值
13.如图所示 3.10(3.08~3.12合理即可)
14.(1)V2-V1
(2)注入量筒内的水至少能浸没放入其中的待测固体,且待测固体浸没在水中后,液面位置低于量筒的最大测量值
15. (1)100 mL 2 mL (2)乙 偏小 (3)10
16. C [解析] 酒瓶的底面积为S=,
瓶中水的体积:V水=Sl1=,
瓶中空气体积:V空=Sl2=,
酒瓶的容积为:V瓶=V水+V空=+=πd2(l1+l2)。
17.0~200 10 mL 70 cm3
[解析] (1)量筒的最大测量值是200 mL,即量筒的量程是0~200 mL。
(2)量筒每100 mL分为10个小格,每小格代表10 mL,即分度值是10 mL。
(3)根据量筒的读数方法,视线应平视凹液面的最低处,量筒的示数是:B图200 mL,C图130 mL。
(4)矿石在烧杯中时水面达到标记处,而将量筒中的水倒入烧杯后水面也能到标记处,所以从量筒中倒入烧杯中的水的体积就等于矿石的体积。即V石=V总-V剩=200 mL-130 mL=70 mL=70 cm3。
图1-3-1
一 长度测量的特殊方法
测量对象
器材
图示
方法
地图上铁路线、公路线、河流的长度
弹性不大的棉线、刻度尺
________法
纸张、硬币、邮票的厚度,头发丝、铜丝的直径
刻度尺、铅笔
________法
球、硬币的直径
三角板、刻度尺
________法
操场的长度
自行车、细线、刻度尺
________法
二 用量筒或量杯测液体和固体的体积
1.用量筒测液体的体积
(1)使用前:观察量筒的__________和__________。
(2)使用:把液体缓慢倒入量筒。
(3)读数:读数时,视线应与液面的______________________相平。
[说明] 量筒上所标的单位通常是毫升(mL),1 mL=1 cm3=1×10-6 m3 。量筒呈圆柱形,体积与高度成正比,刻度均匀,没有零刻度线。量杯的刻度线分布不均匀(上密下疏)。
2.用量筒测形状不规则小块固体的体积
(1)先在量筒内倒入________的水,读出量筒内水的体积V1。
(2)把形状不规则的物体用细线系好,轻轻放入量筒内(浸没),读出量筒内液面对应的示数V2。
(3)被测物体的体积V=____________。
三 长度和时间的估测
1.记下你身上的“尺”和“表”
尺
身高
一步
一拃
长度
表
脉搏跳动60次
正常呼吸20次
时间
要估测一个物体的长度,首先要对单位长度有具体的感性认识,可以找一些具体物体的长度来帮助认识和记忆。例如,中学生手指甲的厚度约0.5 mm,手指厚度约1 cm,手掌宽度约1 dm等,充分利用这些已知长度,对一些物体的长度进行估测。
2.古代人用日晷、沙漏、滴漏等来测量时间,现实生活中可以用脉搏来估测时间。
类型一 长度的特殊测量
例1 如图1-3-2所示是小明同学利用一根粗细均匀的铅笔、刻度尺来测量细铁丝的直径。请你帮助小明完成下面的表格。
线圈长度/cm
线圈圈数
铜线的直径/cm
32
图1-3-2
[方法指导]长度的特殊测量方法
(1)累积法:把若干个相同的微小量“累积”起来,变得可直接测量,将测出的总量除以累积的个数,便得到微小量。如测量一张纸的厚度等;(2)平移法:借助辅助器材(如三角板、直尺)把不可直接测量的长度“平移”到刻度尺上,从而可直接测出该长度。如测硬币直径等;(3)以直代曲法:把不能直接测量的曲线变为直线,再用刻度尺测量。如测地图上一段距离的长度等;(4)滚轮法:用已知周长的滚轮在较长的曲线上滚动,记下滚过的圈数,再用滚过的圈数乘轮子的周长,就可得到曲线的长度。如汽车、摩托车上的里程表。
类型二 长度和时间的估测
例2 中华人民共和国的国旗为长方形五星红旗,如图1-3-3所示是天安门广场升旗仪式的场景,根据图片提供的信息估测该国旗的宽度,下列数据最接近实际情况的是( )
图1-3-3
A.1.8 m B.3.3 m
C.4.8 m D.5.5 m
[方法指导]熟悉身边数据,估测长度与时间
此类题需要熟悉并利用身边的一些相关数据,如长度的数据有:课桌的高度约为80 cm,中学生拳头的宽度在10 cm左右;中学生一拃的长度约为18 cm;成年人的身高在170 cm左右,一步的步幅在60 cm左右,一层楼的高度在3 m左右等;时间的数据有:一堂课的时间,课间时间,普通中学生跑100 m所用的时间,呼吸一次的时间,眨眼一次的时间等。
类型三 液体和固体的体积测量
例3 如图1-3-4所示,量筒的量程是________,分度值是________,物体的体积是________ cm3。
图1-3-4
[方法指导]用量筒测不规则固体体积的方法
(1)量筒中水要适量,石头要全部浸入水中,但液面不能超过最大测量值。
(2)石头轻放入量筒中,避免损坏量筒。
(3)读数时视线应与凹液面的底部(或凸液面的顶部)保持相平。
(4)固体的体积:V=V总-V水。
课堂反馈(三)
[长度和时间测量的应用]
1.玲玲用三角板和刻度尺按照图3-1测一角硬币的直径,该刻度尺的分度值是________mm,硬币的直径是________cm。
图3-1
2.某同学用如图3-2所示的方法测量细钢丝的直径;将细钢丝在铅笔上紧密排绕32圈后用刻度尺测量,测得这个线圈的长度是________cm,细钢丝的直径是________mm。
图3-2
3.某学生为测定物理书的纸张厚度,采取如下步骤:
(a)量出这叠纸的厚度L;
(b)选用学生用三角尺,检查零刻度是否磨损;
(c)计算每页纸的厚度d=;
(d)取得物理书内100页叠齐压紧。
上述步骤的正确排列顺序是____________(填字母序号).
上述步骤(c)是错误的,应改为d=________
4.如图3-3所示的量筒,其量程是________mL,分度值是________mL。三名同学在用量筒测液体体积时,读数情况如图所示,其中______同学读数方法正确,量筒中液体体积为________mL。
图3-3
5.下列数据中最接近生活实际的是( )
A.人眨眼一次的时间约5 s B.正常人脉搏每秒跳动70次
C.一个人的身高是165 cm D.一支新铅笔的长度约是15 mm
课时作业(三)
[第一章 1.3 长度和时间测量的应用]
一、选择题
1.一支粉笔的长度最接近( )
A.1 m B.1 dm
C.1 cm D.1 mm
2.人体正常的生命活动中,所用时间最接近1 s的是( )
A.呼吸一次 B.心脏跳动一次
C.打一次哈欠 D.正常步行10 m
3.如图3-K-1所示,用刻度尺测量铅笔的长度,测量方法正确的是( )
图3-K-1
4.要测量如图3-K-2所示的一根曲线MN的长度,你认为可取的方法是( )
图3-K-2
A.用平直的刻度尺在曲线上从起点到终点慢慢移动,直接读出数值
B.用一条细丝线与曲线完全重合,在丝线上标出曲线的起点和终点,把丝线拉直后用刻度尺测出这两点间的距离,即等于曲线的长度
C.用橡皮筋代替细丝线,测量过程同B
D.用三角板量出MN间的距离
5.下列测量长度的方法错误的是( )
A.测一张纸的厚度可以用刻度尺先测出几十张同样纸的厚度,然后再除以纸的总张数,即得出一张纸的厚度
B.测细金属丝的直径,可以把金属丝紧密地单层缠绕在一支铅笔上若干圈,测出密绕部分的长度L和圈数N,则直径为D=
C.测自行车通过的路程,可先记下车轮转过的圈数N,再乘车轮的周长L
D.只使用一个刻度尺不用其他工具就可以准确地测出乒乓球的直径
6.在测量头发丝的直径时,如果把头发丝绕在铅笔上时没有紧密排列,那测量结果将会( )
A.大于真实值 B.小于真实值
C.等于真实值 D.没有影响
7.下列有关量筒的使用说法不正确的是( )
A.量筒的刻度由下往上增大,最下面的刻度为0,且刻度是下密上疏
B.量筒可用来测液体的体积,也可测不规则固体的体积
C.量取过程中必须放平,倒入液体先快后慢,最后用滴管逐滴加到所需的量
D.读数时视线要跟量筒内液体凹液面的最低处保持水平
8.国庆节前,某市工商部门对全市的白酒进行专项检查,某品牌白酒的酒瓶上标有450 mL的字样,而白酒的容量在446~454 mL均为合格,为了一次性测量出一瓶白酒的体积,最好选用下列哪个量筒( )
A.量程是0~100 mL,分度值是1 mL
B.量程是0~500 mL,分度值是1 mL
C.量程是0~1000 mL,分度值是5 mL
D.量程是0~500 mL,分度值是5 mL
9.用量筒测量液体体积时,小明采用俯视读数法,读出液体的体积为32 mL,则此液体的真实体积将( )
A.大于32 mL B.小于32 mL
C.等于32 mL D.都有可能
10.量筒做得细而高,不做成粗而矮的形状,如图3-K-3所示,主要原因是( )
图3-K-3
A.细高的量筒便于操作,也不易因摔倒而打碎
B.细高的量筒可以做出相对较大的底座,增加稳定性
C.细高的量筒与粗矮的量筒比较,单位体积的刻度线间隔较大,能较准确地读数
D.粗矮的量筒中液体较多,需用较厚的玻璃制作,因而不便读数
二、填空题
11.在学校“运用物理技术破案”趣味游戏活动中,小明根据“通常情况下,人站立时身高大约是脚长的7倍”这一常识,可知如图3-K-4中脚印的长度为________cm,“犯罪嫌疑人”的身高约为________m。
图3-K-4
12.一根钢管,已测得管的内直径为7.2 mm;现用三角板和刻度尺量钢管的外直径,读数如图3-K-5所示。由此得钢管外直径是________mm,钢管壁的厚度是________mm。为了减小误差,应________________________________________________________________________
________________________________________________________________________。
图3-K-5
13.为了能较准确地测量出小球的直径,请用做辅助线的方式在图3-K-6中画出测量方法,并读出小球直径为________cm。
图3-K-6
三、实验探究题
14.(1)用量筒测形状不规则固体体积的步骤如下:在量筒中注入适量的水,读出此时水面所对应的示数V1;把固体浸没在盛有适量水的量筒中,读出此时水面所对应的示数V2,则待测固体的体积V=________。
(2)你认为:在上述操作过程中怎样把握注入量筒内水的多少才是“适量”的?
答:________________________________________________________________________
________________________________________________________________________。
15.如图3-K-7所示是利用量筒测量液体和形状不规则物体体积的过程及读数时的几种方法。请仔细观察,回答下列问题:
图3-K-7
(1)该量筒的最大测量值是________,分度值是________。
(2)在观察液体的体积时,其中观察方法正确的是图________,图丙读出的示数会________。
(3)图丁中测出物体的体积是________cm3。
16.如图3-K-8所示为巧测一高度为l的薄瓶的容积的示意图,用刻度尺先测出瓶底直径为d,瓶口向上倒入一定量水,测出水面高度为l1;然后再堵住瓶口,将瓶子倒置测出水面到瓶底的高度为l2,则瓶子的容积约为( )
图3-K-8
A.πd2l B.πd3
C.πd2(l1+l2) D.πd2(l1-l2)
17.因矿石较大,放不进量筒。因此小芳同学用一个烧杯,按如图3-K-9所示的方法来测量矿石的体积,图中所用量筒的量程为________mL,它的分度值为________;矿石的体积为________。
图3-K-9
详解详析
【新知梳理】
一、以直代曲 累积 平移 滚轮
二、1.(1)测量范围 分度值 (3)凹面底部或凸面顶部
2.(1)适量 (3)V2-V1
三、1.1.6 m 0.5 m 0.1 m 1 min 1 min
【应用示例】
例1
线圈长度/cm
线圈圈数/圈
铜线的直径/cm
3.90
32
0.12
[解析] 由图知:刻度尺上1 cm之间有10个小格,所以一个小格代表1 mm,即刻度尺的分度值为1 mm;线圈左端与6.00 cm对齐,右端与9.90 cm对齐,所以线圈的长度为L=9.90 cm-6.00 cm=3.90 cm;线圈一共32圈,n=32,故铜线的直径d=≈0.12 cm。
例2 B [解析] 由图知,国旗的宽度大约是升旗手身高的2倍,升旗手的身高一般在1.8 m左右,所以国旗宽度在3.3 m左右。
例3 0~50 mL 1 mL 20
[解析] 题图所示,量筒的最大测量值是50 mL,即量筒的量程是0~50 mL;量筒每10 mL分10个小格,每小格表示1 mL,即分度值是1 mL;物体的体积等于排开液体的体积:V物=V总-V水=40 mL-20 mL=20 mL=20 cm3。
【课堂反馈】
1.1 1.10
2.4.85 1.5
3.(b)(d)(a)(c)
4.0~100 1 乙 60 5.C
【课时作业】
1.B 2.B 3.C 4.B 5.D 6.A
7.A [解析] 量筒内径是粗细均匀的,所以刻度也是均匀的,故A选项错误,符合题意;量筒可以直接测量液体的体积,也可以间接测量不规则固体的体积,故B选项正确,不符合题意;测量液体体积的过程中,首先将量筒放平,倒入液体先快后慢,最后用滴管逐滴加到所需的量,保证体积的准确,故C选项正确,不符合题意;读取量筒中液体的体积时,视线要跟量筒内液体凹液面的最低处保持水平,不要仰视或俯视,故D选项正确,不符合题意。
8.B
9.B [解析] 在量取32 mL液体时,俯视读数为32 mL,由于在俯视读数时,视线斜向下,视线与筒壁的交点在液面上,所以,读到的数偏大,实际数偏小,则实际小于32 mL。
10.C [解析] 细的量筒横截面积小,对应相同的体积变化,液面高度变化大,即能显示微小的体积变化,测起来更加准确。量筒的示数是均匀的,做得细而高,表示单位体积的刻度线间隔较大,可以更快、更准确地读数。综上所述,只有C选项的说法正确。
11.25.10 1.76
[解析] 刻度尺的分度值为1 mm,由图知脚印长度为25.10 cm,则“犯罪嫌疑人”的身高是25.10 cm×7=175.7 cm≈1.76 m。
12.13.0 2.9 改变位置多测几个数据后再取平均值
13.如图所示 3.10(3.08~3.12合理即可)
14.(1)V2-V1
(2)注入量筒内的水至少能浸没放入其中的待测固体,且待测固体浸没在水中后,液面位置低于量筒的最大测量值
15. (1)100 mL 2 mL (2)乙 偏小 (3)10
16. C [解析] 酒瓶的底面积为S=,
瓶中水的体积:V水=Sl1=,
瓶中空气体积:V空=Sl2=,
酒瓶的容积为:V瓶=V水+V空=+=πd2(l1+l2)。
17.0~200 10 mL 70 cm3
[解析] (1)量筒的最大测量值是200 mL,即量筒的量程是0~200 mL。
(2)量筒每100 mL分为10个小格,每小格代表10 mL,即分度值是10 mL。
(3)根据量筒的读数方法,视线应平视凹液面的最低处,量筒的示数是:B图200 mL,C图130 mL。
(4)矿石在烧杯中时水面达到标记处,而将量筒中的水倒入烧杯后水面也能到标记处,所以从量筒中倒入烧杯中的水的体积就等于矿石的体积。即V石=V总-V剩=200 mL-130 mL=70 mL=70 cm3。
同课章节目录
- 第一章 走进物理世界
- 1 希望你喜爱物理
- 2 测量长度和时间
- 3 长度和时间测量的应用
- 4 尝试科学探究
- 第二章 声音与环境
- 1 我们怎样听见声音
- 2 我们怎样区分声音
- 3 我们怎样区分声音(续)
- 4 让声音为人类服务
- 第三章 光和眼睛
- 1 光世界巡行
- 2 探究光的反射规律
- 3 探究平面镜成像特点
- 4 探究光的折射规律
- 5 奇妙的透镜
- 6 探究凸透镜成像规律
- 7 眼睛与光学仪器
- 第四章 物质形态及其变化
- 1 从地球变暖谈起
- 2 探究汽化和液化的特点
- 3 探究熔化和凝固的特点
- 4 升华和凝华
- 5 水循环与水资源
- 第五章 我们周围的物质
- 1 物体的质量
- 2 探究物质的密度
- 3 密度的应用
- 4 认识物质的一些物理属性
- 5 点击新材料
