2018_2019高中数学第一章空间几何体章末复习课学案新人教A版必修2
文档属性
| 名称 | 2018_2019高中数学第一章空间几何体章末复习课学案新人教A版必修2 |
|
|
| 格式 | zip | ||
| 文件大小 | 329.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-24 00:00:00 | ||
图片预览


文档简介
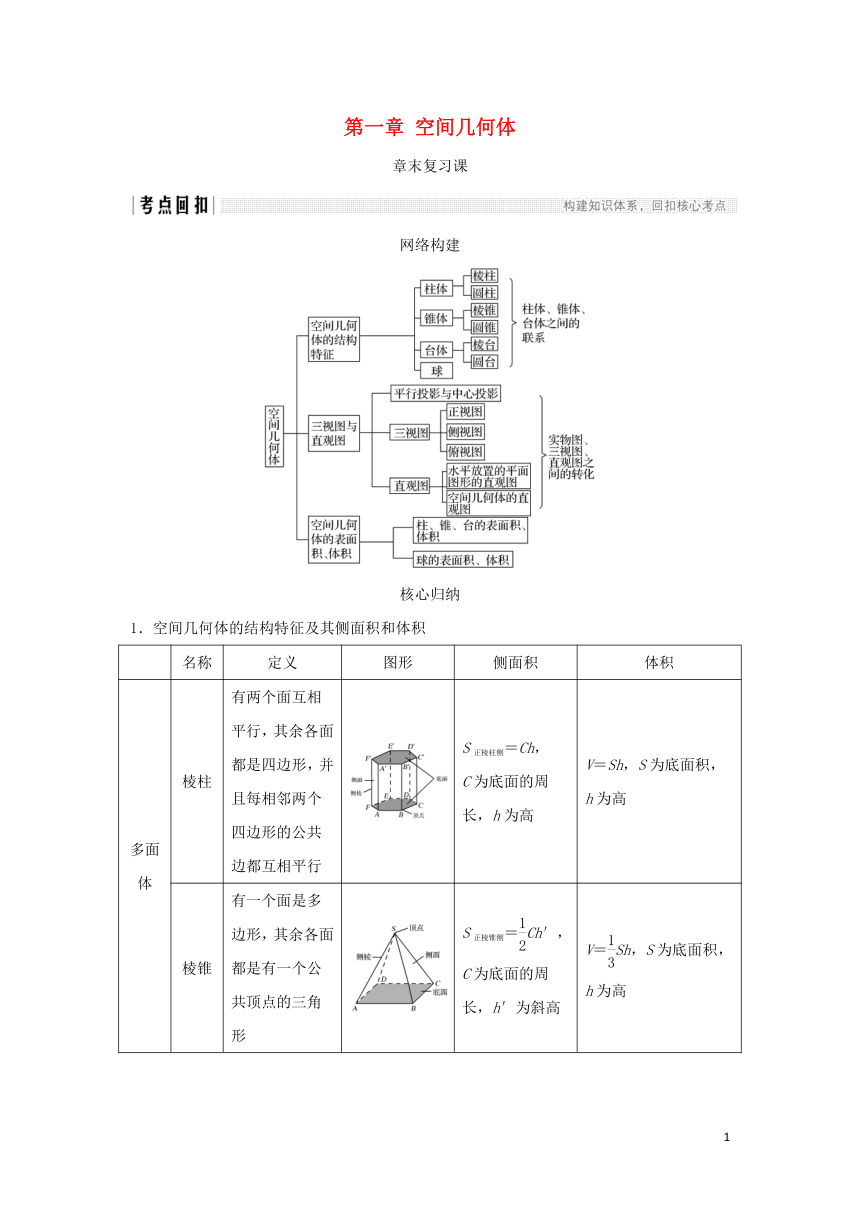
第一章 空间几何体
章末复习课
网络构建
核心归纳
1.空间几何体的结构特征及其侧面积和体积
名称
定义
图形
侧面积
体积
多面体
棱柱
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行
S正棱柱侧=Ch,
C为底面的周长,h为高
V=Sh,S为底面积,
h为高
棱锥
有一个面是多边形,其余各面都是有一个公共顶点的三角形
S正棱锥侧=Ch′,
C为底面的周长,h′为斜高
V=Sh,S为底面积,
h为高
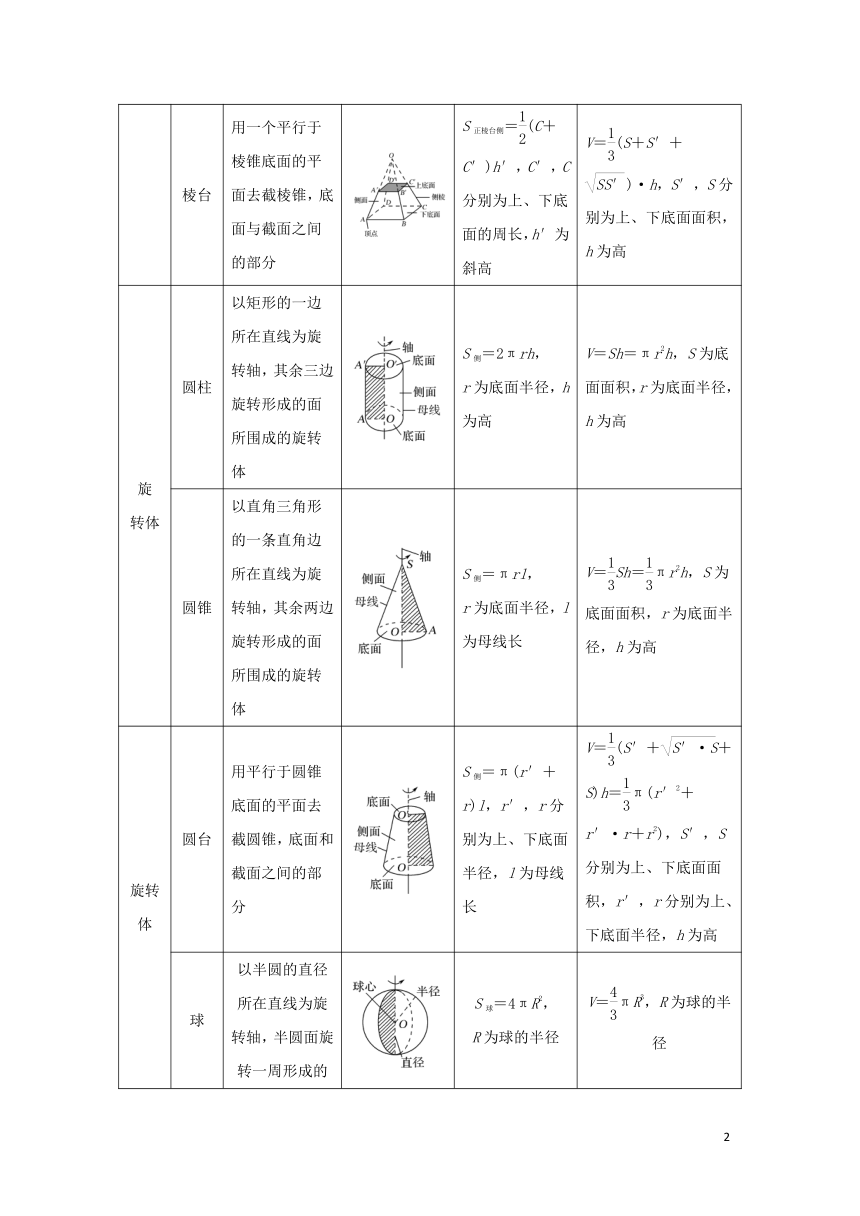
棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分
S正棱台侧=(C+C′)h′,C′,C分别为上、下底面的周长,h′为斜高
V=(S+S′+)·h,S′,S分别为上、下底面面积,h为高
旋
转体
圆柱
以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体
S侧=2πrh,
r为底面半径,h为高
V=Sh=πr2h,S为底面面积,r为底面半径,h为高
圆锥
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体
S侧=πrl,
r为底面半径,l为母线长
V=Sh=πr2h,S为底面面积,r为底面半径,h为高
旋转体
圆台
用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分
S侧=π(r′+r)l,r′,r分别为上、下底面半径,l为母线长
V=(S′++S)h=π(r′2+r′·r+r2),S′,S分别为上、下底面面积,r′,r分别为上、下底面半径,h为高
球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体
S球=4πR2,
R为球的半径
V=πR3,R为球的半径
2.空间几何体的三视图与直观图
(1)三视图是观察者从三个不同位置观察同一个空间几何体而画出的图形;它包括正视图、侧视图、俯视图三种.画图时要遵循“长对正、高平齐、宽相等”的原则,注意三种视图的摆放顺序.在三视图中,分界线和可见轮廓线都用实线画出,不可见轮廓线用虚线画出.熟记常见几何体的三视图.画组合体的三视图时可先拆,后画,再检验.
(2)斜二测画法:主要用于水平放置的平面图形或立体图形的画法.它的主要步骤:
①画轴;②画平行于x、y、z轴的线段分别为平行于x′、y′、z′轴的线段;③截线段:平行于x、z轴的线段的长度不变,平行于y轴的线段的长度变为原来的一半.
三视图和直观图都是空间几何体的不同表示形式,两者之间可以互相转化.
(3)转化思想在本章应用较多,主要体现在以下几个方面
①曲面化平面,如几何体的侧面展开,把曲线(折线)化为线段.
②等积变换,如三棱锥转移顶点等.
③复杂化简单,把不规则几何体通过分割、补体化为规则的几何体等.
要点一 三视图与直观图
解决识图问题,要根据三视图的画法及三视图的特点;解决计算问题,先将三视图还原成直观图,然后再根据有关公式计算.
【例1】 已知一个组合体的三视图如图所示,请根据具体数据来求此几何体的体积(单位:cm).
解 该几何体是由一个圆锥和两个圆柱组合而成的组合体.
由条件中尺寸可知
V圆锥=Sh=π×22×2=π(cm3).
V圆柱中=Sh=π×22×10=40π(cm3),
V圆柱下=Sh=π×62×2=72π(cm3).
∴此组合体的体积V=V圆锥+V圆柱中+V圆柱下
=π+40π+72π=π(cm3).
【训练1】 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
解析 由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,∴在轴截面中圆锥的母线长是=4,∴圆锥的侧面积是π×2×4=8π.下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π,∴空间组合体的表面积是28π,故选C.
答案 C
要点二 空间几何体表面上的最短距离问题
一般地,多面体或旋转体绕侧面或表面最短距离的问题,除球外,基本都是通过展开图来解决,关键是找准剪开的线,准确用展开图中的某条线段来表示这个最短距离,另外这里的所谓最短距离,实质是沿多面体或旋转体侧(表)面的最短路径.
【例2】 边长为5 cm的正方形EFGH是圆柱的轴截面,则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
A.10 cm B.5 cm
C.5 cm D. cm
解析 圆柱的侧面展开图如图所示,展开后E′F=·2π·=π(cm),∴E′G= =
(cm),即为所求最短距离.
答案 D
【训练2】 如图所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,求由A到C1在长方体表面上的最短距离.
解 展开如图①所示,AC1==;
展开如图②所示,AC1==3;
展开如图③所示,AC1==2.
综上,由A到C1在长方体表面上的最短距离为3.
要点三 空间几何体的表面积和体积
1.几何体的表面积及体积的计算是现实生活中经常能够遇到的问题,在计算中应注意各数量之间的关系及各元素之间的位置关系,特别是特殊的柱、锥、台,要注意其中矩形、梯形及直角三角形等重要的平面图形的作用.
2.常见的计算方法
(1)公式法:根据题意直接套用表面积或体积公式求解.
(2)割补法:割补法的思想是通过分割或补形,将原几何体分割成或补成较易计算体积的几何体,从而求出原几何体的体积.
(3)等体积变换法:等积变换法的思想是从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理来求原几何体的体积.
【例3】 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则的值是________.
解析 设球半径为R,则圆柱底面圆半径为R,母线长为2R,又V1=πR2·2R=2πR3,V2=πR3,所以==.
答案
【训练3】 已知等边圆柱(轴截面是正方形的圆柱)的表面积为S,求其内接正四棱柱的体积.
解 如图所示,
设圆柱OO1为等边圆柱,正四棱柱ABCD-A1B1C1D1是圆柱OO1的内接正四棱柱.设等边圆柱的底面半径为r,则高h=2r.
∵S=S侧+2S底=2πrh+2πr2=6πr2,∴r=.
又正四棱柱ABCD-A1B1C1D1的底边AB=2rsin 45°=r,
∴正四棱柱ABCD-A1B1C1D1的体积
V=S底·h=(r)2·2r=4r3=4=.
故该圆柱的内接正四棱柱的体积为.
章末复习课
网络构建
核心归纳
1.空间几何体的结构特征及其侧面积和体积
名称
定义
图形
侧面积
体积
多面体
棱柱
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行
S正棱柱侧=Ch,
C为底面的周长,h为高
V=Sh,S为底面积,
h为高
棱锥
有一个面是多边形,其余各面都是有一个公共顶点的三角形
S正棱锥侧=Ch′,
C为底面的周长,h′为斜高
V=Sh,S为底面积,
h为高
棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分
S正棱台侧=(C+C′)h′,C′,C分别为上、下底面的周长,h′为斜高
V=(S+S′+)·h,S′,S分别为上、下底面面积,h为高
旋
转体
圆柱
以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体
S侧=2πrh,
r为底面半径,h为高
V=Sh=πr2h,S为底面面积,r为底面半径,h为高
圆锥
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体
S侧=πrl,
r为底面半径,l为母线长
V=Sh=πr2h,S为底面面积,r为底面半径,h为高
旋转体
圆台
用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分
S侧=π(r′+r)l,r′,r分别为上、下底面半径,l为母线长
V=(S′++S)h=π(r′2+r′·r+r2),S′,S分别为上、下底面面积,r′,r分别为上、下底面半径,h为高
球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体
S球=4πR2,
R为球的半径
V=πR3,R为球的半径
2.空间几何体的三视图与直观图
(1)三视图是观察者从三个不同位置观察同一个空间几何体而画出的图形;它包括正视图、侧视图、俯视图三种.画图时要遵循“长对正、高平齐、宽相等”的原则,注意三种视图的摆放顺序.在三视图中,分界线和可见轮廓线都用实线画出,不可见轮廓线用虚线画出.熟记常见几何体的三视图.画组合体的三视图时可先拆,后画,再检验.
(2)斜二测画法:主要用于水平放置的平面图形或立体图形的画法.它的主要步骤:
①画轴;②画平行于x、y、z轴的线段分别为平行于x′、y′、z′轴的线段;③截线段:平行于x、z轴的线段的长度不变,平行于y轴的线段的长度变为原来的一半.
三视图和直观图都是空间几何体的不同表示形式,两者之间可以互相转化.
(3)转化思想在本章应用较多,主要体现在以下几个方面
①曲面化平面,如几何体的侧面展开,把曲线(折线)化为线段.
②等积变换,如三棱锥转移顶点等.
③复杂化简单,把不规则几何体通过分割、补体化为规则的几何体等.
要点一 三视图与直观图
解决识图问题,要根据三视图的画法及三视图的特点;解决计算问题,先将三视图还原成直观图,然后再根据有关公式计算.
【例1】 已知一个组合体的三视图如图所示,请根据具体数据来求此几何体的体积(单位:cm).
解 该几何体是由一个圆锥和两个圆柱组合而成的组合体.
由条件中尺寸可知
V圆锥=Sh=π×22×2=π(cm3).
V圆柱中=Sh=π×22×10=40π(cm3),
V圆柱下=Sh=π×62×2=72π(cm3).
∴此组合体的体积V=V圆锥+V圆柱中+V圆柱下
=π+40π+72π=π(cm3).
【训练1】 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
解析 由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,∴在轴截面中圆锥的母线长是=4,∴圆锥的侧面积是π×2×4=8π.下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π,∴空间组合体的表面积是28π,故选C.
答案 C
要点二 空间几何体表面上的最短距离问题
一般地,多面体或旋转体绕侧面或表面最短距离的问题,除球外,基本都是通过展开图来解决,关键是找准剪开的线,准确用展开图中的某条线段来表示这个最短距离,另外这里的所谓最短距离,实质是沿多面体或旋转体侧(表)面的最短路径.
【例2】 边长为5 cm的正方形EFGH是圆柱的轴截面,则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
A.10 cm B.5 cm
C.5 cm D. cm
解析 圆柱的侧面展开图如图所示,展开后E′F=·2π·=π(cm),∴E′G= =
(cm),即为所求最短距离.
答案 D
【训练2】 如图所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,求由A到C1在长方体表面上的最短距离.
解 展开如图①所示,AC1==;
展开如图②所示,AC1==3;
展开如图③所示,AC1==2.
综上,由A到C1在长方体表面上的最短距离为3.
要点三 空间几何体的表面积和体积
1.几何体的表面积及体积的计算是现实生活中经常能够遇到的问题,在计算中应注意各数量之间的关系及各元素之间的位置关系,特别是特殊的柱、锥、台,要注意其中矩形、梯形及直角三角形等重要的平面图形的作用.
2.常见的计算方法
(1)公式法:根据题意直接套用表面积或体积公式求解.
(2)割补法:割补法的思想是通过分割或补形,将原几何体分割成或补成较易计算体积的几何体,从而求出原几何体的体积.
(3)等体积变换法:等积变换法的思想是从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理来求原几何体的体积.
【例3】 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则的值是________.
解析 设球半径为R,则圆柱底面圆半径为R,母线长为2R,又V1=πR2·2R=2πR3,V2=πR3,所以==.
答案
【训练3】 已知等边圆柱(轴截面是正方形的圆柱)的表面积为S,求其内接正四棱柱的体积.
解 如图所示,
设圆柱OO1为等边圆柱,正四棱柱ABCD-A1B1C1D1是圆柱OO1的内接正四棱柱.设等边圆柱的底面半径为r,则高h=2r.
∵S=S侧+2S底=2πrh+2πr2=6πr2,∴r=.
又正四棱柱ABCD-A1B1C1D1的底边AB=2rsin 45°=r,
∴正四棱柱ABCD-A1B1C1D1的体积
V=S底·h=(r)2·2r=4r3=4=.
故该圆柱的内接正四棱柱的体积为.
