2018_2019高中数学第一章空间几何体章末检测新人教A版必修2
文档属性
| 名称 | 2018_2019高中数学第一章空间几何体章末检测新人教A版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-24 00:00:00 | ||
图片预览



文档简介
第一章 空间几何体
章末检测(一)
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分)
1.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧视图为( )
解析 观察所给几何体知侧视图应该是一个正方形,所以D错;中间的棱在侧视图中应该为正方形的从左上到右下的一条对角线,所以A,C错,故B选项正确.
答案 B
2.一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;②正方形;③圆.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
解析 根据画三视图的规则“长对正,高平齐,宽相等”可知,几何体的俯视图不可能是圆和正方形.
答案 B
3.如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )
A. B.1 C. D.2
解析 ∵Rt△O′A′B是一平面图形的直观图,斜边O′B′=2,
∴Rt△O′A′B的直角边长是,
∴Rt△O′A′B的面积是××=1,
∴原平面图形的面积是1×2=2.故选D.
答案 D
4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
A.18+36 B.54+18
C.90 D.81
解析 由已知中的三视图可得:该几何体是一个以边长为3的正方形为底面的斜四棱柱,
其底面面积为:3×3×2=18,
前后侧面的面积为:3×6×2=36,
左右侧面的面积为:3××2=18,
故棱柱的表面积为:18+36+18=54+18.故选B.
答案 B
5.某多面体的三视图如图所示,其中正视图和侧视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A.10 B.12 C.14 D.16
解析 由三视图可画出直观图,该直观图各面内只有两个相同的梯形的面,S梯=(2+4)×2÷2=6,S全梯=6×2=12,故选B.
答案 B
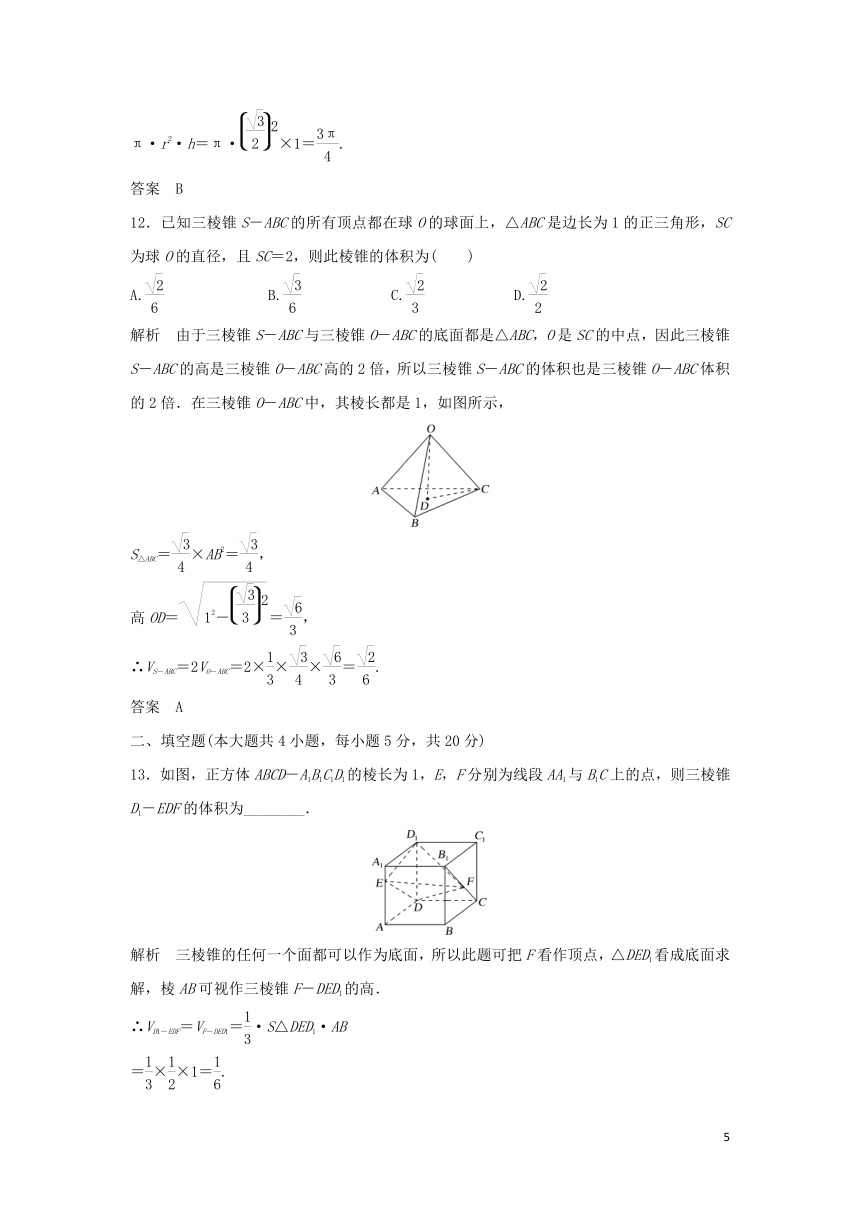
6.如图所示的正方体中,M,N分别是AA1,CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
解析 四边形D1MBN在上、下底面的正投影为A;在前、后面上的正投影为B;在左、右面上的正投影为C;故答案为D.
答案 D
7.若在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面去截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( )
A. B. C. D.
解析 易知V=1-8×××××=.
答案 D
8.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A.60 B.30 C.20 D.10
解析 由三视图知可把三棱锥放在一个长方体内部,即三棱锥A1-BCD,
VA1-BCD=××3×5×4=10,故选D.
答案 D
9.圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A.120° B.150° C.180° D.240°
解析 S底+S侧=3S底,2S底=S侧,即:2πr2=πrl,得2r=l.设侧面展开图的圆心角为θ,则=2πr,∴θ=180°.
答案 C
10.底面半径为,母线长为2的圆锥的外接球O的表面积为( )
A.6π B.12π C.8π D.16π
解析 由题意,圆锥轴截面的顶角为120°,设该圆锥的底面圆心为O′,球O的半径为R,则O′O=R-1,由勾股定理可得R2=(R-1)2+()2,∴R=2,∴球O的表面积为4πR2=16π.故选D.
答案 D
11.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π B. C. D.
解析 如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA=1,球心到底面圆的距离为OM=.
∴底面圆半径r==,故圆柱体积V=
π·r2·h=π·×1=.
答案 B
12.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为( )
A. B. C. D.
解析 由于三棱锥S-ABC与三棱锥O-ABC的底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都是1,如图所示,
S△ABC=×AB2=,
高OD==,
∴VS-ABC=2VO-ABC=2×××=.
答案 A
二、填空题(本大题共4小题,每小题5分,共20分)
13.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1与B1C上的点,则三棱锥D1-EDF的体积为________.
解析 三棱锥的任何一个面都可以作为底面,所以此题可把F看作顶点,△DED1看成底面求解,棱AB可视作三棱锥F-DED1的高.
∴VD1-EDF=VF-DED1=·S△DED1·AB
=××1=.
答案
14.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是________.
解析 ∵圆柱的侧面展开图是边长为1的正方形,
∴该圆柱的高h=1,底面周长2πr=1,
∴底面半径r=,
∴该圆柱的体积V=π··1=.
答案
15.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为________厘米.
解析 V=Sh=πr2h=πR3,R==12(cm).
答案 12
16.直角梯形的一个内角为45°,下底长为上底长的倍,这个梯形绕下底所在直线旋转一周所成的旋转体的表面积为(5+)π,则旋转体的体积为________.
解析 如图所示的是旋转体的半轴截面,设直角梯形的上底长为r,则下底长为
r,∠C=45°,所以DE=,DC=r,所以旋转体的表面积为S表=π·+2π··r+π··r=πr2.
又因为S表=(5+)π,所以r2=4,所以r=2,所以V=π··r+π··=.
答案
三、解答题(本大题共6小题,共70分)
17.(10分)某个几何体的三视图(单位:m)如图所示.
(1)求该几何体的表面积;(结果保留π)
(2)求该几何体的体积.(结果保留π)
解 由三视图可知该几何体的下半部分是棱长为2 m的正方体,上半部分是半径为1 m的半球.
(1)几何体的表面积为
S=×4π×12+6×22-π×12=(24+π)(m2).
(2)几何体的体积为
V=23+×π×13=(8+)(m3).
18.(12分)如果一个几何体的正视图与侧视图都是全等的长方形,边长分别是4 cm与2 cm,如图所示,俯视图是一个边长为4 cm的正方形.
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
解 (1)由题意可知,该几何体是长方体,
底面是正方形,边长是4,高是2,
因此该几何体的表面积是:2×4×4+4×4×2=64(cm2),即几何体的表面积是
64 cm2.
(2)由长方体与球的性质可得,长方体的体对角线是球的直径,记长方体的体对角线长为d,球的半径是r,
d===6(cm),
所以球的半径为r=3(cm).
因此球的体积V=πr3=×27π=36π(cm3),
所以外接球的体积是36π cm3.
19.(12分)如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积.(其中∠BAC=30°)
解 如图所示,
过C作CO1⊥AB于O1.
在半圆中可得∠BCA=90°,
∠BAC=30°,AB=2R,
∴AC=R,CO1=R,
∴V圆锥AO1+V圆锥BO1=π·CO·AO1+π·CO·BO1=π·CO·(AO1+BO1)=π××2R=R3,
又V球=πR3,∴所求几何体的体积V=πR3-R3=πR3.
20.(12分)如图,降水量是指水平地面上单位面积的降水深度,用上口直径为38 cm,底面直径为24 cm,深度为35 cm的圆台形水桶来测量降水量,如果在一次降雨过程中,此桶盛得的雨水高度正好是桶深的,求本次降雨的降水量是多少.(精确到1 mm)
解 由所盛雨水高度正好是桶深的可知,水深为=5(cm),设水面半径为r,如图所示,过点B作BC⊥AC,交水面于点C′,则AC=(38-24)=7(cm).在△ABC中,∵AC∥A′C′,∴=,即=7,所以r=13(cm).
所以,V水=×5×(122+132+12×13)
=(cm3),
S上底=πR2=π·192=361π(cm2),
所以,=≈2.2(cm)=22(mm).
所以,本次降水量约是22 mm.
21.(12分)已知正三棱台(上、下底面是正三角形,上底面的中心在下底面的投影是下底面的中心)的上、下底面边长分别是2 cm与4 cm,侧棱长是 cm,试求该几何体体积.
解 如图,O′,O是上、下底面中心,连接OO′,O′B′,OB,在平面BAA′B′内过B′作B′D⊥BA于点D,在平面BOO′B′内作B′E⊥OB于点E.
∵△A′B′C′是边长为2 cm的等边三角形,O′是△A′B′C′的中心,
∴O′B′=×2×=(cm),
同理OB= cm,则BE=OB-O′B′=(cm).
在Rt△B′EB中,BB′= cm,BE= cm,
∴B′E= cm,即棱台高为 cm.
∴三棱台的体积为
V棱台=××(×16+×4+)=(cm3).
22.(12分)一块边长为10 cm的正方形铁皮按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.
(1)试把容器的容积V表示为x的函数;
(2)若x=6,求图2的正视图的面积.
解 (1)连接AC,BD交于点O,
取BC的中点F,连接EO,OF,EF,
则在Rt△EOF中,EF=5 cm,OF=x cm,
所以EO=.
于是V=x2(cm3).
依题意函数的定义域为{x|0(2)正视图为等腰三角形,腰长为斜高,底边长=AB=6,
底边上的高为四棱锥的高=EO==4,
∴正视图的面积S==12(cm2).
章末检测(一)
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分)
1.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧视图为( )
解析 观察所给几何体知侧视图应该是一个正方形,所以D错;中间的棱在侧视图中应该为正方形的从左上到右下的一条对角线,所以A,C错,故B选项正确.
答案 B
2.一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;②正方形;③圆.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
解析 根据画三视图的规则“长对正,高平齐,宽相等”可知,几何体的俯视图不可能是圆和正方形.
答案 B
3.如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )
A. B.1 C. D.2
解析 ∵Rt△O′A′B是一平面图形的直观图,斜边O′B′=2,
∴Rt△O′A′B的直角边长是,
∴Rt△O′A′B的面积是××=1,
∴原平面图形的面积是1×2=2.故选D.
答案 D
4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
A.18+36 B.54+18
C.90 D.81
解析 由已知中的三视图可得:该几何体是一个以边长为3的正方形为底面的斜四棱柱,
其底面面积为:3×3×2=18,
前后侧面的面积为:3×6×2=36,
左右侧面的面积为:3××2=18,
故棱柱的表面积为:18+36+18=54+18.故选B.
答案 B
5.某多面体的三视图如图所示,其中正视图和侧视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A.10 B.12 C.14 D.16
解析 由三视图可画出直观图,该直观图各面内只有两个相同的梯形的面,S梯=(2+4)×2÷2=6,S全梯=6×2=12,故选B.
答案 B
6.如图所示的正方体中,M,N分别是AA1,CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
解析 四边形D1MBN在上、下底面的正投影为A;在前、后面上的正投影为B;在左、右面上的正投影为C;故答案为D.
答案 D
7.若在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面去截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( )
A. B. C. D.
解析 易知V=1-8×××××=.
答案 D
8.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A.60 B.30 C.20 D.10
解析 由三视图知可把三棱锥放在一个长方体内部,即三棱锥A1-BCD,
VA1-BCD=××3×5×4=10,故选D.
答案 D
9.圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A.120° B.150° C.180° D.240°
解析 S底+S侧=3S底,2S底=S侧,即:2πr2=πrl,得2r=l.设侧面展开图的圆心角为θ,则=2πr,∴θ=180°.
答案 C
10.底面半径为,母线长为2的圆锥的外接球O的表面积为( )
A.6π B.12π C.8π D.16π
解析 由题意,圆锥轴截面的顶角为120°,设该圆锥的底面圆心为O′,球O的半径为R,则O′O=R-1,由勾股定理可得R2=(R-1)2+()2,∴R=2,∴球O的表面积为4πR2=16π.故选D.
答案 D
11.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π B. C. D.
解析 如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA=1,球心到底面圆的距离为OM=.
∴底面圆半径r==,故圆柱体积V=
π·r2·h=π·×1=.
答案 B
12.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为( )
A. B. C. D.
解析 由于三棱锥S-ABC与三棱锥O-ABC的底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都是1,如图所示,
S△ABC=×AB2=,
高OD==,
∴VS-ABC=2VO-ABC=2×××=.
答案 A
二、填空题(本大题共4小题,每小题5分,共20分)
13.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1与B1C上的点,则三棱锥D1-EDF的体积为________.
解析 三棱锥的任何一个面都可以作为底面,所以此题可把F看作顶点,△DED1看成底面求解,棱AB可视作三棱锥F-DED1的高.
∴VD1-EDF=VF-DED1=·S△DED1·AB
=××1=.
答案
14.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是________.
解析 ∵圆柱的侧面展开图是边长为1的正方形,
∴该圆柱的高h=1,底面周长2πr=1,
∴底面半径r=,
∴该圆柱的体积V=π··1=.
答案
15.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为________厘米.
解析 V=Sh=πr2h=πR3,R==12(cm).
答案 12
16.直角梯形的一个内角为45°,下底长为上底长的倍,这个梯形绕下底所在直线旋转一周所成的旋转体的表面积为(5+)π,则旋转体的体积为________.
解析 如图所示的是旋转体的半轴截面,设直角梯形的上底长为r,则下底长为
r,∠C=45°,所以DE=,DC=r,所以旋转体的表面积为S表=π·+2π··r+π··r=πr2.
又因为S表=(5+)π,所以r2=4,所以r=2,所以V=π··r+π··=.
答案
三、解答题(本大题共6小题,共70分)
17.(10分)某个几何体的三视图(单位:m)如图所示.
(1)求该几何体的表面积;(结果保留π)
(2)求该几何体的体积.(结果保留π)
解 由三视图可知该几何体的下半部分是棱长为2 m的正方体,上半部分是半径为1 m的半球.
(1)几何体的表面积为
S=×4π×12+6×22-π×12=(24+π)(m2).
(2)几何体的体积为
V=23+×π×13=(8+)(m3).
18.(12分)如果一个几何体的正视图与侧视图都是全等的长方形,边长分别是4 cm与2 cm,如图所示,俯视图是一个边长为4 cm的正方形.
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
解 (1)由题意可知,该几何体是长方体,
底面是正方形,边长是4,高是2,
因此该几何体的表面积是:2×4×4+4×4×2=64(cm2),即几何体的表面积是
64 cm2.
(2)由长方体与球的性质可得,长方体的体对角线是球的直径,记长方体的体对角线长为d,球的半径是r,
d===6(cm),
所以球的半径为r=3(cm).
因此球的体积V=πr3=×27π=36π(cm3),
所以外接球的体积是36π cm3.
19.(12分)如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积.(其中∠BAC=30°)
解 如图所示,
过C作CO1⊥AB于O1.
在半圆中可得∠BCA=90°,
∠BAC=30°,AB=2R,
∴AC=R,CO1=R,
∴V圆锥AO1+V圆锥BO1=π·CO·AO1+π·CO·BO1=π·CO·(AO1+BO1)=π××2R=R3,
又V球=πR3,∴所求几何体的体积V=πR3-R3=πR3.
20.(12分)如图,降水量是指水平地面上单位面积的降水深度,用上口直径为38 cm,底面直径为24 cm,深度为35 cm的圆台形水桶来测量降水量,如果在一次降雨过程中,此桶盛得的雨水高度正好是桶深的,求本次降雨的降水量是多少.(精确到1 mm)
解 由所盛雨水高度正好是桶深的可知,水深为=5(cm),设水面半径为r,如图所示,过点B作BC⊥AC,交水面于点C′,则AC=(38-24)=7(cm).在△ABC中,∵AC∥A′C′,∴=,即=7,所以r=13(cm).
所以,V水=×5×(122+132+12×13)
=(cm3),
S上底=πR2=π·192=361π(cm2),
所以,=≈2.2(cm)=22(mm).
所以,本次降水量约是22 mm.
21.(12分)已知正三棱台(上、下底面是正三角形,上底面的中心在下底面的投影是下底面的中心)的上、下底面边长分别是2 cm与4 cm,侧棱长是 cm,试求该几何体体积.
解 如图,O′,O是上、下底面中心,连接OO′,O′B′,OB,在平面BAA′B′内过B′作B′D⊥BA于点D,在平面BOO′B′内作B′E⊥OB于点E.
∵△A′B′C′是边长为2 cm的等边三角形,O′是△A′B′C′的中心,
∴O′B′=×2×=(cm),
同理OB= cm,则BE=OB-O′B′=(cm).
在Rt△B′EB中,BB′= cm,BE= cm,
∴B′E= cm,即棱台高为 cm.
∴三棱台的体积为
V棱台=××(×16+×4+)=(cm3).
22.(12分)一块边长为10 cm的正方形铁皮按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.
(1)试把容器的容积V表示为x的函数;
(2)若x=6,求图2的正视图的面积.
解 (1)连接AC,BD交于点O,
取BC的中点F,连接EO,OF,EF,
则在Rt△EOF中,EF=5 cm,OF=x cm,
所以EO=.
于是V=x2(cm3).
依题意函数的定义域为{x|0
底边上的高为四棱锥的高=EO==4,
∴正视图的面积S==12(cm2).
