人教版八年级上册各章节压轴题解析:整式的乘法与因式分解
文档属性
| 名称 | 人教版八年级上册各章节压轴题解析:整式的乘法与因式分解 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-24 00:00:00 | ||
图片预览





文档简介
整式的乘法与因式分解
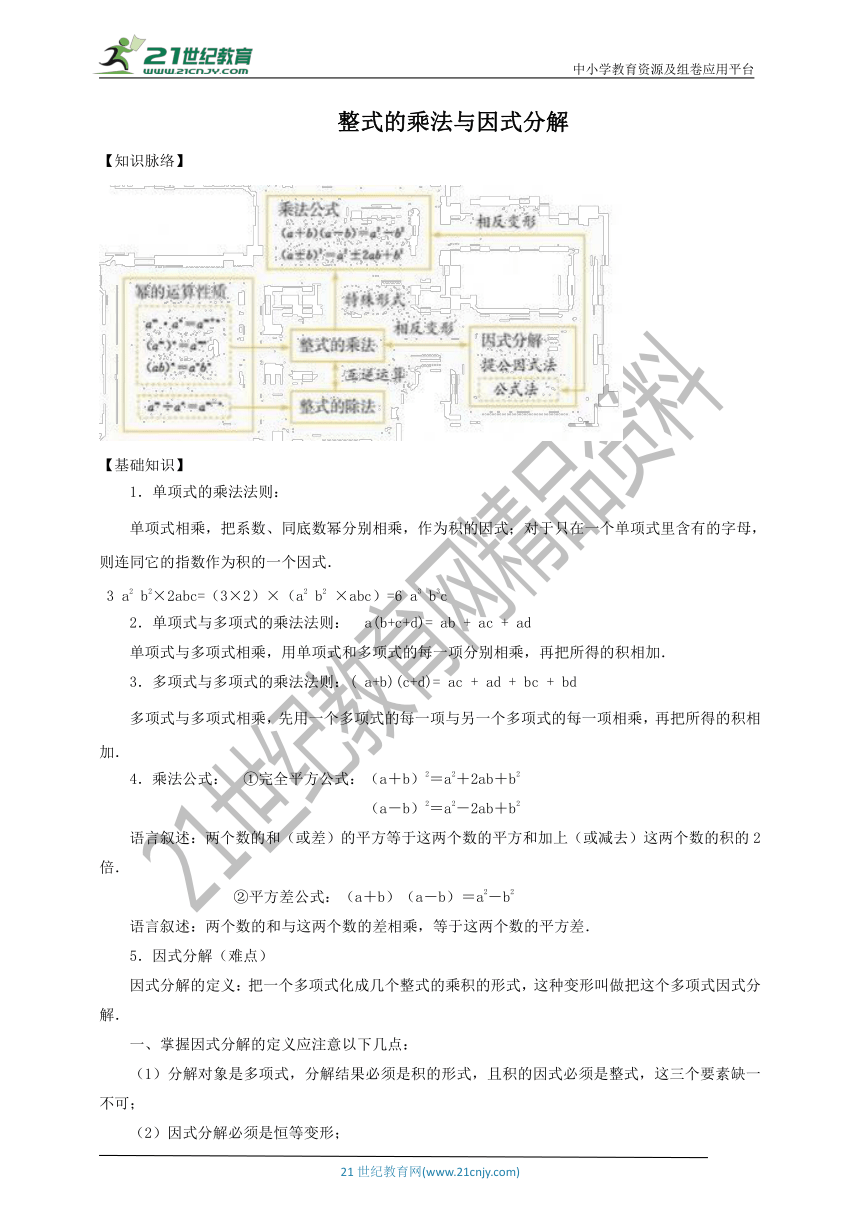
【知识脉络】
【基础知识】
1.单项式的乘法法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
3 a2 b2×2abc=(3×2)×(a2 b2 ×abc)=6 a3 b3c
2.单项式与多项式的乘法法则: a(b+c+d)= ab + ac + ad
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
3.多项式与多项式的乘法法则:( a+b)(c+d)= ac + ad + bc + bd
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
4.乘法公式: ①完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
语言叙述:两个数的和(或差)的平方等于这两个数的平方和加上(或减去)这两个数的积的2倍.
②平方差公式:(a+b)(a-b)=a2-b2
语言叙述:两个数的和与这两个数的差相乘,等于这两个数的平方差.
5.因式分解(难点)
因式分解的定义:把一个多项式化成几个整式的乘积的形式,这种变形叫做把这个多项式因式分解.
一、掌握因式分解的定义应注意以下几点:
(1)分解对象是多项式,分解结果必须是积的形式,且积的因式必须是整式,这三个要素缺一不可;
(2)因式分解必须是恒等变形;
(3)因式分解必须分解到每个因式都不能分解为止.
因式分解与整式乘法是互逆变形,因式分解是把和差化为积的形式,而整式乘法是把积化为和差的形式.
二、熟练掌握因式分解的常用方法.
1、提公因式法
(1)提公因式法的关键是找出公因式,公因式的构成一般情况下有三部分:①系数一各项系数的最大公约数;②字母——各项含有的相同字母;③指数——相同字母的最低次数;
(2)提公因式法的步骤:第一步是找出公因式;第二步是提取公因式并确定另一因式.需注意的是,提取完公因式后,另一个因式的项数与原多项式的项数一致,这一点可用来检验是否漏项.
(3)注意点:①提取公因式后各因式应该是最简形式,即分解到“底”;②如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的.
2、公式法
运用公式法分解因式的实质是把整式中的乘法公式反过来使用;
①平方差公式: a2-b2= (a+b)(a-b)
②完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
【典例解析】
例题1:数学家发明了一个魔术盒,当任意数对(a,b)进入其中时,会得到一个新的数:(a﹣1)(b﹣2).现将数对(m,1)放入其中,得到数n,再将数对(n,m)放入其中后,最后得到的数是 ﹣m2+2m .(结果要化简)
【考点】整式的混合运算.
【分析】根据题意的新定义列出关系式,计算即可得到结果.
【解答】解:根据题意得:(m﹣1)(1﹣2)=n,即n=1﹣m,
则将数对(n,m)代入得:(n﹣1)(m﹣2)=(1﹣m﹣1)(m﹣2)=﹣m2+2m.
故答案为:﹣m2+2m
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
例题2:乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 a2﹣b2 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 a+b ,宽是 a﹣b ,面积是 (a+b)(a﹣b) (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式(两个)
公式1: (a+b)(a﹣b)=a2﹣b2
公式2: a2﹣b2=(a+b)(a﹣b)
(4)运用你所得到的公式计算:10.3×9.7.
【考点】平方差公式的几何背景.
【分析】(1)中的面积=大正方形的面积﹣小正方形的面积=a2﹣b2;
(2)中的长方形,宽为a﹣b,长为a+b,面积=长×宽=(a+b)(a﹣b);
(3)中的答案可以由(1)、(2)得到(a+b)(a﹣b)=a2﹣b2;反过来也成立;
(4)把10.3×9.7写成(10+0.3)(10﹣0.3),利用公式求解即可.
【解答】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2;
(2)长方形的宽为a﹣b,长为a+b,面积=长×宽=(a+b)(a﹣b);
故答案为:a+b,a﹣b,(a+b)(a﹣b);
(3)由(1)、(2)得到,公式1:(a+b)(a﹣b)=a2﹣b2;
公式2:a2﹣b2=(a+b)(a﹣b)
故答案为:(a+b)(a﹣b),a2﹣b2=(a+b)(a﹣b);
(4)10.3×9.7=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91.
例题3:如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A. b2+(b﹣a)2 B. b2+a2 C.(b+a)2 D. a2+2ab
考点:勾股定理.
分析:先求出AE即DE的长,再根据三角形的面积公式求解即可.
解答:解:∵DE=b﹣a,AE=b,
∴S四边形ABCD=4S△ADE+a2=4××(b﹣a)?b
=b2+(b﹣a)2.
故选:A.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
例题4:如图1,我们在2017年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为10×12﹣4×18=48,再选择其他位置的十字星,可以发现“十字差”仍为48.
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 24 .
(2)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
(3)如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2017,则这个十字星中心的数为 975 (直接写出结果).
【考点】规律型:数字的变化类.
【分析】(1)根据题意求出相应的“十字差”,即可确定出所求定值;
(2)定值为k2﹣1=(k+1)(k﹣1),理由为:设十字星中心的数为x,表示出十字星左右两数,上下两数,进而表示出十字差,化简即可得证;
(3)设正中间的数为a,则上下两个数为a﹣62,a+64,左右两个数为a﹣1,a+1,根据相应的“十字差”为2017求出a的值即可.
【解答】解:(1)根据题意得:6×8﹣2×12=48﹣24=24;
故答案为:24;
(2)定值为k2﹣1=(k+1)(k﹣1);
证明:设十字星中心的数为x,则十字星左右两数分别为x﹣1,x+1,上下两数分别为x﹣k,x+k(k≥3),
十字差为(x﹣1)(x+1)﹣(x﹣k)(x+k)=x2﹣1﹣x2+k2=k2﹣1,
故这个定值为k2﹣1=(k+1)(k﹣1);
(3)设正中间的数为a,则上下两个数为a﹣62,a+64,左右两个数为a﹣1,a+1,
根据题意得:(a﹣1)(a+1)﹣(a﹣62)(a+64)=2017,
解得:a=975.
故答案为:975.
【跟踪训练】
1. 利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 .
2. 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
3. 已知a、b、c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.等边三角形
4. 在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减 请你按照这个算法完成下列计算,并回答以下问题
[2016年1月份的日历]
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1)计算:(12+92)﹣(22+82)= ,自己任选一个有4个数的方框进行计算
(2)通过计算你发现什么规律,并说明理由.
5. 已知(x+y)2=25,xy=,求x﹣y的值.
6. 已知,则(a+b)2﹣(a﹣b)2的值为 .
7. ①一个多项式除以2m得1﹣m+m2,这个多项式为 .
② ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 ;若小丽报的是9a2b,则小玉报的整式是 .
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 m.
8. 阅读下面的解答过程,求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,
∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
参考答案:
1. 利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 a2+2ab+b2=(a+b)2 .
【考点】因式分解-运用公式法.
【分析】根据提示可知1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形,利用面积和列出等式即可求解.
【解答】解:两个正方形的面积分别为a2,b2,两个长方形的面积都为ab,组成的正方形的边长为a+b,面积为(a+b)2,
所以a2+2ab+b2=(a+b)2.
【点评】本题考查了运用完全平方公式分解因式,关键是理解题中给出的各个图形之间的面积关系.
2. 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
【考点】多项式乘多项式.
【分析】根据长乘以宽,表示出大长方形的面积,即可确定出三类卡片的张数.
【解答】解:∵(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5ab+2b2,
∴需要A类卡片2张,B类卡片2张,C类卡片5张.
3. 已知a、b、c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.等边三角形
【考点】因式分解的应用.
【分析】已知等式左边分解因式后,利用两数相乘积为0两因式中至少有一个为0得到a=b,即可确定出三角形形状.
【解答】解:已知等式变形得:(a+b)(a﹣b)﹣c(a﹣b)=0,即(a﹣b)(a+b﹣c)=0,
∵a+b﹣c≠0,
∴a﹣b=0,即a=b,
则△ABC为等腰三角形.
故选:C.
4. 在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减 请你按照这个算法完成下列计算,并回答以下问题
[2016年1月份的日历]
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1)计算:(12+92)﹣(22+82)= 14 ,自己任选一个有4个数的方框进行计算 14
(2)通过计算你发现什么规律,并说明理由.
【考点】整式的混合运算.
【分析】(1)先算乘法,再合并即可;
(2)设最小的数字为n,则其余三个分别为n+8,n+1,n+7,根据题意得出算式[n2+(n+8)2]﹣[(n+1)2+(n+7)2],求出即可.
【解答】解:(1)(12+92)﹣(22+82)=1+81﹣4﹣64=14,
(32+112)﹣(42+102)=9+121﹣16﹣100=14,
故答案为:14;
(2)计算结果等于14,
理由是:设最小的数字为n,则其余三个分别为n+8,n+1,n+7,
所以[n2+(n+8)2]﹣[(n+1)2+(n+7)2]
=n2+n2+16n+64﹣n2﹣2n﹣1﹣n2﹣14n﹣49
=14.
5. 已知(x+y)2=25,xy=,求x﹣y的值.
【考点】完全平方公式.
【分析】根据完全平方公式即可求出答案.
【解答】解:∵(x+y)2=x2+2xy+y2,
∴25=x2+y2+,
∴x2+y2=
∵(x﹣y)2=x2﹣2xy+y2,
∴(x﹣y)2=﹣=16
∴x﹣y=±4
6. 已知,则(a+b)2﹣(a﹣b)2的值为 1 .
考点:因式分解-运用公式法.
分析:首先利用完全平方公式展开进而合并同类项,再将已知代入求出即可.
解答:解:∵(a+b)2﹣(a﹣b)2
=(a2+2ab+b2)﹣(a2﹣2ab+b2)
=4ab,
∴将,代入上式可得:
原式=4ab=4××=1.
故答案为:1.
点评:此题主要考查了完全平方公式的应用,熟练掌握完全平方公式的形式是解题关键.
7. ①一个多项式除以2m得1﹣m+m2,这个多项式为 2m﹣2m2+2m3 .
② 6x2+5x﹣6 ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 a﹣b ;若小丽报的是9a2b,则小玉报的整式是 27a3b2 .
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 a+c m.
考点:整式的混合运算.
分析:①利用2m乘1﹣m+m2计算即可;
②把除式和商相乘即可;
③根据被除式÷商=除式,被除式=除式×商列式计算即可;
④利用4块土地换成一块地后的面积与原来4块地的总面积相等,而原来4块地的总面积=a2+bc+ac+ab,得到4块土地换成一块地后面积为(a2+bc+ac+ab)米,又此块地的宽为(a+b)米,根据矩形的面积公式得到此块地的长=(a2+bc+ac+ab)÷(a+b),把被除式分解后再进行除法运算即可得到结论.
解答: 解:①2m(1﹣m+m2)=2m﹣2m2+2m3;
②(2x+3)(3x﹣2)=6x2+5x﹣6;
③(3a2b﹣ab2)÷3ab=a﹣b,
3ab?9a2b=27a3b2;
④∵原来4块地的总面积=a2+bc+ac+ab,
∴将这4块土地换成一块地后面积为(a2+bc+ac+ab)米,
而此块地的宽为(a+b)米,
∴此块地的长=(a2+bc+ac+ab)÷(a+b)
=(a2+ac+bc+ab)÷(a+b)
=[a(a+c)+b(a+c)÷(a+b)]
=(a+b)(a+c)÷(a+b)
=a+c.
故答案为:2m﹣2m2+2m3;6x2+5x﹣6;a﹣b,27a3b2;a+c.
点评: 此题考查整式的混合运算,掌握计算方法是解决问题的关键.
8. 阅读下面的解答过程,求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,
∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
考点:因式分解的应用.
专题:阅读型.
分析:(1)多项式配方后,根据完全平方式恒大于等于0,即可求出最小值;
(2)多项式配方后,根据完全平方式恒大于等于0,即可求出最大值.
解答:解:(1)m2+m+4=(m+)2+,
∵(m+)2≥0,
∴(m+)2+≥.
则m2+m+4的最小值是;
(2)4﹣x2+2x=﹣(x﹣1)2+5,
∵﹣(x﹣1)2≤0,
∴﹣(x﹣1)2+5≤5,
则4﹣x2+2x的最大值为5.
点评:此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.
【知识脉络】
【基础知识】
1.单项式的乘法法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
3 a2 b2×2abc=(3×2)×(a2 b2 ×abc)=6 a3 b3c
2.单项式与多项式的乘法法则: a(b+c+d)= ab + ac + ad
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
3.多项式与多项式的乘法法则:( a+b)(c+d)= ac + ad + bc + bd
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
4.乘法公式: ①完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
语言叙述:两个数的和(或差)的平方等于这两个数的平方和加上(或减去)这两个数的积的2倍.
②平方差公式:(a+b)(a-b)=a2-b2
语言叙述:两个数的和与这两个数的差相乘,等于这两个数的平方差.
5.因式分解(难点)
因式分解的定义:把一个多项式化成几个整式的乘积的形式,这种变形叫做把这个多项式因式分解.
一、掌握因式分解的定义应注意以下几点:
(1)分解对象是多项式,分解结果必须是积的形式,且积的因式必须是整式,这三个要素缺一不可;
(2)因式分解必须是恒等变形;
(3)因式分解必须分解到每个因式都不能分解为止.
因式分解与整式乘法是互逆变形,因式分解是把和差化为积的形式,而整式乘法是把积化为和差的形式.
二、熟练掌握因式分解的常用方法.
1、提公因式法
(1)提公因式法的关键是找出公因式,公因式的构成一般情况下有三部分:①系数一各项系数的最大公约数;②字母——各项含有的相同字母;③指数——相同字母的最低次数;
(2)提公因式法的步骤:第一步是找出公因式;第二步是提取公因式并确定另一因式.需注意的是,提取完公因式后,另一个因式的项数与原多项式的项数一致,这一点可用来检验是否漏项.
(3)注意点:①提取公因式后各因式应该是最简形式,即分解到“底”;②如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的.
2、公式法
运用公式法分解因式的实质是把整式中的乘法公式反过来使用;
①平方差公式: a2-b2= (a+b)(a-b)
②完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
【典例解析】
例题1:数学家发明了一个魔术盒,当任意数对(a,b)进入其中时,会得到一个新的数:(a﹣1)(b﹣2).现将数对(m,1)放入其中,得到数n,再将数对(n,m)放入其中后,最后得到的数是 ﹣m2+2m .(结果要化简)
【考点】整式的混合运算.
【分析】根据题意的新定义列出关系式,计算即可得到结果.
【解答】解:根据题意得:(m﹣1)(1﹣2)=n,即n=1﹣m,
则将数对(n,m)代入得:(n﹣1)(m﹣2)=(1﹣m﹣1)(m﹣2)=﹣m2+2m.
故答案为:﹣m2+2m
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
例题2:乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 a2﹣b2 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 a+b ,宽是 a﹣b ,面积是 (a+b)(a﹣b) (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式(两个)
公式1: (a+b)(a﹣b)=a2﹣b2
公式2: a2﹣b2=(a+b)(a﹣b)
(4)运用你所得到的公式计算:10.3×9.7.
【考点】平方差公式的几何背景.
【分析】(1)中的面积=大正方形的面积﹣小正方形的面积=a2﹣b2;
(2)中的长方形,宽为a﹣b,长为a+b,面积=长×宽=(a+b)(a﹣b);
(3)中的答案可以由(1)、(2)得到(a+b)(a﹣b)=a2﹣b2;反过来也成立;
(4)把10.3×9.7写成(10+0.3)(10﹣0.3),利用公式求解即可.
【解答】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2;
(2)长方形的宽为a﹣b,长为a+b,面积=长×宽=(a+b)(a﹣b);
故答案为:a+b,a﹣b,(a+b)(a﹣b);
(3)由(1)、(2)得到,公式1:(a+b)(a﹣b)=a2﹣b2;
公式2:a2﹣b2=(a+b)(a﹣b)
故答案为:(a+b)(a﹣b),a2﹣b2=(a+b)(a﹣b);
(4)10.3×9.7=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91.
例题3:如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A. b2+(b﹣a)2 B. b2+a2 C.(b+a)2 D. a2+2ab
考点:勾股定理.
分析:先求出AE即DE的长,再根据三角形的面积公式求解即可.
解答:解:∵DE=b﹣a,AE=b,
∴S四边形ABCD=4S△ADE+a2=4××(b﹣a)?b
=b2+(b﹣a)2.
故选:A.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
例题4:如图1,我们在2017年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为10×12﹣4×18=48,再选择其他位置的十字星,可以发现“十字差”仍为48.
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 24 .
(2)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
(3)如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2017,则这个十字星中心的数为 975 (直接写出结果).
【考点】规律型:数字的变化类.
【分析】(1)根据题意求出相应的“十字差”,即可确定出所求定值;
(2)定值为k2﹣1=(k+1)(k﹣1),理由为:设十字星中心的数为x,表示出十字星左右两数,上下两数,进而表示出十字差,化简即可得证;
(3)设正中间的数为a,则上下两个数为a﹣62,a+64,左右两个数为a﹣1,a+1,根据相应的“十字差”为2017求出a的值即可.
【解答】解:(1)根据题意得:6×8﹣2×12=48﹣24=24;
故答案为:24;
(2)定值为k2﹣1=(k+1)(k﹣1);
证明:设十字星中心的数为x,则十字星左右两数分别为x﹣1,x+1,上下两数分别为x﹣k,x+k(k≥3),
十字差为(x﹣1)(x+1)﹣(x﹣k)(x+k)=x2﹣1﹣x2+k2=k2﹣1,
故这个定值为k2﹣1=(k+1)(k﹣1);
(3)设正中间的数为a,则上下两个数为a﹣62,a+64,左右两个数为a﹣1,a+1,
根据题意得:(a﹣1)(a+1)﹣(a﹣62)(a+64)=2017,
解得:a=975.
故答案为:975.
【跟踪训练】
1. 利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 .
2. 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
3. 已知a、b、c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.等边三角形
4. 在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减 请你按照这个算法完成下列计算,并回答以下问题
[2016年1月份的日历]
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1)计算:(12+92)﹣(22+82)= ,自己任选一个有4个数的方框进行计算
(2)通过计算你发现什么规律,并说明理由.
5. 已知(x+y)2=25,xy=,求x﹣y的值.
6. 已知,则(a+b)2﹣(a﹣b)2的值为 .
7. ①一个多项式除以2m得1﹣m+m2,这个多项式为 .
② ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 ;若小丽报的是9a2b,则小玉报的整式是 .
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 m.
8. 阅读下面的解答过程,求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,
∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
参考答案:
1. 利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 a2+2ab+b2=(a+b)2 .
【考点】因式分解-运用公式法.
【分析】根据提示可知1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形,利用面积和列出等式即可求解.
【解答】解:两个正方形的面积分别为a2,b2,两个长方形的面积都为ab,组成的正方形的边长为a+b,面积为(a+b)2,
所以a2+2ab+b2=(a+b)2.
【点评】本题考查了运用完全平方公式分解因式,关键是理解题中给出的各个图形之间的面积关系.
2. 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
【考点】多项式乘多项式.
【分析】根据长乘以宽,表示出大长方形的面积,即可确定出三类卡片的张数.
【解答】解:∵(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5ab+2b2,
∴需要A类卡片2张,B类卡片2张,C类卡片5张.
3. 已知a、b、c是△ABC的三条边,且满足a2+bc=b2+ac,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.等边三角形
【考点】因式分解的应用.
【分析】已知等式左边分解因式后,利用两数相乘积为0两因式中至少有一个为0得到a=b,即可确定出三角形形状.
【解答】解:已知等式变形得:(a+b)(a﹣b)﹣c(a﹣b)=0,即(a﹣b)(a+b﹣c)=0,
∵a+b﹣c≠0,
∴a﹣b=0,即a=b,
则△ABC为等腰三角形.
故选:C.
4. 在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减 请你按照这个算法完成下列计算,并回答以下问题
[2016年1月份的日历]
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1)计算:(12+92)﹣(22+82)= 14 ,自己任选一个有4个数的方框进行计算 14
(2)通过计算你发现什么规律,并说明理由.
【考点】整式的混合运算.
【分析】(1)先算乘法,再合并即可;
(2)设最小的数字为n,则其余三个分别为n+8,n+1,n+7,根据题意得出算式[n2+(n+8)2]﹣[(n+1)2+(n+7)2],求出即可.
【解答】解:(1)(12+92)﹣(22+82)=1+81﹣4﹣64=14,
(32+112)﹣(42+102)=9+121﹣16﹣100=14,
故答案为:14;
(2)计算结果等于14,
理由是:设最小的数字为n,则其余三个分别为n+8,n+1,n+7,
所以[n2+(n+8)2]﹣[(n+1)2+(n+7)2]
=n2+n2+16n+64﹣n2﹣2n﹣1﹣n2﹣14n﹣49
=14.
5. 已知(x+y)2=25,xy=,求x﹣y的值.
【考点】完全平方公式.
【分析】根据完全平方公式即可求出答案.
【解答】解:∵(x+y)2=x2+2xy+y2,
∴25=x2+y2+,
∴x2+y2=
∵(x﹣y)2=x2﹣2xy+y2,
∴(x﹣y)2=﹣=16
∴x﹣y=±4
6. 已知,则(a+b)2﹣(a﹣b)2的值为 1 .
考点:因式分解-运用公式法.
分析:首先利用完全平方公式展开进而合并同类项,再将已知代入求出即可.
解答:解:∵(a+b)2﹣(a﹣b)2
=(a2+2ab+b2)﹣(a2﹣2ab+b2)
=4ab,
∴将,代入上式可得:
原式=4ab=4××=1.
故答案为:1.
点评:此题主要考查了完全平方公式的应用,熟练掌握完全平方公式的形式是解题关键.
7. ①一个多项式除以2m得1﹣m+m2,这个多项式为 2m﹣2m2+2m3 .
② 6x2+5x﹣6 ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 a﹣b ;若小丽报的是9a2b,则小玉报的整式是 27a3b2 .
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 a+c m.
考点:整式的混合运算.
分析:①利用2m乘1﹣m+m2计算即可;
②把除式和商相乘即可;
③根据被除式÷商=除式,被除式=除式×商列式计算即可;
④利用4块土地换成一块地后的面积与原来4块地的总面积相等,而原来4块地的总面积=a2+bc+ac+ab,得到4块土地换成一块地后面积为(a2+bc+ac+ab)米,又此块地的宽为(a+b)米,根据矩形的面积公式得到此块地的长=(a2+bc+ac+ab)÷(a+b),把被除式分解后再进行除法运算即可得到结论.
解答: 解:①2m(1﹣m+m2)=2m﹣2m2+2m3;
②(2x+3)(3x﹣2)=6x2+5x﹣6;
③(3a2b﹣ab2)÷3ab=a﹣b,
3ab?9a2b=27a3b2;
④∵原来4块地的总面积=a2+bc+ac+ab,
∴将这4块土地换成一块地后面积为(a2+bc+ac+ab)米,
而此块地的宽为(a+b)米,
∴此块地的长=(a2+bc+ac+ab)÷(a+b)
=(a2+ac+bc+ab)÷(a+b)
=[a(a+c)+b(a+c)÷(a+b)]
=(a+b)(a+c)÷(a+b)
=a+c.
故答案为:2m﹣2m2+2m3;6x2+5x﹣6;a﹣b,27a3b2;a+c.
点评: 此题考查整式的混合运算,掌握计算方法是解决问题的关键.
8. 阅读下面的解答过程,求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,
∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
考点:因式分解的应用.
专题:阅读型.
分析:(1)多项式配方后,根据完全平方式恒大于等于0,即可求出最小值;
(2)多项式配方后,根据完全平方式恒大于等于0,即可求出最大值.
解答:解:(1)m2+m+4=(m+)2+,
∵(m+)2≥0,
∴(m+)2+≥.
则m2+m+4的最小值是;
(2)4﹣x2+2x=﹣(x﹣1)2+5,
∵﹣(x﹣1)2≤0,
∴﹣(x﹣1)2+5≤5,
则4﹣x2+2x的最大值为5.
点评:此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.
