2018—2019年高中数学第一章立体几何初步章末检测北师大版必修2
文档属性
| 名称 | 2018—2019年高中数学第一章立体几何初步章末检测北师大版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 420.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-25 00:00:00 | ||
图片预览



文档简介
第一章 立体几何初步
章末检测(一)
一、选择题(本大题共12个小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;②若α∥β,β∥γ,m∥α,则m∥γ;③若m∥α,n∥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.① B.②和③
C.③和④ D.①和④
解析 ①正确;②若α∥β,β∥γ,m∥α,则m∥γ或m?γ,②错;③若m∥α,n∥α,则m∥n,而同平行于同一个平面的两条直线有三种位置关系,③错;④垂直于同一个平面的两个平面也可以相交,④错.
答案 A
2.在如右图所示的三棱锥A-BCD中,VA-BPQ=2,VC-APQ=6,VC-DPQ=12,则VA-BCD等于( )
A.20 B.24
C.28 D.56
解析 由==,得=,所以VP-BDQ=VP-CDQ=4,所以VA-BCD=2+6+12+4=24.
答案 B
3.如图,α∩β=l,A、B∈α,C∈β,且C?l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B
C.点C但不过点M D.点C和点M
解析 ∵AB?γ,M∈AB,∴M∈γ.
又α∩β=l,M∈l,∴M∈β.
根据公理3可知,点M在γ与β的交线上.
同理可知,点C也在γ与β的交线上.
答案 D
4.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
解析 如图,设截面圆的圆心为O′,
M为截面圆上任一点,
则OO′=,O′M=1,
∴OM==,
即球的半径为,∴V=π()3=4π.
答案 B
5.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.90° B.60°
C.45° D.30°
解析 连接B′C,则△AB′C为等边三角形,设AD=a,
则B′D=DC=a,B′C=AC=a,
所以∠B′DC=90°.
答案 A
6.如图,平面α⊥平面β,点A∈α,点B∈β,AB与两平面α,β所成的角分别为45°和30°.过点A,B分别作两平面交线的垂线,垂足为A′,B′,若AB=12,则A′B′=( )
A.4 B.6
C.8 D.9
解析 如图所示,连接A′B,AB′,
由题意得BB′⊥α,AA′⊥β,∠BAB′=45°,∠ABA′=30°,BB′⊥A′B′,AA′⊥A′B′,AA′⊥A′B.因为AB=12,所以BA′=AB·cos∠ABA′=6,BB′=ABsin∠BAB′=6,故A′B′==6.
答案 B
7.已知矩形ABCD,AB=1,BC=,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
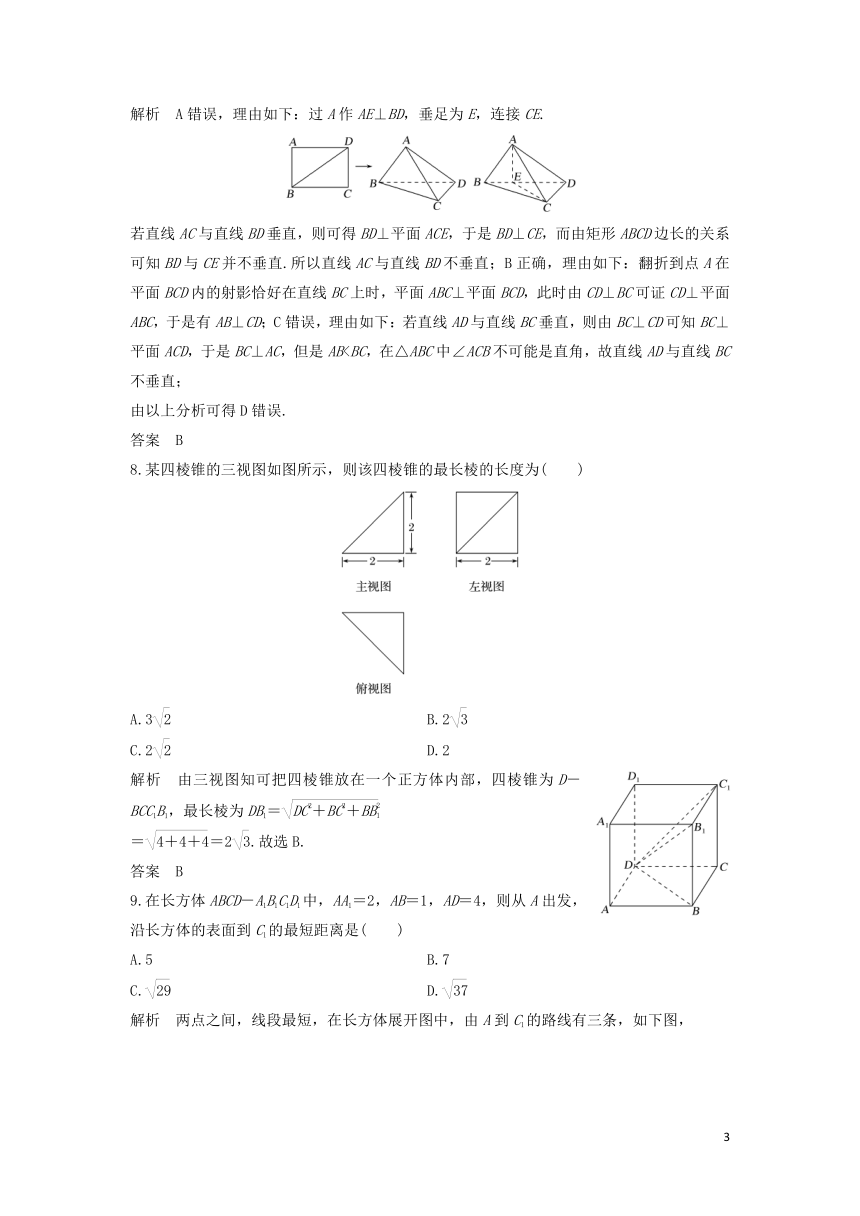
解析 A错误,理由如下:过A作AE⊥BD,垂足为E,连接CE.
若直线AC与直线BD垂直,则可得BD⊥平面ACE,于是BD⊥CE,而由矩形ABCD边长的关系可知BD与CE并不垂直.所以直线AC与直线BD不垂直;B正确,理由如下:翻折到点A在平面BCD内的射影恰好在直线BC上时,平面ABC⊥平面BCD,此时由CD⊥BC可证CD⊥平面ABC,于是有AB⊥CD;C错误,理由如下:若直线AD与直线BC垂直,则由BC⊥CD可知BC⊥平面ACD,于是BC⊥AC,但是AB由以上分析可得D错误.
答案 B
8.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2
C.2 D.2
解析 由三视图知可把四棱锥放在一个正方体内部,四棱锥为D-BCC1B1,最长棱为DB1=
==2.故选B.
答案 B
9.在长方体ABCD-A1B1C1D1中,AA1=2,AB=1,AD=4,则从A出发,沿长方体的表面到C1的最短距离是( )
A.5 B.7
C. D.
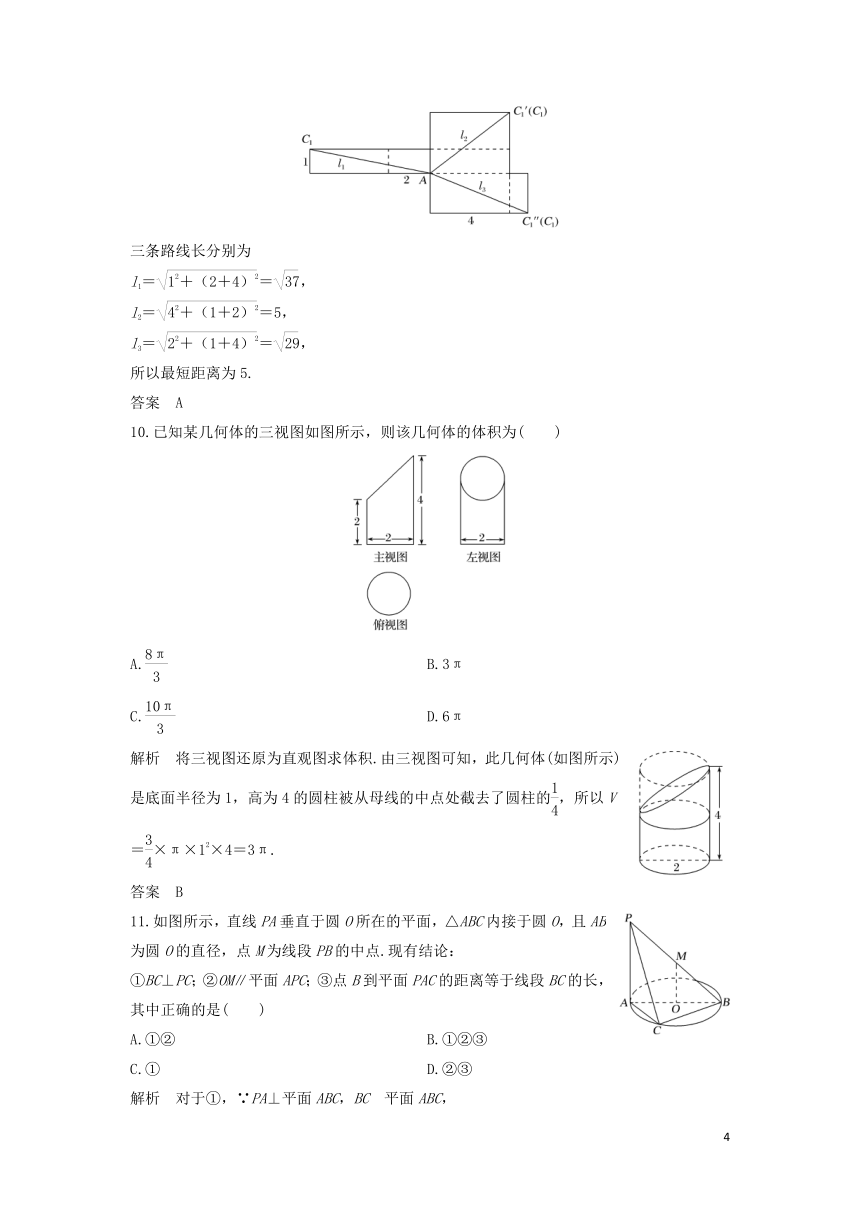
解析 两点之间,线段最短,在长方体展开图中,由A到C1的路线有三条,如下图,
三条路线长分别为
l1==,
l2==5,
l3==,
所以最短距离为5.
答案 A
10.已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B.3π
C. D.6π
解析 将三视图还原为直观图求体积.由三视图可知,此几何体(如图所示)是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的,所以V=×π×12×4=3π.
答案 B
11.如图所示,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有结论:
①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长,其中正确的是( )
A.①② B.①②③
C.① D.②③
解析 对于①,∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
∵AB为圆O的直径,∴BC⊥AC,PA∩AC=A,
∴BC⊥平面PAC,
又PC?平面PAC,∴BC⊥PC,①正确;
对于②,∵点M为线段PB的中点,∴OM∥PA,
∵PA?平面PAC,OM?平面PAC,
∴OM∥平面PAC,②正确;
对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC的距离,故①②③都正确.
答案 B
12.已知二面角α-l-β为60°,动点P,Q分别在平面α,β内,P到β的距离为,Q到α的距离为2,则P,Q两点之间距离的最小值为( )
A. B.2
C.2 D.4
解析 如图,分别作QA⊥α于点A,AC⊥l于点C,PB⊥β于点B,PD⊥l于点D,连接CQ,BD,则∠ACQ=∠PDB=60°,AQ=2,BP=,∴AC=PD=2.又∵PQ==≥2.当且仅当AP=0,即点A与点P重合时取最小值.故选C.
答案 C
二、填空题(本大题共4个小题,每小题5分,共20分)
13.在△ABC中,∠BAC=90°,P为△ABC所在平面外一点,且PA=PB=PC,且平面PBC与平面ABC的位置关系是________.
解析 如右图所示,取BC的中点O,连接AO,PO.
∵PB=PC,∴PO⊥BC.
又△ABC是以A为直角顶点的直角三角形,
∴OA=OB,又PA=PB,
∴△POA≌△POB,
∴∠POA=∠POB=90°,
即PO⊥OA,而OA∩BC=O,
∴PO⊥平面ABC,而PO?平面PBC,
∴平面PBC⊥平面ABC.
答案 垂直
14.已知一个圆锥的展开图如图所示,其中扇形的圆心角为120°,底面圆的半径为1,则该圆锥的体积为________.
解析 因为扇形弧长为2π,设母线长为l,则有×2πl=2π,∴l=3,所以圆锥母线长为3,高为=2,所求体积V=×π×12×2=.
答案
15.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________(写出所有正确结论的编号).
解析 由条件可得AB⊥平面PAD,
∴AB⊥PD,故①正确;
若平面PBC⊥平面ABCD,由PB⊥BC,
得PB⊥平面ABCD,从而PA∥PB,这显然不成立,故②错;
S△PCD=CD·PD,S△PAB=AB·PA,
由AB=CD,PD>PA知③正确;
由E、F分别是棱PC、PD的中点,
可得EF∥CD,又AB∥CD,
∴EF∥AB,故AE与BF共面,故④错.
答案 ①③
16.某三棱锥的三视图如图所示,则该三棱锥的表面积是________.
解析 由三视图可得该三棱锥的直观图如图所示,其中PA=1,BC=2,取BC的中点M,连接AM,MP,则AM=2,AM⊥BC,故AC=AB===,由主视图和左视图可知PA⊥平面ABC,因此可得PC=PB===,PM===,所以三棱锥的表面积为S△ABC+S△PAB+S△PAC+S△PBC=×2×2+××1+××1+×2×=2+2.
答案 2+2
三、解答题(本大题共6个小题,共70分)
17.(10分)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.
(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
证明 (1)取B1D1的中点O1,连接CO1,A1O1,
由于ABCD-A1B1C1D1是四棱柱,
所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,
所以A1O∥O1C,
又O1C?平面B1CD1,A1O 平面B1CD1,
所以A1O∥平面B1CD1.
(2)因为AC⊥BD,E,M分别为AD和OD的中点,
所以EM⊥BD,
又A1E⊥平面ABCD,BD?平面ABCD,
所以A1E⊥BD,
因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1,
又A1E,EM?平面A1EM,A1E∩EM=E,
所以B1D1⊥平面A1EM,
又B1D1?平面B1CD1,
所以平面A1EM⊥平面B1CD1.
18.(12分)一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
解 由题图知该多面体是底面为直角三角形的直三棱柱,其中AB=BC=BF=2,DE=CF=2,∠CBF=90°.
(1)证明 取BF的中点G,连接MG、NG.
由M、N分别为AF、BC的中点,
可得NG∥CF,MG∥AB,又AB∥EF,∴MG∥EF,∵MG∩NG=G,EF∩CF=F,∴平面MNG∥平面CDEF,MN?平面MNG,∴MN∥平面CDEF.
(2)取DE的中点H,连接AH.
因为AD=AE,所以AH⊥DE.
在直三棱柱ADE-BCF中,
平面ADE⊥平面CDEF,
平面ADE∩平面CDEF=DE,
所以AH⊥平面CDEF,
所以多面体A-CDEF是以AH为高,矩形CDEF为底面的棱锥.
AH=,S矩形CDEF=DE·EF=4,
所以棱锥A-CDEF的体积V=S矩形CDEF·AH=.
19.(12分)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
证明 连接OG并延长交AC于点M,连接QM,QO,OC,由G为△AOC的重心,得M为AC中点.
由Q为PA中点,得QM∥PC,
又O为AB中点,得OM∥BC.
因为QM∩MO=M,QM?平面QMO,MO?平面QMO,BC∩PC=C,BC?平面PBC,PC?平面PBC,
所以平面QMO∥平面PBC.
因为QG?平面QMO,所以QG∥平面PBC.
20.(12分)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
(1)证明 因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC?平面ABCD,所以AC⊥BE.又BE∩BD=B,所以AC⊥平面BED.又AC?平面AEC,所以平面AEC⊥平面BED.
(2)解 设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,由勾股定理可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC×GD×BE=x3=,故x=2.
从而可得AE=EC=ED=.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.
故三棱锥E-ACD的侧面积为3+2.
21.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=,求三棱锥P-ADM的体积.
解 (1)如图,过M作MN∥CD交PD于点N,连接AN.
∵PM=2MC,∴MN=CD.
又AB=CD,且AB∥CD,
∴AB綊MN,∴四边形ABMN为平行四边形,
∴BM∥AN.
又BM?平面PAD,AN?平面PAD,
∴BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
∵PD⊥平面ABCD,BE?平面ABCD,
∴PD⊥BE.
又AD?平面PAD,PD?平面
PAD,
AD∩PD=D.
∴BE⊥平面PAD.
由(1)知,BM∥平面PAD,
∴点M到平面PAD的距离等于点B到平面PAD的距离,即BE.
连接BD,在△ABD中,AB=AD=2,
∠BAD=,∴BE=,
则三棱锥P-ADM的体积VP-ADM=VM-PAD=×S△PAD×BE=×3×=.
22.(12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?并说明理由.
(1)证明 ∵D,E分别为AC,AB的中点,
∴DE∥BC.
又∵DE?平面A1CB,BC?平面A1CB,
∴DE∥平面A1CB.
(2)证明 由已知得AC⊥BC且DE∥BC,
∴DE⊥AC.
∴DE⊥A1D,DE⊥CD,A1D∩CD=D,
∴DE⊥平面A1DC.
而A1F?平面A1DC,
∴DE⊥A1F.
又∵A1F⊥CD,DE∩CD=D,
∴A1F⊥平面BCDE,BE?平面BCDE,
∴A1F⊥BE.
(3)解 线段A1B上存在点Q,使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又∵DE∥BC,
∴DE∥PQ.
∴平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,A1C?平面A1DC,
∴DE⊥A1C.
又∵P是等腰三角形DA1C底边A1C的中点,
∴A1C⊥DP,DE∩DP=D,
∴A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q(中点),使得A1C⊥平面DEQ.
章末检测(一)
一、选择题(本大题共12个小题,每小题5分,共60分)
1.设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;②若α∥β,β∥γ,m∥α,则m∥γ;③若m∥α,n∥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.① B.②和③
C.③和④ D.①和④
解析 ①正确;②若α∥β,β∥γ,m∥α,则m∥γ或m?γ,②错;③若m∥α,n∥α,则m∥n,而同平行于同一个平面的两条直线有三种位置关系,③错;④垂直于同一个平面的两个平面也可以相交,④错.
答案 A
2.在如右图所示的三棱锥A-BCD中,VA-BPQ=2,VC-APQ=6,VC-DPQ=12,则VA-BCD等于( )
A.20 B.24
C.28 D.56
解析 由==,得=,所以VP-BDQ=VP-CDQ=4,所以VA-BCD=2+6+12+4=24.
答案 B
3.如图,α∩β=l,A、B∈α,C∈β,且C?l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B
C.点C但不过点M D.点C和点M
解析 ∵AB?γ,M∈AB,∴M∈γ.
又α∩β=l,M∈l,∴M∈β.
根据公理3可知,点M在γ与β的交线上.
同理可知,点C也在γ与β的交线上.
答案 D
4.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
解析 如图,设截面圆的圆心为O′,
M为截面圆上任一点,
则OO′=,O′M=1,
∴OM==,
即球的半径为,∴V=π()3=4π.
答案 B
5.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.90° B.60°
C.45° D.30°
解析 连接B′C,则△AB′C为等边三角形,设AD=a,
则B′D=DC=a,B′C=AC=a,
所以∠B′DC=90°.
答案 A
6.如图,平面α⊥平面β,点A∈α,点B∈β,AB与两平面α,β所成的角分别为45°和30°.过点A,B分别作两平面交线的垂线,垂足为A′,B′,若AB=12,则A′B′=( )
A.4 B.6
C.8 D.9
解析 如图所示,连接A′B,AB′,
由题意得BB′⊥α,AA′⊥β,∠BAB′=45°,∠ABA′=30°,BB′⊥A′B′,AA′⊥A′B′,AA′⊥A′B.因为AB=12,所以BA′=AB·cos∠ABA′=6,BB′=ABsin∠BAB′=6,故A′B′==6.
答案 B
7.已知矩形ABCD,AB=1,BC=,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
解析 A错误,理由如下:过A作AE⊥BD,垂足为E,连接CE.
若直线AC与直线BD垂直,则可得BD⊥平面ACE,于是BD⊥CE,而由矩形ABCD边长的关系可知BD与CE并不垂直.所以直线AC与直线BD不垂直;B正确,理由如下:翻折到点A在平面BCD内的射影恰好在直线BC上时,平面ABC⊥平面BCD,此时由CD⊥BC可证CD⊥平面ABC,于是有AB⊥CD;C错误,理由如下:若直线AD与直线BC垂直,则由BC⊥CD可知BC⊥平面ACD,于是BC⊥AC,但是AB
答案 B
8.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2
C.2 D.2
解析 由三视图知可把四棱锥放在一个正方体内部,四棱锥为D-BCC1B1,最长棱为DB1=
==2.故选B.
答案 B
9.在长方体ABCD-A1B1C1D1中,AA1=2,AB=1,AD=4,则从A出发,沿长方体的表面到C1的最短距离是( )
A.5 B.7
C. D.
解析 两点之间,线段最短,在长方体展开图中,由A到C1的路线有三条,如下图,
三条路线长分别为
l1==,
l2==5,
l3==,
所以最短距离为5.
答案 A
10.已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B.3π
C. D.6π
解析 将三视图还原为直观图求体积.由三视图可知,此几何体(如图所示)是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的,所以V=×π×12×4=3π.
答案 B
11.如图所示,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有结论:
①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长,其中正确的是( )
A.①② B.①②③
C.① D.②③
解析 对于①,∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,
∵AB为圆O的直径,∴BC⊥AC,PA∩AC=A,
∴BC⊥平面PAC,
又PC?平面PAC,∴BC⊥PC,①正确;
对于②,∵点M为线段PB的中点,∴OM∥PA,
∵PA?平面PAC,OM?平面PAC,
∴OM∥平面PAC,②正确;
对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC的距离,故①②③都正确.
答案 B
12.已知二面角α-l-β为60°,动点P,Q分别在平面α,β内,P到β的距离为,Q到α的距离为2,则P,Q两点之间距离的最小值为( )
A. B.2
C.2 D.4
解析 如图,分别作QA⊥α于点A,AC⊥l于点C,PB⊥β于点B,PD⊥l于点D,连接CQ,BD,则∠ACQ=∠PDB=60°,AQ=2,BP=,∴AC=PD=2.又∵PQ==≥2.当且仅当AP=0,即点A与点P重合时取最小值.故选C.
答案 C
二、填空题(本大题共4个小题,每小题5分,共20分)
13.在△ABC中,∠BAC=90°,P为△ABC所在平面外一点,且PA=PB=PC,且平面PBC与平面ABC的位置关系是________.
解析 如右图所示,取BC的中点O,连接AO,PO.
∵PB=PC,∴PO⊥BC.
又△ABC是以A为直角顶点的直角三角形,
∴OA=OB,又PA=PB,
∴△POA≌△POB,
∴∠POA=∠POB=90°,
即PO⊥OA,而OA∩BC=O,
∴PO⊥平面ABC,而PO?平面PBC,
∴平面PBC⊥平面ABC.
答案 垂直
14.已知一个圆锥的展开图如图所示,其中扇形的圆心角为120°,底面圆的半径为1,则该圆锥的体积为________.
解析 因为扇形弧长为2π,设母线长为l,则有×2πl=2π,∴l=3,所以圆锥母线长为3,高为=2,所求体积V=×π×12×2=.
答案
15.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________(写出所有正确结论的编号).
解析 由条件可得AB⊥平面PAD,
∴AB⊥PD,故①正确;
若平面PBC⊥平面ABCD,由PB⊥BC,
得PB⊥平面ABCD,从而PA∥PB,这显然不成立,故②错;
S△PCD=CD·PD,S△PAB=AB·PA,
由AB=CD,PD>PA知③正确;
由E、F分别是棱PC、PD的中点,
可得EF∥CD,又AB∥CD,
∴EF∥AB,故AE与BF共面,故④错.
答案 ①③
16.某三棱锥的三视图如图所示,则该三棱锥的表面积是________.
解析 由三视图可得该三棱锥的直观图如图所示,其中PA=1,BC=2,取BC的中点M,连接AM,MP,则AM=2,AM⊥BC,故AC=AB===,由主视图和左视图可知PA⊥平面ABC,因此可得PC=PB===,PM===,所以三棱锥的表面积为S△ABC+S△PAB+S△PAC+S△PBC=×2×2+××1+××1+×2×=2+2.
答案 2+2
三、解答题(本大题共6个小题,共70分)
17.(10分)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.
(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
证明 (1)取B1D1的中点O1,连接CO1,A1O1,
由于ABCD-A1B1C1D1是四棱柱,
所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,
所以A1O∥O1C,
又O1C?平面B1CD1,A1O 平面B1CD1,
所以A1O∥平面B1CD1.
(2)因为AC⊥BD,E,M分别为AD和OD的中点,
所以EM⊥BD,
又A1E⊥平面ABCD,BD?平面ABCD,
所以A1E⊥BD,
因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1,
又A1E,EM?平面A1EM,A1E∩EM=E,
所以B1D1⊥平面A1EM,
又B1D1?平面B1CD1,
所以平面A1EM⊥平面B1CD1.
18.(12分)一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
解 由题图知该多面体是底面为直角三角形的直三棱柱,其中AB=BC=BF=2,DE=CF=2,∠CBF=90°.
(1)证明 取BF的中点G,连接MG、NG.
由M、N分别为AF、BC的中点,
可得NG∥CF,MG∥AB,又AB∥EF,∴MG∥EF,∵MG∩NG=G,EF∩CF=F,∴平面MNG∥平面CDEF,MN?平面MNG,∴MN∥平面CDEF.
(2)取DE的中点H,连接AH.
因为AD=AE,所以AH⊥DE.
在直三棱柱ADE-BCF中,
平面ADE⊥平面CDEF,
平面ADE∩平面CDEF=DE,
所以AH⊥平面CDEF,
所以多面体A-CDEF是以AH为高,矩形CDEF为底面的棱锥.
AH=,S矩形CDEF=DE·EF=4,
所以棱锥A-CDEF的体积V=S矩形CDEF·AH=.
19.(12分)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
证明 连接OG并延长交AC于点M,连接QM,QO,OC,由G为△AOC的重心,得M为AC中点.
由Q为PA中点,得QM∥PC,
又O为AB中点,得OM∥BC.
因为QM∩MO=M,QM?平面QMO,MO?平面QMO,BC∩PC=C,BC?平面PBC,PC?平面PBC,
所以平面QMO∥平面PBC.
因为QG?平面QMO,所以QG∥平面PBC.
20.(12分)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
(1)证明 因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC?平面ABCD,所以AC⊥BE.又BE∩BD=B,所以AC⊥平面BED.又AC?平面AEC,所以平面AEC⊥平面BED.
(2)解 设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,由勾股定理可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC×GD×BE=x3=,故x=2.
从而可得AE=EC=ED=.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.
故三棱锥E-ACD的侧面积为3+2.
21.(12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=,求三棱锥P-ADM的体积.
解 (1)如图,过M作MN∥CD交PD于点N,连接AN.
∵PM=2MC,∴MN=CD.
又AB=CD,且AB∥CD,
∴AB綊MN,∴四边形ABMN为平行四边形,
∴BM∥AN.
又BM?平面PAD,AN?平面PAD,
∴BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
∵PD⊥平面ABCD,BE?平面ABCD,
∴PD⊥BE.
又AD?平面PAD,PD?平面
PAD,
AD∩PD=D.
∴BE⊥平面PAD.
由(1)知,BM∥平面PAD,
∴点M到平面PAD的距离等于点B到平面PAD的距离,即BE.
连接BD,在△ABD中,AB=AD=2,
∠BAD=,∴BE=,
则三棱锥P-ADM的体积VP-ADM=VM-PAD=×S△PAD×BE=×3×=.
22.(12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?并说明理由.
(1)证明 ∵D,E分别为AC,AB的中点,
∴DE∥BC.
又∵DE?平面A1CB,BC?平面A1CB,
∴DE∥平面A1CB.
(2)证明 由已知得AC⊥BC且DE∥BC,
∴DE⊥AC.
∴DE⊥A1D,DE⊥CD,A1D∩CD=D,
∴DE⊥平面A1DC.
而A1F?平面A1DC,
∴DE⊥A1F.
又∵A1F⊥CD,DE∩CD=D,
∴A1F⊥平面BCDE,BE?平面BCDE,
∴A1F⊥BE.
(3)解 线段A1B上存在点Q,使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又∵DE∥BC,
∴DE∥PQ.
∴平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,A1C?平面A1DC,
∴DE⊥A1C.
又∵P是等腰三角形DA1C底边A1C的中点,
∴A1C⊥DP,DE∩DP=D,
∴A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q(中点),使得A1C⊥平面DEQ.
