湘教版九年级上册数学《第4章锐角三角函数》单元测试题含答案
文档属性
| 名称 | 湘教版九年级上册数学《第4章锐角三角函数》单元测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 190.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-25 22:25:26 | ||
图片预览



文档简介
第4章 锐角三角函数
一、选择题
1.tan60°的值等于( )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.在Rt△ABC中,∠C=90o , AC=4,AB=5,则sinB的值是 ?( ? ?? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
3.如果∠α是等腰直角三角形的一个锐角,则cosα的值是()
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?
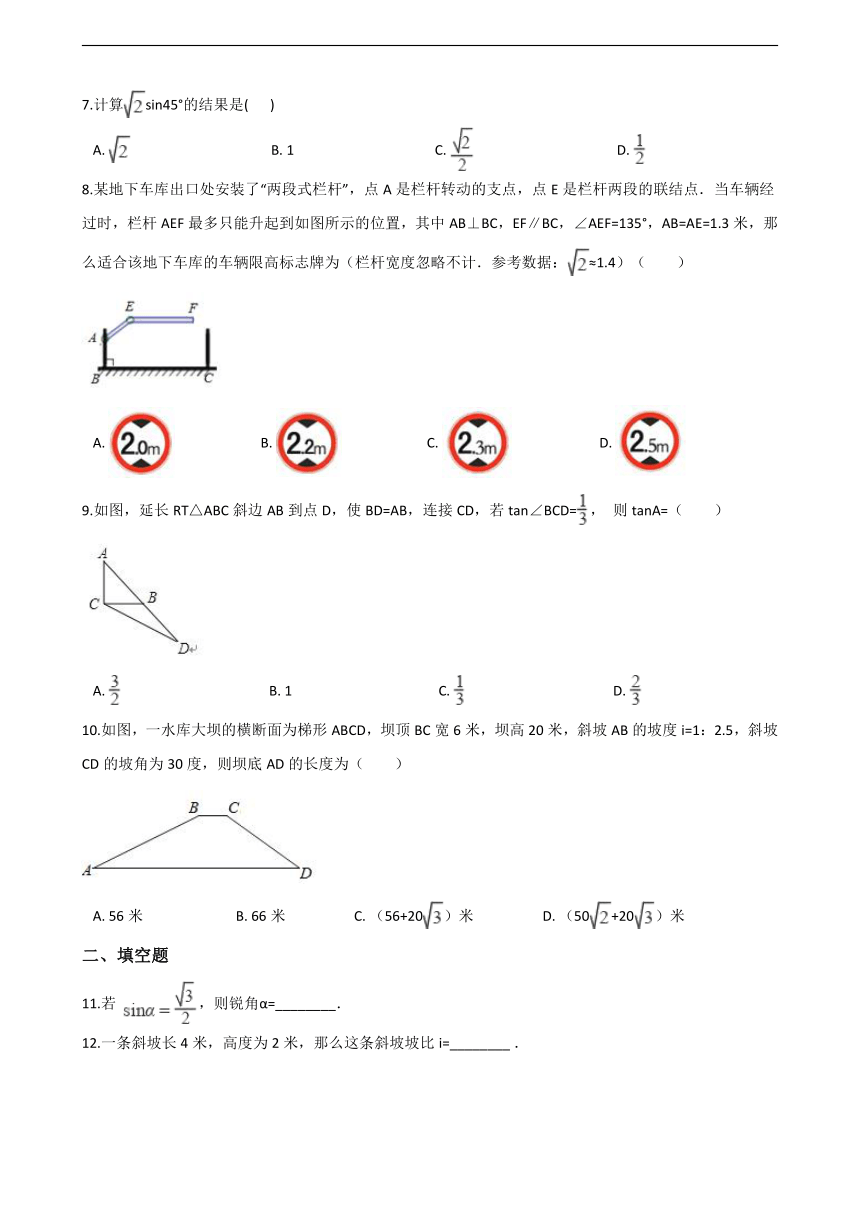
4.如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
A.?1.2???????????????????????????????????????B.?1.1???????????????????????????????????????C.?0.8???????????????????????????????????????D.?2.2
5.在△ABC中,∠C=90°,AB=15,sinA= , 则BC等于( )
A.?45 ???????????????????????????B.?5 ???????????????????????????C.? ???????????????????????????D.?
6.王芳同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王芳同学离A地(??) ?
A.?50?m???????????????????????????????B.?100m???????????????????????????????C.?150m???????????????????????????????D.?100?m
7.计算sin45°的结果是(???? )
A.??????????????????????????????????????????B.?1?????????????????????????????????????????C.??????????????????????????????????????????D.?
8.某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:≈1.4)( )
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
9.如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=, 则tanA=( )
A.???????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
10.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
A.?56米???????????????????????????B.?66米????????????????????C.?(56+20)米????????????????????D.?(50+20)米
二、填空题
11.若 ,则锐角α=________.
12.一条斜坡长4米,高度为2米,那么这条斜坡坡比i=________?.
13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=, 那么BC=________?
14.如图,河堤横断面如图所示,迎水坡AB的坡比为1:,则坡角∠A的度数为________
15.在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
16.如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是________米(结果保留根号).
17.在Rt 中, , ,则 的值为________.
18.在正方形网格中,△ABC的位置如图所示,则tanB的值为________.
19.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为________厘米(结果保留根号).
三、解答题
20.如图,已知∠B=90°,AB=2cm,BC=2cm,CD=3cm,AD=5cm,求四边形ABCD的面积.
21.马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
22.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=, AD=4. (1)求BC的长; (2)求tan∠DAE的值.
23.随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.
(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
24.如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度
1:20
1:16
1:12
最大高度(米)
1.50
1.00
0.75
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
参考答案
一、选择题
D D B B B D B B A C
二、填空题
11. 60° 12. 1: 13. 6 14. 30 15. 24
16. 200( +1) 17. 18. 19. 38
三、解答题
20. 解:连接AC, 在△ABC中, ∵∠B=90°,AB=2cm,BC=2cm, ∴AC=4cm, 在△ACD中,AC2+CD2=42+32=25,AD2=25, ∴AC2+CD2=AD2 , ∴∠ACD=90°, ∴S四边形ABCD=S△ABC+S△ACD=×AB×BC+×AC×CD =×2×2+×4×3=2+6(cm2).
21. 解:过点P作PC⊥AB , 垂足为C , 设PC=x海里. 在Rt△APC中,∵tan∠A= , ∴AC= . 在Rt△PCB中,∵tan∠B= , ∴BC= . ∵AC+BC=AB=21×5, ∴ , 解得 . ∵ , ∴ (海里). ∴向阳号轮船所处位置B与城市P的距离为100海里.
22. (1)在△ABC中,∵AD是BC边上的高, ∴∠ADB=∠ADC=90°. 在△ADC中,∵∠ADC=90°,∠C=45°,AD=4, ∴DC=AD=4. 在△ADB中,∵∠ADB=90°,sinB=, AD=4, ∴AB=? ∴BD=, ∴BC=BD+DC= (2)∵AE是BC边上的中线, ∴CE=BC=, ∴DE=CE-CD=, ∴tan∠DAE=.
23. (1)解 :过A作AD⊥CB,垂足为点D. ???????? ∵在Rt△ABD中,∠BAD=30°, ∴AB=2BD ∵在Rt△ABC中,∠CBA=60°, ∴∠ACB=30° ∴BC=2AB ,又∵BC=30米 , ∴AB=15米 ∴BD=7.5米 ∴CD=BC-BD=30-7.5=22.5米 答:无人机的竖直高度CD为22.5米。 (2)解 :设CD=x,则 BD=m-x , 在Rt△ABD中,∠BAD=α, ∴tanα==; 在Rt△ADC中,∠DCA=β , ∴tanβ==, ∴, tanβ·(m-x)=tanα·x ∴x=
24. (1)解:∵第一层有十级台阶,每级台阶的高为0.15米, ∴最大高度为0.15×10=1.5(米), 由表知建设轮椅专用坡道AB选择符合要求的坡度是1:20; (2)解:如图, 过B作BE⊥AD于E,过C作CF⊥AD于F, ∴BE=CF=1.5,EF=BC=2, ∵ = , ∴ = , ∴AE=DF=30, ∴AD=AE+EF+DF=60+2=62, 答:斜坡底部点A与台阶底部点D的水平距离AD为62米.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
