湘教版九年级上册数学《第3章图形的相似》单元测试题含答案
文档属性
| 名称 | 湘教版九年级上册数学《第3章图形的相似》单元测试题含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 161.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-25 00:00:00 | ||
图片预览



文档简介
第3章 图形的相似
一、选择题
1.在1:1000000的地图上,A,B两点之间的距离是5cm,则A,B两地的实际距离是( )
A.?5km????????????????????????????????B.?50km????????????????????????????????C.?500km????????????????????????????????D.?5000km
2.下列说法错误的是( )
A.?两个等边三角形一定相似????????????????????????????????????B.?两个等腰三角形一定相似 C.?两个等腰直角三角形一定相似?????????????????????????????D.?两个全等三角形一定相似
3.若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.?1:2????????????????????????????????????B.?1:4????????????????????????????????????C.?2:1????????????????????????????????????D.?4:1
4.已知△ABC∽△DEF,如果∠A=55o,∠B=100o,则∠F=(????)
A.?55o??????????????????????????????????????B.?100o??????????????????????????????????????C.?25o??????????????????????????????????????D.?30o
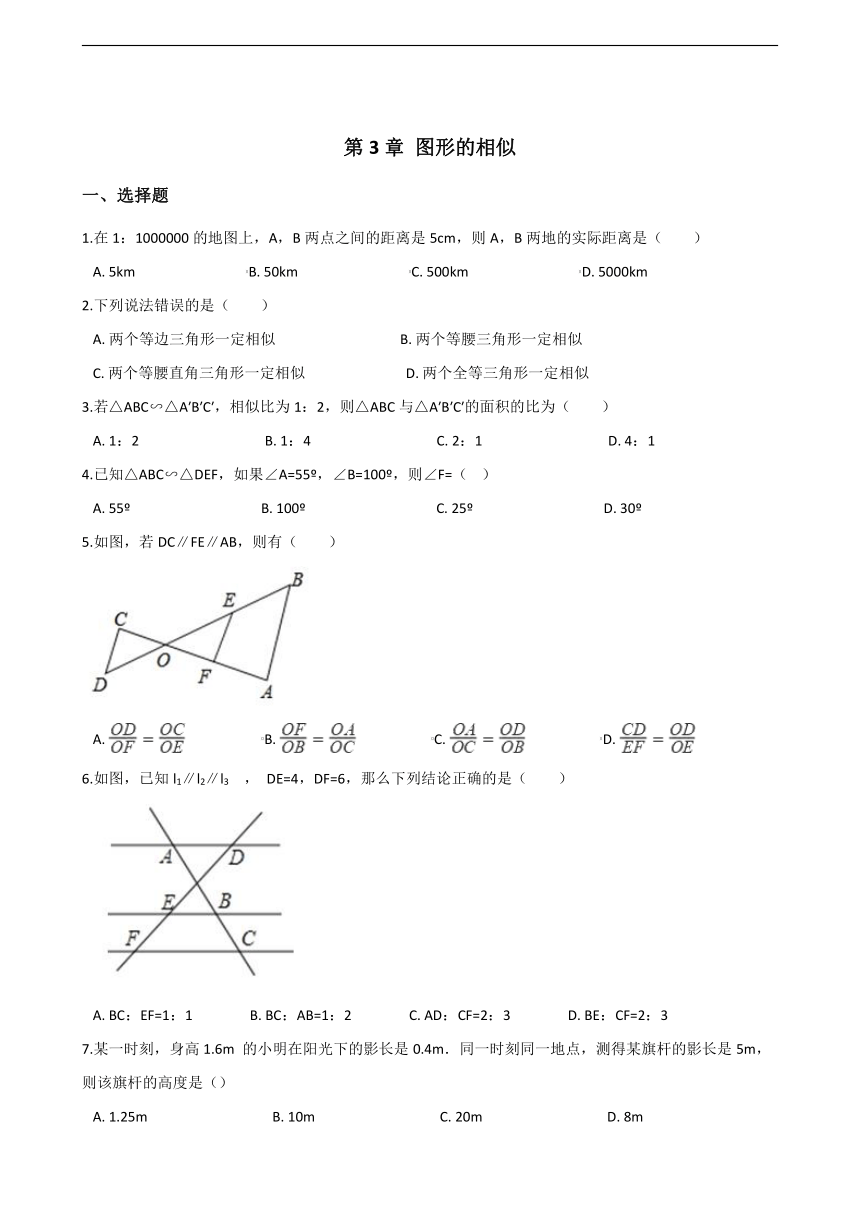
5.如图,若DC∥FE∥AB,则有( )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
6.如图,已知l1∥l2∥l3 , DE=4,DF=6,那么下列结论正确的是( ) ?
A.?BC:EF=1:1????????????????B.?BC:AB=1:2????????????????C.?AD:CF=2:3????????????????D.?BE:CF=2:3
7.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()
A.?1.25m????????????????????????????????????B.?10m????????????????????????????????????C.?20m????????????????????????????????????D.?8m
8.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S四边形DBCE=8S△ADE . 那么AE:AC的值为( )
A.?1:8????????????????????????????????????B.?1:4????????????????????????????????????C.?1:3????????????????????????????????????D.?1:9
9.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A , BC=3,AC=6,则CD的长为( )
A.?1??????????????????????????????????????B.?2??????????????????????????????????????C.???????????????????????????????????????D.?
10.如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( ) ?
A.?1:2??????????????????????????????????B.?1:3??????????????????????????C.?2:3??????????????????????????????????D.?以上都不正确
二、填空题
11.若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=2cm,则d=________?.
12.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是________.
13.已知实数a,b,c满足a+b+c=10,且 ,则 的值是________?
14.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________?. ?
15.如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 =________?.
16.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度). ①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________?; ②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1________?,点C2的坐标是________??; ③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________?.
17.如图,已知D , E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB , 那么BC:CD应等于________.
18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________?. ?
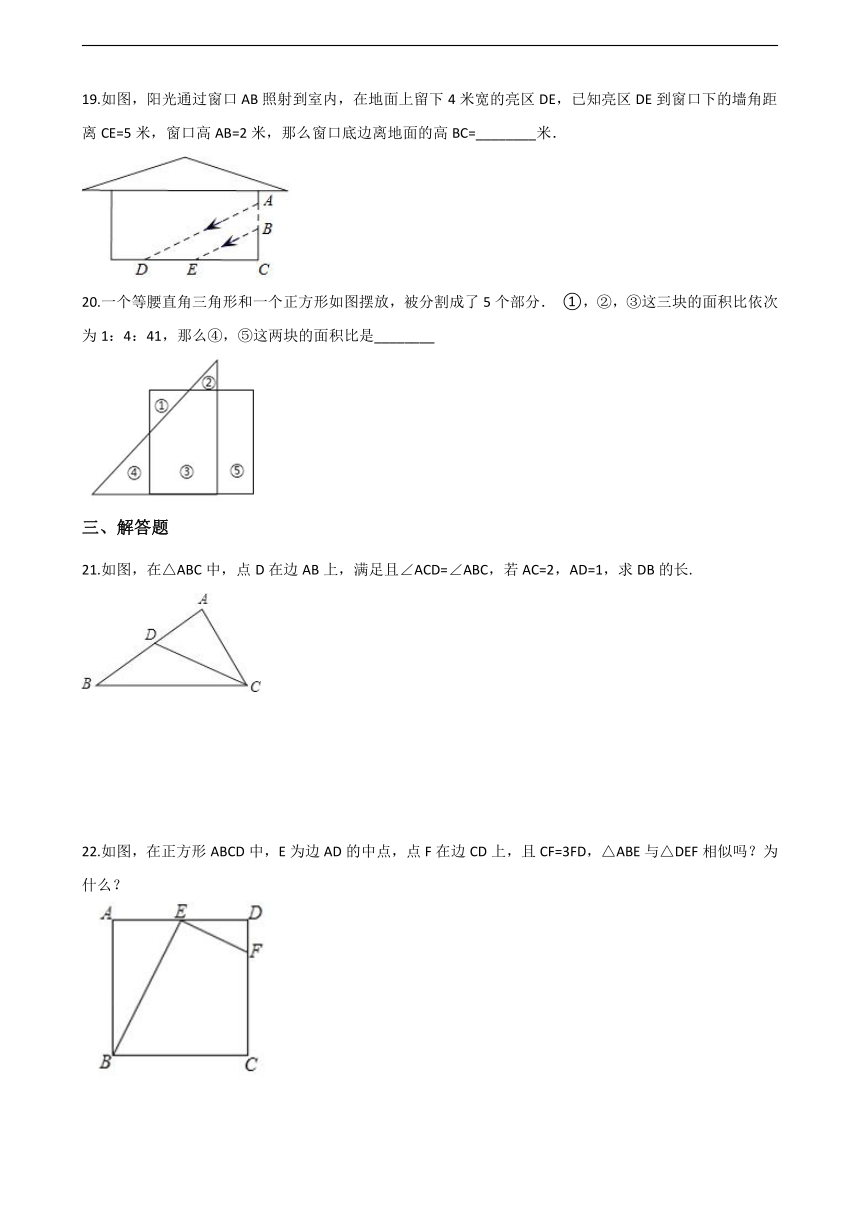
19.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=________米.
20.一个等腰直角三角形和一个正方形如图摆放,被分割成了5个部分. ①,②,③这三块的面积比依次为1:4:41,那么④,⑤这两块的面积比是________?
三、解答题
21.如图,在△ABC中,点D在边AB上,满足且∠ACD=∠ABC,若AC=2,AD=1,求DB的长.
22.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?
23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
24.已知:如图,. (1)求证:; (2)当时,求证:ECBC.
25.在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.
(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
参考答案
一、选择题
B B B C D B C C C C
二、填空题
11. 4cm
12. 1:9
13.
14.
15. .
16.(2,﹣2);
;
(1,0);?(2a﹣3,2b﹣4)
17.
18.
19. 2.5
20. 9:14
三、解答题
21.解∵∠ACD=∠ABC,∠BAC=∠CAD,∴△ADC∽△ACB.∴. ∵AC=2,AD=1,∴. ∴DB=AB-AD=3.
22. 解:△ABE与△DEF相似.理由如下: ∵四边形ABCD为正方形, ∴∠A=∠D=90°,AB=AD=CD, 设AB=AD=CD=4a, ∵E为边AD的中点,CF=3FD, ∴AE=DE=2a,DF=a, ∴=2,=2, ∴ 而∠A=∠D, ∴△ABE∽△DEF.
23. 解:∵△PCD是等边三角形, ∴∠PCD=60°, ∴∠ACP=120°, ∵△ACP∽△PDB, ∴∠APC=∠B,又∠A=∠A, ∴△ACP∽△ABP, ∴∠APB=∠ACP=120°
24. 证明:(1)∵ ∴△ABC∽△DEF??? ∴, (2)∵BAC=DAE?? ∴BAD=CAE? 又∵ ∴? ∴△ABD∽△ACE? ∴ABD=ACE ∵BAC=90° ∴ABD+ACD=90°????? ∴ACE+ACD=90°? 即ECBC.
25. (1)证明:感知:如图①,∵四边形ABCD为矩形, ∴∠D=∠C=90°, ∴∠DAE+∠DEA=90°, ∵EF⊥AE, ∴∠AEF=90°, ∴∠DEA+∠FEC=90°, ∴∠DAE=∠FEC, ∵DE=1,CD=4, ∴CE=3, ∵AD=3, ∴AD=CE, ∴△ADE≌△ECF(ASA) (2)探究:如图②,∵四边形ABCD为矩形, ∴∠D=∠C=90°, ∴∠DPE+∠DEP=90°, ∵EF⊥PE, ∴∠PEF=90°, ∴∠DEP+∠FEC=90°, ∴∠DPE=∠FEC, ∴△PDE∽△ECF (3)2
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
