2018-2019学年新高一开学第一周 数学 人教版必修1 1.1.3集合的基本运算 第一课时 交集与并集 课件
文档属性
| 名称 | 2018-2019学年新高一开学第一周 数学 人教版必修1 1.1.3集合的基本运算 第一课时 交集与并集 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-27 20:34:56 | ||
图片预览








文档简介
课件20张PPT。1.1 集合
1.1.3 集合的基本运算
第一课时 交集与并集第一章 集合与函数概念人教版 必修一教学目标1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
2.能使用Venn图表示集合的并集和交集,体会直观图对理解抽象概念的作用.
3.掌握有关的术语和符号,并会用它们正确进行集合的并集与交集运算.课件简介 本节课主要是通过观察和类比,借助Venn图理解集合的交集及并集运算,培养数形结合的思想;体会类比的作用;感受集合作为一种语言在表示数学内容时的简洁性和准确性.
利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等条件,解答时常借助于交集、并集的定义及集合间的关系去分析,将关系进行等价转化如:A∩B=A?A?B,A∪B=B?A?B等.
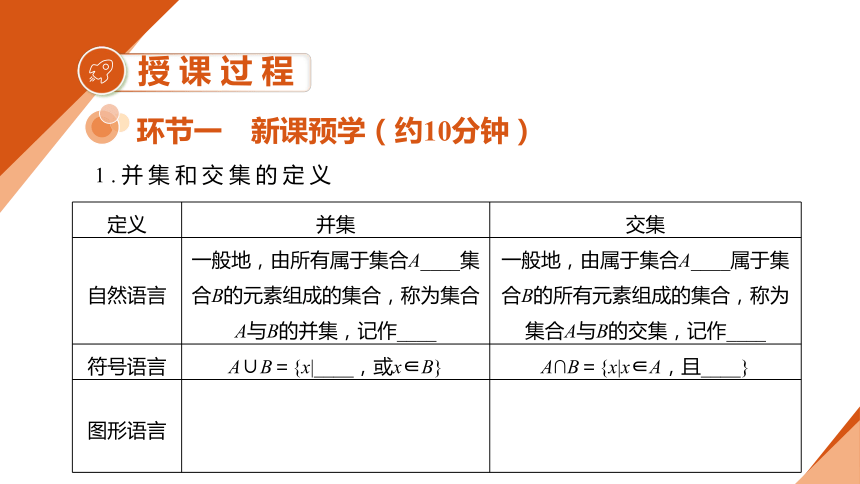
(2)关注点:当题目条件中出现B?A时,如果集合A是一个确定的集合,而集合B不确定,解答时要注意讨论B=?的情况.授课过程1.并集和交集的定义2.并集和交集的性质AAA?例1 (1)设集合A={1,2,3},B={2,3,4,5},求A∪B;
(2)设集合A={x|-3(2)画出数轴如图所示:∴A∪B={x|-3并集运算应注意的问题
(1)求两个集合的并集时要注意利用集合元素的互异性这一属性,重复的元素只能算一个.
(2)对于元素个数无限的集合进行并集运算时,可借助数轴,利用数轴分析法求解,但要注意端点的值能否取到.理解升华变式训练1 (1)已知集合A={0,2,4},B={0,1,2,3,5},则A∪B=________.
(2)若集合A={x|-1≤x<2},B={x|0<x≤3},则A∪B=________.
(3)已知集合A={1,3,0},B={1,m},A∪B=A,则m=( )
A.0或 1 B.0或3
C.3 D.0解析:(1){0,1,2,3,4,5} (2){x|-1≤x≤3} (3)B例2 (1)设集合M={-1,0,1},N={x|x2=x}则M∩N=( )
A.{-1,0,1} B.{0,1}
C.{1} D.{0}
(2)若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于( )
A.{x|x≤3或x>4} B.{x|-1 C.{x|3≤x<4} D.{x|-2≤x<-1}
(3)已知A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则A∩B=________.重点探究二 交集解析: (1)N={x|x2=x}={0,1},
∴M∩N={0,1}故选B.
(2)将集合A、B表示在数轴上,
由数轴可得A∩B={x|-2≤x<-1},故选D.
求集合A∩B的方法与步骤
(1)步骤
①首先要搞清集合A、B的代表元素是什么;
②把所求交集的集合用集合符号表示出来,写成“A∩B”的形式;
③把化简后的集合A、B的所有公共元素都写出来即可(若无公共元素则所求交集为?).
(2)方法
①若A、B的代表元素是方程的根,则应先解方程求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
②若A、B是无限数集,可以利用数轴来求解但要注意,利用数轴表示不等式时,含有端点的值用实点表示,不含有端点的值用虚点表示.理解升华变式训练2 (1)若综合M={x|(x+4)(x+1)=0},N={x|(x-4)(x-1)=0},则M∩N=( )
A.{1,4} B.{-1,-4}
C.{0} D.?
(2)已知集合A={x|1<x<3},B={x|2<x<5},则A∩B=( )
A.{2} B.{x|1<x<3}
C.{x|2<x<3} D.{x|3<x<5}
(3)已知A={x|x是等腰三角形},B={x|x是直角三角形},则A∩B=________.解析: (1)M={-4,-1},N={4,1},M∩N=?,故选D.
(2)在数轴上表示集合A、B,如下图所示,则A∩B={x|2<x<3},故选C.
(3)既是等腰又是直角的三角形为等腰直角三角形.所以A∩B={x|x是等腰直角三角形}.
答案:(1)D (2)C (3){x|x是等腰直角三角形}重点探究三 并集和交集的性质与应用例3 已知集合A={x|x2-3x+2=0},B={x|ax-2=0},且A∪B=A,求实数a组成的集合C.解析:由x2-3x+2=0,得x=1或x=2,
∴A={1,2}.
又A∪B=A,∴B?A.
(1)若B=?,即方程ax-2=0无解,此时a=0.
(2)若B≠?,则B={1}或B={2}.
当B={1}时,有a-2=0,即a=2;
当B={2}时,有2a-2=0,即a=1.
综上可知,适合题意的实数a所组成的集合C={0,1,2}.
(1)在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等,解答时应灵活处理.
(2)当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.理解升华变式训练3 设集合A={-2},B={x|ax+1=0},
(1)若A∪B=B,求a的值;
(2)若A∩B=B,求a的值.解析:(1)∵A∪B=B,
∴A?B.
∴-2是方程ax+1=0的根,
∴a=12.1.已知集合A={1,2,4},B={2,4,6},则A∪B=________.{1,2,4,6}2.设集合A={y|y=x2,x∈R},B={(x, y)|y=x+2,x∈R}, 则A∩B=________.?3.设A={x|x>0},B={x|x≤1},求A∩B 和A∪B.解析:A∩B ={x|x>0}∩{x|x≤1}={x|0A∪B={x|x>0}∪{x|x≤1}=R.4.设集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0,a ∈R},若A∩B =B,求a的值.课堂笔记
1.1.3 集合的基本运算
第一课时 交集与并集第一章 集合与函数概念人教版 必修一教学目标1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
2.能使用Venn图表示集合的并集和交集,体会直观图对理解抽象概念的作用.
3.掌握有关的术语和符号,并会用它们正确进行集合的并集与交集运算.课件简介 本节课主要是通过观察和类比,借助Venn图理解集合的交集及并集运算,培养数形结合的思想;体会类比的作用;感受集合作为一种语言在表示数学内容时的简洁性和准确性.
利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等条件,解答时常借助于交集、并集的定义及集合间的关系去分析,将关系进行等价转化如:A∩B=A?A?B,A∪B=B?A?B等.
(2)关注点:当题目条件中出现B?A时,如果集合A是一个确定的集合,而集合B不确定,解答时要注意讨论B=?的情况.授课过程1.并集和交集的定义2.并集和交集的性质AAA?例1 (1)设集合A={1,2,3},B={2,3,4,5},求A∪B;
(2)设集合A={x|-3
(1)求两个集合的并集时要注意利用集合元素的互异性这一属性,重复的元素只能算一个.
(2)对于元素个数无限的集合进行并集运算时,可借助数轴,利用数轴分析法求解,但要注意端点的值能否取到.理解升华变式训练1 (1)已知集合A={0,2,4},B={0,1,2,3,5},则A∪B=________.
(2)若集合A={x|-1≤x<2},B={x|0<x≤3},则A∪B=________.
(3)已知集合A={1,3,0},B={1,m},A∪B=A,则m=( )
A.0或 1 B.0或3
C.3 D.0解析:(1){0,1,2,3,4,5} (2){x|-1≤x≤3} (3)B例2 (1)设集合M={-1,0,1},N={x|x2=x}则M∩N=( )
A.{-1,0,1} B.{0,1}
C.{1} D.{0}
(2)若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于( )
A.{x|x≤3或x>4} B.{x|-1
(3)已知A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则A∩B=________.重点探究二 交集解析: (1)N={x|x2=x}={0,1},
∴M∩N={0,1}故选B.
(2)将集合A、B表示在数轴上,
由数轴可得A∩B={x|-2≤x<-1},故选D.
求集合A∩B的方法与步骤
(1)步骤
①首先要搞清集合A、B的代表元素是什么;
②把所求交集的集合用集合符号表示出来,写成“A∩B”的形式;
③把化简后的集合A、B的所有公共元素都写出来即可(若无公共元素则所求交集为?).
(2)方法
①若A、B的代表元素是方程的根,则应先解方程求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
②若A、B是无限数集,可以利用数轴来求解但要注意,利用数轴表示不等式时,含有端点的值用实点表示,不含有端点的值用虚点表示.理解升华变式训练2 (1)若综合M={x|(x+4)(x+1)=0},N={x|(x-4)(x-1)=0},则M∩N=( )
A.{1,4} B.{-1,-4}
C.{0} D.?
(2)已知集合A={x|1<x<3},B={x|2<x<5},则A∩B=( )
A.{2} B.{x|1<x<3}
C.{x|2<x<3} D.{x|3<x<5}
(3)已知A={x|x是等腰三角形},B={x|x是直角三角形},则A∩B=________.解析: (1)M={-4,-1},N={4,1},M∩N=?,故选D.
(2)在数轴上表示集合A、B,如下图所示,则A∩B={x|2<x<3},故选C.
(3)既是等腰又是直角的三角形为等腰直角三角形.所以A∩B={x|x是等腰直角三角形}.
答案:(1)D (2)C (3){x|x是等腰直角三角形}重点探究三 并集和交集的性质与应用例3 已知集合A={x|x2-3x+2=0},B={x|ax-2=0},且A∪B=A,求实数a组成的集合C.解析:由x2-3x+2=0,得x=1或x=2,
∴A={1,2}.
又A∪B=A,∴B?A.
(1)若B=?,即方程ax-2=0无解,此时a=0.
(2)若B≠?,则B={1}或B={2}.
当B={1}时,有a-2=0,即a=2;
当B={2}时,有2a-2=0,即a=1.
综上可知,适合题意的实数a所组成的集合C={0,1,2}.
(1)在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A∩B=A?A?B,A∪B=B?A?B等,解答时应灵活处理.
(2)当集合B?A时,如果集合A是一个确定的集合,而集合B不确定,运算时要考虑B=?的情况,切不可漏掉.理解升华变式训练3 设集合A={-2},B={x|ax+1=0},
(1)若A∪B=B,求a的值;
(2)若A∩B=B,求a的值.解析:(1)∵A∪B=B,
∴A?B.
∴-2是方程ax+1=0的根,
∴a=12.1.已知集合A={1,2,4},B={2,4,6},则A∪B=________.{1,2,4,6}2.设集合A={y|y=x2,x∈R},B={(x, y)|y=x+2,x∈R}, 则A∩B=________.?3.设A={x|x>0},B={x|x≤1},求A∩B 和A∪B.解析:A∩B ={x|x>0}∩{x|x≤1}={x|0
