2018-2019学年物理 第二节时间和位移 教案 Word版
文档属性
| 名称 | 2018-2019学年物理 第二节时间和位移 教案 Word版 |  | |
| 格式 | zip | ||
| 文件大小 | 204.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-08-26 19:56:32 | ||
图片预览

文档简介
【学习目标】
1.知道时间和时刻的区别和联系。
2.理解位移的概念,了解路程与位移的区别。
3.知道标量和矢量。
4.能用数轴或一维直线坐标表示时刻和时间、位置和位移。
5.知道时刻与位置、时间与位移的对应关系。
【重点、难点分析】
学习重点:
1.时间和时刻的概念以及它们之间的区别和联系。
2.位移的概念以及它与路程的区别。
学习难点:
正确认识生活中的时间与时刻.理解位移的概念,会用有向线段表示位移。
先通读课本,按要求预习导学案中自主学习部分,按指导要求完成合作探究。
一、阅读P12第一部分:时刻和时间间完隔并成下列问题。
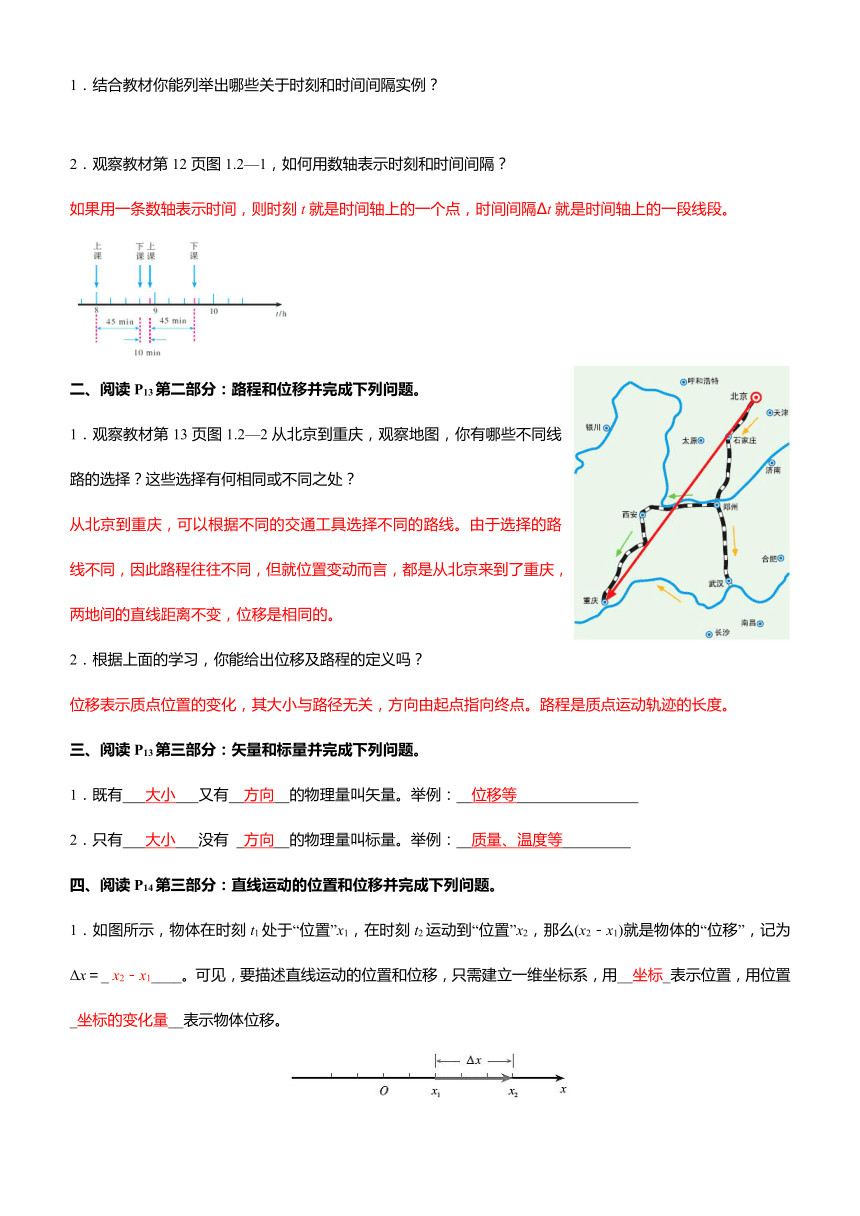
1.结合教材你能列举出哪些关于时刻和时间间隔实例?
2.观察教材第12页图1.2—1,如何用数轴表示时刻和时间间隔?
如果用一条数轴表示时间,则时刻t就是时间轴上的一个点,时间间隔Δt就是时间轴上的一段线段。
二、阅读P13第二部分:路程和位移并完成下列问题。
1.观察教材第13页图1.2—2从北京到重庆,观察地图,你有哪些不同线路的选择?这些选择有何相同或不同之处?
从北京到重庆,可以根据不同的交通工具选择不同的路线。由于选择的路线不同,因此路程往往不同,但就位置变动而言,都是从北京来到了重庆,两地间的直线距离不变,位移是相同的。
2.根据上面的学习,你能给出位移及路程的定义吗?
位移表示质点位置的变化,其大小与路径无关,方向由起点指向终点。路程是质点运动轨迹的长度。
三、阅读P13第三部分:矢量和标量并完成下列问题。
1.既有 大小 又有 方向 的物理量叫矢量。举例: 位移等
2.只有 大小 没有 方向 的物理量叫标量。举例: 质量、温度等
四、阅读P14第三部分:直线运动的位置和位移并完成下列问题。
1.如图所示,物体在时刻t1处于“位置”x1,在时刻t2运动到“位置”x2,那么(x2-x1)就是物体的“位移”,记为Δx=_ x2-x1____。可见,要描述直线运动的位置和位移,只需建立一维坐标系,用__坐标_表示位置,用位置_坐标的变化量__表示物体位移。
1. 时刻和时间间隔(观看微课《时间与时刻》)
时间和时刻有区别,也有联系,在时间轴上,时间表示一段,时刻表示一个点。如图所示,0点表示开始计时,0~3表示3 s的时间,即前3 s。2~3表示第3 s,不管是前3 s,还是第3 s,这都是指 时间 。3 s所对应的点计为3 s末,也为4 s初,这就是 时刻 。
2. 路程和位移
(1)在坐标系中,我们也可以用数学的方法表示出位移。
实例:观察教材第13页图1.2—3质点从A点运动到B点,我们可以用从_初位置__A指向__末位置_B的__有向_线段表示位移。
(2)阅读下面的对话:
甲:请问到市图书馆怎么走?
乙:从你所在的市中心向南走400 m到一个十字路口,再向东走300 m就到了。
甲:谢谢!
乙:不用客气。
请在图上把甲要经过的路程和位移表示出来。并归纳一下:位移和路程有什么不同?
路 程
位 移
意义
表示路径的长度
表示位置的变化
大小
等于运动轨迹的长度
等于从初位置到末位置的有向线段的长度
方向
无方向
从初位置指向末位置
3. 矢量和标量
(1)一塑料桶中原来有4 kg水,又加入3 kg水。问这只塑料桶中共有多少水?
质量是标量,两个标量相加遵从算术运算的法则,故又加入3 kg水后塑料桶中共有7 kg水。
(2)一位同学从操场中心A出发,向北走了40 m,到达C点,然后又向东走了30 m,到达B点。用有向线段表明他第一次、第二次的位移和两次行走的合位移(即代表他的位置变化的最后结果的位移)。这位同学由A到B的位移和路程的大小各是多少?
这位同学经过的路程为40 m + 30 m = 70 m
位移为。
(3)某人在晨练,按如图所示路径行走在半径为R的中国古代八卦图上,中央的S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向。他从A点出发沿曲线ABCOADC行进,则当他走到D点时,他的路程和位移的大小分别为多少?位移的方向如何?
路程就是由A到D的轨迹长度,位移的大小为由A到D的线段长度,位移方向由A指向D。路程是标量,等于半径为R的圆周长与半径为的两半圆周长之和减去半径为R的圆周长的,即。位移是矢量,大小为AD线段长度,由直角三角形知识得AD =R,方向由A指向D,即东南方向。故路程和位移的大小分别为和R,位移的方向为东南方向,即东偏南45°。
你能通过这几个实例比较出算术相加与矢量相加的法则吗?
标量运算遵守算术运算法则,矢量运算遵守三角形定则。
4. 直线运动中的位置和位移
如图所示,一辆汽车在马路上行驶。t = 0时,汽车在十字路口中心的左侧20 m处。2 s后,汽车正好到达十字路口的中心;再过3 s后,汽车行驶到了十字路口中心右侧30 m处。如果把这条马路抽象为一条坐标轴x,十字路口中心定为坐标轴的原点,向右为x轴的正方向,试将汽车在三个观测时刻的位置坐标填入下表,并计算汽车5 s内的位移。
观测时刻
t = 0时
过2 s
再过3 s
坐标位置
x1 = -20 m
x2 = 0
x3 = 30 m
解析:x1=- 20 m,x2=0,x3=30 m,汽车5 s内的位移Δx= x3- x1 = 50 m。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
