苏科版八年级数学上册《第6章一次函数》测试题含答案
文档属性
| 名称 | 苏科版八年级数学上册《第6章一次函数》测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-27 05:32:13 | ||
图片预览

文档简介
苏科版八年级数学上册第6章一次函数测试题
一、选择题(每小题4分,共28分)
1.下列函数表达式:①y=-x;②y=3x+11;③y=x2+x+1;④y=. 其中属于一次函数的有( )
A.1个 B.2个 C.3个 D.4个
2.若点(m,n)在函数y=2x+1的图像上,则2m-n的值是( )
A.2 B.-2 C.1 D.-1
3.如图,直线l经过第一、二、四象限,l的函数表达式是y=(m-3)x+m+2,则m的取值范围在数轴上表示为( )
4.若实数a,b满足ab<0,则一次函数y=ax+b的图像可能是( )
5.如图,函数y=2x和y=ax+4的图像相交于点A(m,3),则不等式2xA.x< B.x<3 C.x> D.x>3
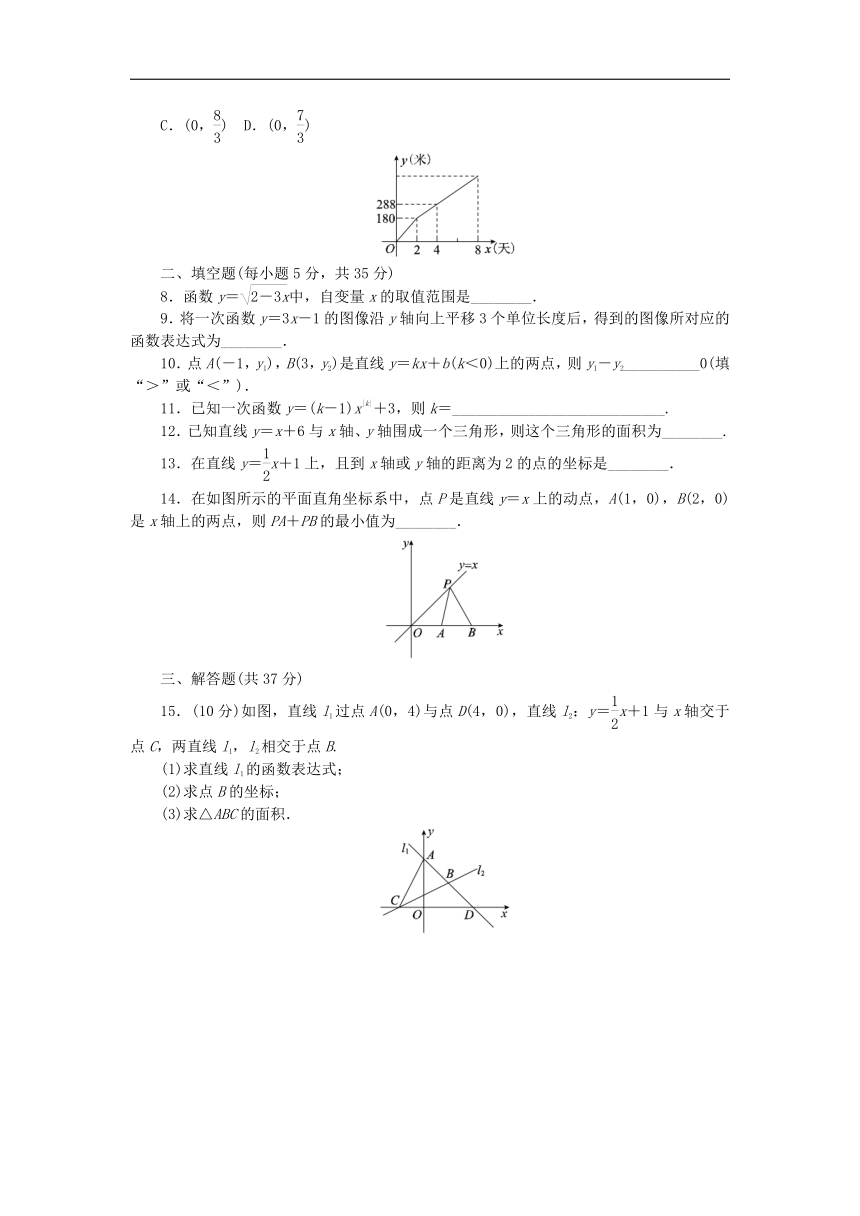
6.如图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的函数关系图像.根据图像提供的信息,可知该公路的长度是( )
A.365米 B.500米 C.504米 D.684米
7.如图,在平面直角坐标系中,已知一次函数y=-x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A.(0,3) B.(0,)
C.(0,) D.(0,)
二、填空题(每小题5分,共35分)
8.函数y=中,自变量x的取值范围是________.
9.将一次函数y=3x-1的图像沿y轴向上平移3个单位长度后,得到的图像所对应的函数表达式为________.
10.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2__________0(填“>”或“<”).
11.已知一次函数y=(k-1)x|k|+3,则k=____________________________.
12.已知直线y=x+6与x轴、y轴围成一个三角形,则这个三角形的面积为________.
13.在直线y=x+1上,且到x轴或y轴的距离为2的点的坐标是________.
14.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为________.
三、解答题(共37分)
15.(10分)如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
16.(12分)某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号
载客量
租金单价
A
30人/辆
380元/辆
B
20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
(1)设租用A型号客车x辆,租车总费用为y元,求y与x的函数表达式,并写出x的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案最省钱?
17.(15分)从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5 km,下坡的速度比在平路上的速度每小时多5 km.设小明出发x h后,到达离甲地y km的地方,图6-Z-9中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为________km/h,他途中休息了________h;
(2)求线段AB,BC所表示的y与x之间的函数表达式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15 h,那么该地点离甲地多远?
答案
1.B.
2.D
3.C.
4 B.
5.A.
6. C
7. C.
8.x≤
9. y=3x+2.
10.>
11.-1.
12. 18.
13. (2,2)或(-2,0)或(-6,-2)
14.
15.解:(1)设直线l1的函数表达式为y=kx+b.
根据题意,得得
所以直线l1的函数表达式为y=-x+4.
(2)根据题意,得
解得
所以点B的坐标为(2,2).
16.解:(1)由题意得y=380x+280(62-x)=100x+17360.
∵30x+20(62-x)≥1441,
∴x≥20.1,∴21≤x≤62且x为整数.
(2)由题意得100x+17360≤21940,
解得x≤45.8,∴21≤x≤45且x为整数,
∴共有25种租车方案.
∵k=100>0,∴y随x的增大而增大.
当x=21时,y有最小值, y最小=100×21+17360=19460.
故共有25种租车方案,当租用A型号客车21辆,B型号客车41辆时,租金最少,为19460元.
17.解:(1)小明骑车在平路上的速度为4.5÷0.3=15(km/h),
∴小明骑车在上坡路上的速度为15-5=10(km/h),
小明骑车在下坡路上的速度为15+5=20(km/h),
∴小明从乙地返回甲地的时间为(6.5-4.5)÷20+0.3=0.4(h),
小明骑车到达乙地的时间为0.3+2÷10=0.5(h),
∴小明途中休息的时间为1-0.5-0.4=0.1(h).
故答案为15,0.1.
(2)小明骑车到达乙地的时间为0.5 h,
∴点B的坐标为(0.5,6.5).
小明下坡行驶的时间为2÷20=0.1(h),
∴点C的坐标为(0.6,4.5).
设线段AB所在直线的函数表达式为y=k1x+b1.
由题意,得
解得
∴线段AB所表示的y与x之间的函数表达式为y=10x+1.5(0.3≤x≤0.5).
设线段BC所在直线的函数表达式为y=k2x+b2.
由题意,得解得
∴线段BC所表示的y与x之间的函数表达式为y=-20x+16.5(0.5≤x≤0.6).
(3)小明两次经过途中某一地点的时间间隔为0.15 h,由题意可以得出这个地点只能在坡路上.设小明第一次经过该地点的时间为t h,则第二次经过该地点的时间为(t+0.15)h.由题意,得10t+1.5=-20(t+0.15)+16.5,解得t=0.4,
∴y=10×0.4+1.5=5.5.
答:该地点离甲地5.5 km.
一、选择题(每小题4分,共28分)
1.下列函数表达式:①y=-x;②y=3x+11;③y=x2+x+1;④y=. 其中属于一次函数的有( )
A.1个 B.2个 C.3个 D.4个
2.若点(m,n)在函数y=2x+1的图像上,则2m-n的值是( )
A.2 B.-2 C.1 D.-1
3.如图,直线l经过第一、二、四象限,l的函数表达式是y=(m-3)x+m+2,则m的取值范围在数轴上表示为( )
4.若实数a,b满足ab<0,则一次函数y=ax+b的图像可能是( )
5.如图,函数y=2x和y=ax+4的图像相交于点A(m,3),则不等式2x
6.如图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的函数关系图像.根据图像提供的信息,可知该公路的长度是( )
A.365米 B.500米 C.504米 D.684米
7.如图,在平面直角坐标系中,已知一次函数y=-x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A.(0,3) B.(0,)
C.(0,) D.(0,)
二、填空题(每小题5分,共35分)
8.函数y=中,自变量x的取值范围是________.
9.将一次函数y=3x-1的图像沿y轴向上平移3个单位长度后,得到的图像所对应的函数表达式为________.
10.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2__________0(填“>”或“<”).
11.已知一次函数y=(k-1)x|k|+3,则k=____________________________.
12.已知直线y=x+6与x轴、y轴围成一个三角形,则这个三角形的面积为________.
13.在直线y=x+1上,且到x轴或y轴的距离为2的点的坐标是________.
14.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为________.
三、解答题(共37分)
15.(10分)如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
16.(12分)某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号
载客量
租金单价
A
30人/辆
380元/辆
B
20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
(1)设租用A型号客车x辆,租车总费用为y元,求y与x的函数表达式,并写出x的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案最省钱?
17.(15分)从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5 km,下坡的速度比在平路上的速度每小时多5 km.设小明出发x h后,到达离甲地y km的地方,图6-Z-9中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为________km/h,他途中休息了________h;
(2)求线段AB,BC所表示的y与x之间的函数表达式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15 h,那么该地点离甲地多远?
答案
1.B.
2.D
3.C.
4 B.
5.A.
6. C
7. C.
8.x≤
9. y=3x+2.
10.>
11.-1.
12. 18.
13. (2,2)或(-2,0)或(-6,-2)
14.
15.解:(1)设直线l1的函数表达式为y=kx+b.
根据题意,得得
所以直线l1的函数表达式为y=-x+4.
(2)根据题意,得
解得
所以点B的坐标为(2,2).
16.解:(1)由题意得y=380x+280(62-x)=100x+17360.
∵30x+20(62-x)≥1441,
∴x≥20.1,∴21≤x≤62且x为整数.
(2)由题意得100x+17360≤21940,
解得x≤45.8,∴21≤x≤45且x为整数,
∴共有25种租车方案.
∵k=100>0,∴y随x的增大而增大.
当x=21时,y有最小值, y最小=100×21+17360=19460.
故共有25种租车方案,当租用A型号客车21辆,B型号客车41辆时,租金最少,为19460元.
17.解:(1)小明骑车在平路上的速度为4.5÷0.3=15(km/h),
∴小明骑车在上坡路上的速度为15-5=10(km/h),
小明骑车在下坡路上的速度为15+5=20(km/h),
∴小明从乙地返回甲地的时间为(6.5-4.5)÷20+0.3=0.4(h),
小明骑车到达乙地的时间为0.3+2÷10=0.5(h),
∴小明途中休息的时间为1-0.5-0.4=0.1(h).
故答案为15,0.1.
(2)小明骑车到达乙地的时间为0.5 h,
∴点B的坐标为(0.5,6.5).
小明下坡行驶的时间为2÷20=0.1(h),
∴点C的坐标为(0.6,4.5).
设线段AB所在直线的函数表达式为y=k1x+b1.
由题意,得
解得
∴线段AB所表示的y与x之间的函数表达式为y=10x+1.5(0.3≤x≤0.5).
设线段BC所在直线的函数表达式为y=k2x+b2.
由题意,得解得
∴线段BC所表示的y与x之间的函数表达式为y=-20x+16.5(0.5≤x≤0.6).
(3)小明两次经过途中某一地点的时间间隔为0.15 h,由题意可以得出这个地点只能在坡路上.设小明第一次经过该地点的时间为t h,则第二次经过该地点的时间为(t+0.15)h.由题意,得10t+1.5=-20(t+0.15)+16.5,解得t=0.4,
∴y=10×0.4+1.5=5.5.
答:该地点离甲地5.5 km.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
