11.2.2三角形的外角课件 (共28张PPT)
文档属性
| 名称 | 11.2.2三角形的外角课件 (共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 363.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-30 00:00:00 | ||
图片预览



文档简介
课件28张PPT。第十一章 三角形11.2 与三角形有关的角
第二课时 11.2.2 三角形的外角了解三角形的外角,并能在简单或复杂图形中辨别三角形的外角。
会利用三角形内角和定理,推出三个关于三角形外角的推论。
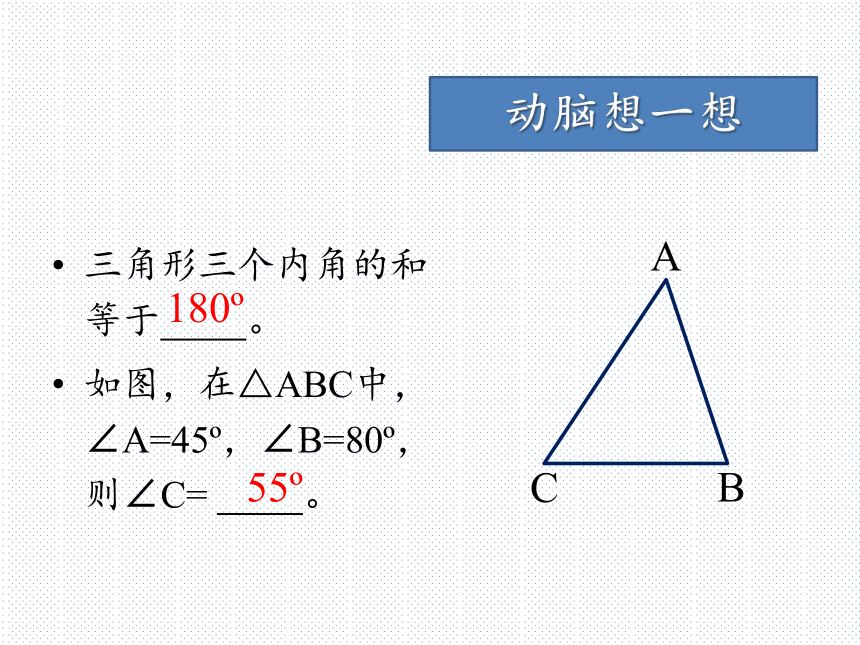
能根据三角形外角的相关性质解决实际问题。三角形三个内角的和等于 。
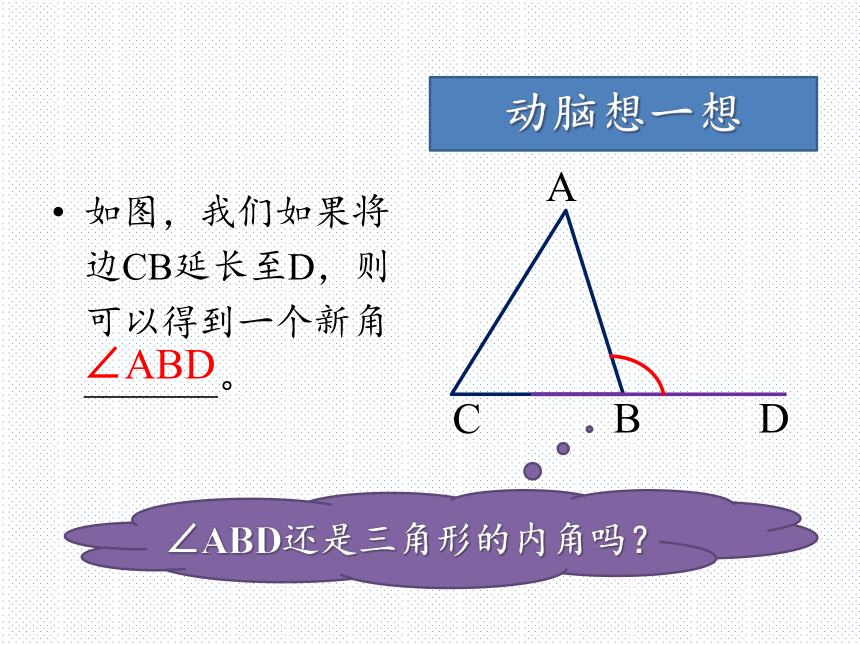
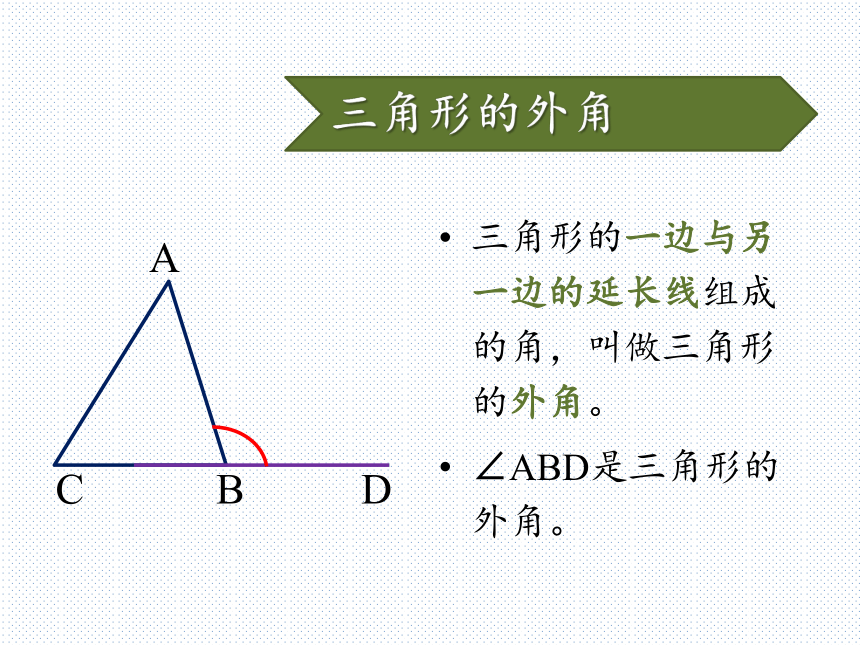
如图,在△ABC中,∠A=45o,∠B=80o,则∠C= 。动脑想一想180o55o如图,我们如果将边CB延长至D,则可以得到一个新角_______。动脑想一想D∠ABD∠ABD还是三角形的内角吗?三角形的外角三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
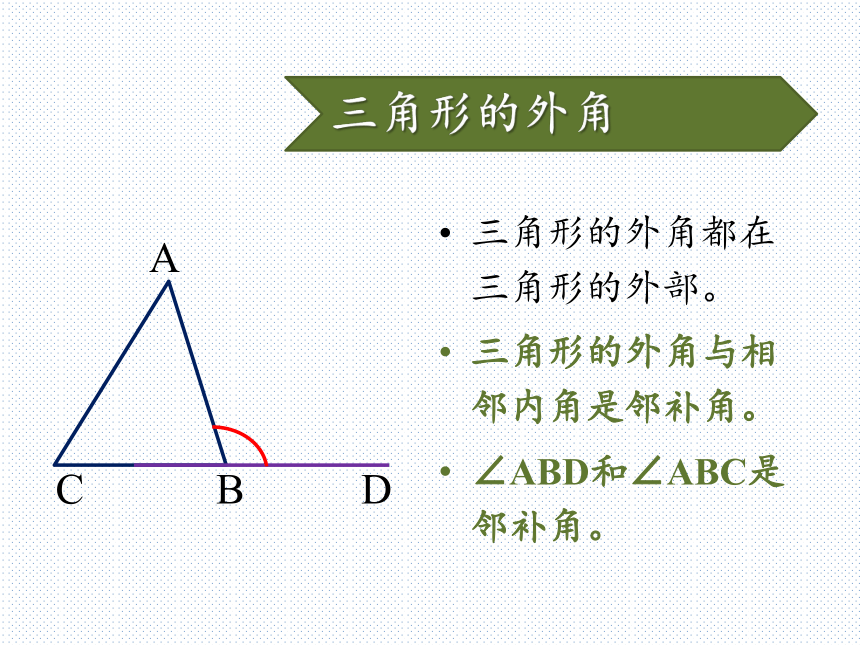
∠ABD是三角形的外角。D三角形的外角三角形的外角都在三角形的外部。
三角形的外角与相邻内角是邻补角。
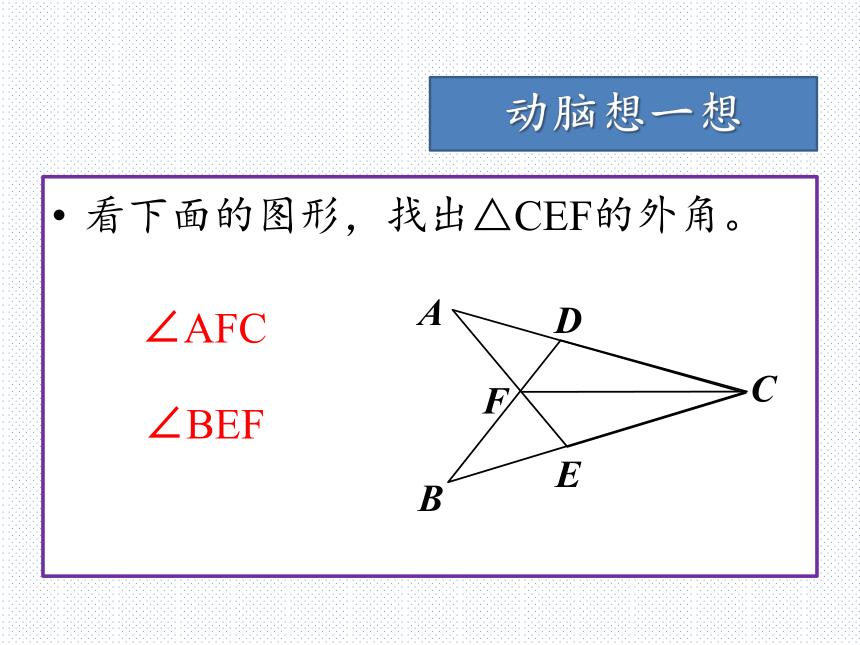
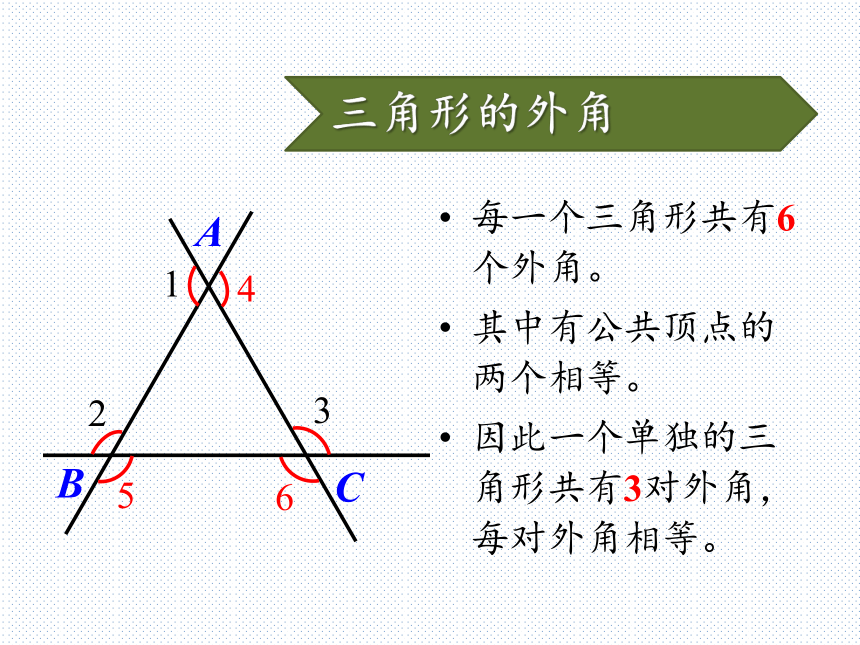
∠ABD和∠ABC是邻补角。D看下面的图形,找出△CEF的外角。动脑想一想∠AFC∠BEF动手做一做在纸上任意画一个△ABC,之后尝试画出它所有的外角(不重不漏)。一共能画出来多少个外角?试试看!三角形的外角每一个三角形共有6个外角。
其中有公共顶点的两个相等。
因此一个单独的三角形共有3对外角,每对外角相等。AB如图,在△ABC中,∠A=40o,∠C=65o,则∠ABC= _______。
∠ABD= 。
∠ABD= ∠A+∠C动脑想一想D75o你发现了什么规律?105o三角形外角的性质证明:
∵∠A + ∠ABC + ∠C=180o
并且∠ABD + ∠ABC=180o
∴∠ A + ∠C= ∠ABD
(等量代换)
D三角形的外角等于与它不相邻的两个内角的和。求下列图形中∠1的度数,并比较大小。动脑想一想∠1= o
∠1 120o ∠1= o
∠1 50o 85<95>三角形外角的性质∵∠ A + ∠C= ∠ABD
∴∠ABD>∠A
且∠ABD>∠C
D三角形的外角大于与它不相邻的任意一个内角。
看右面的五角星,思考下面的问题:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数和是多少?动脑想一想
解:
先看△AFC,可得:
∠A+ ∠C= ∠EFG
再看△BGD,可得:
∠B+ ∠D= ∠EGF
在△EFG中:
∠EGF + ∠EFG + ∠E = 180°
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
动脑想一想下列图形中,∠1+∠2+∠3= ?动脑想一想你能想到几种方法算出结果?三角形的外角和解法1:
∵∠1=∠ABC+∠ACB
∠2=∠BAC+∠ACB
∠3=∠BAC+∠ABC
∴∠1+∠2+∠3=2(∠ABC+∠BAC+∠ACB)
又∵ ∠ABC+∠BAC+∠ACB=180o
∴∠1+∠2+∠3=360o三角形的外角和解法2:
∵∠1+∠BAC=180o
∠2+∠ABC=180o
∠3+∠ACB=180o
∴∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540o
又∵ ∠ABC+∠BAC+∠ACB=180o
∴∠1+∠2+∠3=360o三角形的外角和解法3:
过A作AD平行于BC
∴∠3= ∠EAD
且∠2= ∠BAD
又∵∠1+∠EAD+∠BAD=360o
∴∠1+∠2+∠3=360oE三角形的外角和根据上面的不同种解法,你现在能够得出什么样的结论?三角形的三个不同顶点的外角的和等于360°学完本节课你应该知道三角形
的外角一个单独的三角形有3对两两相等的外角概念一边与另一边的延长线组成的角性质外角等于它不相邻的两个内角的和外角大于与它不相邻的任意一个内角三个不同顶点的外角的和等于360动笔练一练关于三角形的外角,下列说法中错误的是( )
A. 一个三角形有六个外角
B. 三角形的每个内角处都有两个外角
C. 三角形的每个外角是与它相邻内角的邻补角
D. 一个三角形只有三个外角D动笔练一练若三角形的一个外角等于它相邻的内角,则这个三角形是( );若一个外角小于与它相邻的锐角,则这个三角形是( )。
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 以上都有可能
BD动笔练一练比较下图中∠1、∠2和∠3的大小。∠1∠2∠3>>动笔练一练一个零件的形状如右图所示,按规定∠A应该等于90o,∠B和∠C分别是21o和20o,质量检验员测量后得到∠BDC=130o,直接判定该零件不合格,请说明原因。动笔练一练解:
延长CD交AB边于E点
则∠BDC=∠B+∠BED
且∠BED=∠C+∠A
∴∠BDC=∠A+∠B+∠C
=130o
因此该零件不合格课后练一练请同学们独立完成配套课后练习题下课!谢谢同学们!
第二课时 11.2.2 三角形的外角了解三角形的外角,并能在简单或复杂图形中辨别三角形的外角。
会利用三角形内角和定理,推出三个关于三角形外角的推论。
能根据三角形外角的相关性质解决实际问题。三角形三个内角的和等于 。
如图,在△ABC中,∠A=45o,∠B=80o,则∠C= 。动脑想一想180o55o如图,我们如果将边CB延长至D,则可以得到一个新角_______。动脑想一想D∠ABD∠ABD还是三角形的内角吗?三角形的外角三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
∠ABD是三角形的外角。D三角形的外角三角形的外角都在三角形的外部。
三角形的外角与相邻内角是邻补角。
∠ABD和∠ABC是邻补角。D看下面的图形,找出△CEF的外角。动脑想一想∠AFC∠BEF动手做一做在纸上任意画一个△ABC,之后尝试画出它所有的外角(不重不漏)。一共能画出来多少个外角?试试看!三角形的外角每一个三角形共有6个外角。
其中有公共顶点的两个相等。
因此一个单独的三角形共有3对外角,每对外角相等。AB如图,在△ABC中,∠A=40o,∠C=65o,则∠ABC= _______。
∠ABD= 。
∠ABD= ∠A+∠C动脑想一想D75o你发现了什么规律?105o三角形外角的性质证明:
∵∠A + ∠ABC + ∠C=180o
并且∠ABD + ∠ABC=180o
∴∠ A + ∠C= ∠ABD
(等量代换)
D三角形的外角等于与它不相邻的两个内角的和。求下列图形中∠1的度数,并比较大小。动脑想一想∠1= o
∠1 120o ∠1= o
∠1 50o 85<95>三角形外角的性质∵∠ A + ∠C= ∠ABD
∴∠ABD>∠A
且∠ABD>∠C
D三角形的外角大于与它不相邻的任意一个内角。
看右面的五角星,思考下面的问题:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数和是多少?动脑想一想
解:
先看△AFC,可得:
∠A+ ∠C= ∠EFG
再看△BGD,可得:
∠B+ ∠D= ∠EGF
在△EFG中:
∠EGF + ∠EFG + ∠E = 180°
∴∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
动脑想一想下列图形中,∠1+∠2+∠3= ?动脑想一想你能想到几种方法算出结果?三角形的外角和解法1:
∵∠1=∠ABC+∠ACB
∠2=∠BAC+∠ACB
∠3=∠BAC+∠ABC
∴∠1+∠2+∠3=2(∠ABC+∠BAC+∠ACB)
又∵ ∠ABC+∠BAC+∠ACB=180o
∴∠1+∠2+∠3=360o三角形的外角和解法2:
∵∠1+∠BAC=180o
∠2+∠ABC=180o
∠3+∠ACB=180o
∴∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540o
又∵ ∠ABC+∠BAC+∠ACB=180o
∴∠1+∠2+∠3=360o三角形的外角和解法3:
过A作AD平行于BC
∴∠3= ∠EAD
且∠2= ∠BAD
又∵∠1+∠EAD+∠BAD=360o
∴∠1+∠2+∠3=360oE三角形的外角和根据上面的不同种解法,你现在能够得出什么样的结论?三角形的三个不同顶点的外角的和等于360°学完本节课你应该知道三角形
的外角一个单独的三角形有3对两两相等的外角概念一边与另一边的延长线组成的角性质外角等于它不相邻的两个内角的和外角大于与它不相邻的任意一个内角三个不同顶点的外角的和等于360动笔练一练关于三角形的外角,下列说法中错误的是( )
A. 一个三角形有六个外角
B. 三角形的每个内角处都有两个外角
C. 三角形的每个外角是与它相邻内角的邻补角
D. 一个三角形只有三个外角D动笔练一练若三角形的一个外角等于它相邻的内角,则这个三角形是( );若一个外角小于与它相邻的锐角,则这个三角形是( )。
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 以上都有可能
BD动笔练一练比较下图中∠1、∠2和∠3的大小。∠1∠2∠3>>动笔练一练一个零件的形状如右图所示,按规定∠A应该等于90o,∠B和∠C分别是21o和20o,质量检验员测量后得到∠BDC=130o,直接判定该零件不合格,请说明原因。动笔练一练解:
延长CD交AB边于E点
则∠BDC=∠B+∠BED
且∠BED=∠C+∠A
∴∠BDC=∠A+∠B+∠C
=130o
因此该零件不合格课后练一练请同学们独立完成配套课后练习题下课!谢谢同学们!
