1.1.3 集合的基本运算31张PPT
文档属性
| 名称 | 1.1.3 集合的基本运算31张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-29 00:00:00 | ||
图片预览











文档简介
课件31张PPT。1.1.3 集合的基本运算
第1课时 并集、交集学校的文具店进货情况第一次与第二
次都进了哪几
种货物?两次
总共
进了
几种
货物? 两个实数除了可以比较大小外,还可以进行加减法运算.如果集合与实数相类比,我们会想集合是否也可以进行“加减”运算呢?
以上的例子就体现了集合间的运算,本节课就来研究这个问题.1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(重点)
2.能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.(重点)
3.能够利用交集、并集的性质解决一些简单问题. 观察下列各个集合,你能说出集合C与集合A,B之间的关系吗?(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}.集合C是由所有属于集合A或集合B的元素组成的.探究点1 并集集合间元素的关系 一般地,由所有属于集合A或属于集合B的元素
组成的集合,称为集合A与B的并集, 即:A∪B__________________.
用Venn图表示为:={x|x∈A,或x∈B}文字语言记作A∪B(读作“A并B”),符号语言图形语言1.两个集合的并集中的元素就是将两个集合中的元
素合在一起. ( )2.A∪B仍是一个集合,由所有属于集合A或属于
集合B的元素组成. ( )3.若集合A和集合B有公共元素,根据集合元素的互
异性,则在A∪B中仅出现一次. ( )×√√【即时训练】例1 设A={4,5,6,8}, B={3,5,7,8},
求A∪B.解: A∪B={4,5,6,8} ∪ {3,5,7,8}
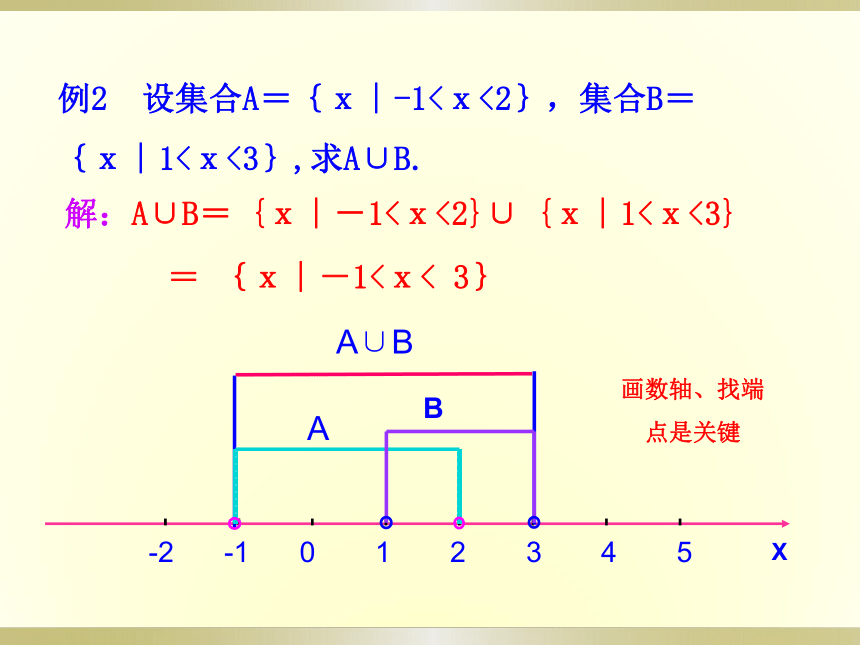
={3,4,5,6,7,8}元素全部拿过来,重复的只写一次【解题关键】例2 设集合A={x∣-1<x<2},集合B=
{x∣1<x<3},求A∪B.解:A∪B= {x∣-1<x<2}∪ {x∣1<x<3}A∪BAX = {x∣-1<x< 3}B画数轴、找端点是关键 两个集合求并集,结果还是一个集合,由集合A与B的所有元素组成的集合,它们的公共元素在并集中只能出现一次.对于表示不等式解集的集合的运算,可借助数轴解题.【提升总结】 ,求解: 本题通过数轴求得集合A与集合B的并集,思考在数轴上集合A与集合B的公共部分对应集合的什么运算呢?【互动探究】探究点2 交集上述三组集合中,集合A,B与集合C的关系如何?你能用Venn图表示出它们之间的关系吗?【解答】集合C中的元素既在集合A中,又在集合B中.各组集合均可用下图表示由图形可以看出:集合C中的每一个元素既在集合A中,又在集合B中。ACB交集 一般地,由属于集合A且属于集合B的所有元
素组成的集合,称为A与B的交集,记作A∩B(读作
“A交B”),即 A∩B=___________________.用Venn图表示为: {x|x∈A,且x∈B } 设集合A={1,2,3},集合B={-2,2},则
A∩B=( )
A.? B.{2}
C.{-2,2} D.{-2,1,2,3}B【解析】因为集合A={1,2,3},集合B={-2,2},所以A∩B={2}.【即时训练】例3 新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学},
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解:A∩B就是新华中学高一年级中那些既参加百米赛跑又参加跳高比赛的同学组成的集合.
所以,A∩B={x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}.例4 设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示l1,l2的位置关系.解:平面内直线l1,l2可能有三种位置关系,即相交于一点,平行或重合.
(1)直线l1,l2相交于一点P可表示为L1∩L2={点P};
(2)直线l1 ,l2平行可表示为L1∩ L2= ;
(3)直线l1 ,l2重合可表示为L1∩L2= L1=L2.【总结提升】 两个集合求交集,结果还是一个集合,由集合A与B的公共元素组成的集合,当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.(2)设集合A={x |1<x<5},集合B ={x|2<x
<6},求A B.(1)设集合A={4,5,6,8},集合B={3,5,
7,8,9},求A B.【变式练习】并集、交集的定义、表示及性质x∈A或x∈Bx∈A且x∈B=AA??===??【总结提升】1.如果A中有n个元素,B中有m个元素,那么A∪B中一定有m+n个元素吗?
提示:不一定.如果A∩B=?,A∪B中有m+n个元素.否则少于m+n个元素,若用符号card(A)表示A中的元素个数,则有card(A∪B)=card(A)+card(B)-card(A∩B).
2.A∩B与A∪B能否相等?
提示:可以相等.当A=B时,A∪B=A∩B.【易错点拨】例5 已知A={x|x≤4}, B={x|x>a},若A∪B=R,求实数a的取值范围.如图 a≤4.x已知A={x| a<x≤a+8},B={x|x<-1或x>5}.若A∪B=R,求a的取值范围.解:由A={x|a<x≤a+8},又B={x|x<-1或x>5},
在数轴上标出集合A,B的解集,如图.【变式练习】A3. 若集合A={1,2,3},B={1,3,4},则A∩B的子集个数为( )
A.2 B.3 C.4 D.16【解析】因为A={1,2,3},B={1,3,4}, 所以A∩B={1,3},则A∩B的子集个数为22=4. C4.设集合A={-1,0,1},B={a,a2},则使A∪B=A成立
的a的值为_____.
【解析】因为A∪B=A,所以B?A,
所以a2=0或a2=1,
所以a=0或a=±1,但a=0或a=1不符合条件,舍去,
故a=-1.-15、设集合A={-2},B={x|ax+1=0 a∈R},若A∩B=B,求a的值.【解析】 ∵A∩B=B,∴B?A.
∵A={-2}≠?,
∴B=?或B≠?. 两种方法几个性质并集与交集 两个定义 A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
A∩B=B∩A,A∪B=B∪A.数轴和Venn图.并集 A∪B={x|x∈A或x∈B},
交集 A∩B={x|x∈A且x∈B}. 追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他。
第1课时 并集、交集学校的文具店进货情况第一次与第二
次都进了哪几
种货物?两次
总共
进了
几种
货物? 两个实数除了可以比较大小外,还可以进行加减法运算.如果集合与实数相类比,我们会想集合是否也可以进行“加减”运算呢?
以上的例子就体现了集合间的运算,本节课就来研究这个问题.1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(重点)
2.能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.(重点)
3.能够利用交集、并集的性质解决一些简单问题. 观察下列各个集合,你能说出集合C与集合A,B之间的关系吗?(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}.集合C是由所有属于集合A或集合B的元素组成的.探究点1 并集集合间元素的关系 一般地,由所有属于集合A或属于集合B的元素
组成的集合,称为集合A与B的并集, 即:A∪B__________________.
用Venn图表示为:={x|x∈A,或x∈B}文字语言记作A∪B(读作“A并B”),符号语言图形语言1.两个集合的并集中的元素就是将两个集合中的元
素合在一起. ( )2.A∪B仍是一个集合,由所有属于集合A或属于
集合B的元素组成. ( )3.若集合A和集合B有公共元素,根据集合元素的互
异性,则在A∪B中仅出现一次. ( )×√√【即时训练】例1 设A={4,5,6,8}, B={3,5,7,8},
求A∪B.解: A∪B={4,5,6,8} ∪ {3,5,7,8}
={3,4,5,6,7,8}元素全部拿过来,重复的只写一次【解题关键】例2 设集合A={x∣-1<x<2},集合B=
{x∣1<x<3},求A∪B.解:A∪B= {x∣-1<x<2}∪ {x∣1<x<3}A∪BAX = {x∣-1<x< 3}B画数轴、找端点是关键 两个集合求并集,结果还是一个集合,由集合A与B的所有元素组成的集合,它们的公共元素在并集中只能出现一次.对于表示不等式解集的集合的运算,可借助数轴解题.【提升总结】 ,求解: 本题通过数轴求得集合A与集合B的并集,思考在数轴上集合A与集合B的公共部分对应集合的什么运算呢?【互动探究】探究点2 交集上述三组集合中,集合A,B与集合C的关系如何?你能用Venn图表示出它们之间的关系吗?【解答】集合C中的元素既在集合A中,又在集合B中.各组集合均可用下图表示由图形可以看出:集合C中的每一个元素既在集合A中,又在集合B中。ACB交集 一般地,由属于集合A且属于集合B的所有元
素组成的集合,称为A与B的交集,记作A∩B(读作
“A交B”),即 A∩B=___________________.用Venn图表示为: {x|x∈A,且x∈B } 设集合A={1,2,3},集合B={-2,2},则
A∩B=( )
A.? B.{2}
C.{-2,2} D.{-2,1,2,3}B【解析】因为集合A={1,2,3},集合B={-2,2},所以A∩B={2}.【即时训练】例3 新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学},
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解:A∩B就是新华中学高一年级中那些既参加百米赛跑又参加跳高比赛的同学组成的集合.
所以,A∩B={x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}.例4 设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示l1,l2的位置关系.解:平面内直线l1,l2可能有三种位置关系,即相交于一点,平行或重合.
(1)直线l1,l2相交于一点P可表示为L1∩L2={点P};
(2)直线l1 ,l2平行可表示为L1∩ L2= ;
(3)直线l1 ,l2重合可表示为L1∩L2= L1=L2.【总结提升】 两个集合求交集,结果还是一个集合,由集合A与B的公共元素组成的集合,当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.(2)设集合A={x |1<x<5},集合B ={x|2<x
<6},求A B.(1)设集合A={4,5,6,8},集合B={3,5,
7,8,9},求A B.【变式练习】并集、交集的定义、表示及性质x∈A或x∈Bx∈A且x∈B=AA??===??【总结提升】1.如果A中有n个元素,B中有m个元素,那么A∪B中一定有m+n个元素吗?
提示:不一定.如果A∩B=?,A∪B中有m+n个元素.否则少于m+n个元素,若用符号card(A)表示A中的元素个数,则有card(A∪B)=card(A)+card(B)-card(A∩B).
2.A∩B与A∪B能否相等?
提示:可以相等.当A=B时,A∪B=A∩B.【易错点拨】例5 已知A={x|x≤4}, B={x|x>a},若A∪B=R,求实数a的取值范围.如图 a≤4.x已知A={x| a<x≤a+8},B={x|x<-1或x>5}.若A∪B=R,求a的取值范围.解:由A={x|a<x≤a+8},又B={x|x<-1或x>5},
在数轴上标出集合A,B的解集,如图.【变式练习】A3. 若集合A={1,2,3},B={1,3,4},则A∩B的子集个数为( )
A.2 B.3 C.4 D.16【解析】因为A={1,2,3},B={1,3,4}, 所以A∩B={1,3},则A∩B的子集个数为22=4. C4.设集合A={-1,0,1},B={a,a2},则使A∪B=A成立
的a的值为_____.
【解析】因为A∪B=A,所以B?A,
所以a2=0或a2=1,
所以a=0或a=±1,但a=0或a=1不符合条件,舍去,
故a=-1.-15、设集合A={-2},B={x|ax+1=0 a∈R},若A∩B=B,求a的值.【解析】 ∵A∩B=B,∴B?A.
∵A={-2}≠?,
∴B=?或B≠?. 两种方法几个性质并集与交集 两个定义 A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
A∩B=B∩A,A∪B=B∪A.数轴和Venn图.并集 A∪B={x|x∈A或x∈B},
交集 A∩B={x|x∈A且x∈B}. 追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他。
