必修1 第三章函数的应用综合测试(含答案)
文档属性
| 名称 | 必修1 第三章函数的应用综合测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-30 15:00:27 | ||
图片预览




文档简介
必修1 函数的应用单元综合测试
一、单选题(每小题5分,共60分)
1.函数 的零点所在的区间为( )
A. (﹣1,0) B. (1,2) C. (0,1) D. (2,3)
2.函数的零点个数为( )
A. B. C. D.
3.若函数在区间内不是单调函数,则实数的取值范围是(??? )
A. B. C. D.
4.f(x)=ex﹣x﹣2在下列那个区间必有零点( )
A. (﹣1,0) B. (0,1) C. (1,2) D. (2,3)
5.函数的一个零点在区间内,则实数的取值范围是( )
A. B. C. D.
6.若函数的唯一零点同时在区间,,内,则下列命题中正确的是( )
A. 函数在区间内有零点 B. 函数在区间或内有零点
C. 函数在区间内无零点 D. 函数在区间内无零点
7.已知函数的图象是连续不断的曲线,且有如下对应值表,则函数在区间上的零点至少有(选最佳结果)( )
1
2
3
4
5
6
124.4
33
-74
24.5
-36.8
-122.6
A. 个 B. 个 C. 个 D. 个
8.设,若存在,使,则实数的取值范围是( )
A. B. C. 或 D.
9.若函数 的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:那么方程的一个近似根(精确到0.1)为( )
A. 1.2 B. 1.3 C. 1.4 D. 1.5
10.函数与图象交点的横坐标所在的区间是( )
A. B. C. D.
11.已知f(x)是定义在R上的奇函数,当x≥ 0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为( )
A. {1,3} B. {-3,-1,1,3}
C. {2-,1,3} D. {-2-,1,3}
12.若关于x的方程的一个根在区间内,另一个根在区间内,则实数的取值范围为
A. B. C. D.
二、填空题(每小题5分,共20分)
13.方程的实数解的个数为__________.
14.已知、两地相距千米,某人开汽车以千米/小时的速度从到达地,在地停留小时后再以千米/小时的速度返回地,把汽车离开地的距离表示为时间的函数,表达式为__________.
15.已知是方程的根, 是方程的根,则的值是______________.
16.定义一种运算,若,当有5个不同的零点时,则实数的取值范围是__________.
三、解答题(共70分)
17(10分).已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
18(12分).某商品每件成本元,售价元,每星期卖出件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值(单位:元,)成正比.已知商品降低元时,一星期多卖出件.
()将一星期的商品销售利润表示成的函数;
()如何定价才能使一个星期的商品销售利润最大,是多少?
19(12分).已知二次函数, 若, 且函数的值域为.
(1) 求函数的解析式;
(2) 若函数, 当时, 记的值域分别为,, 求实数的值.
20(12分).已知函数.
(Ⅰ)判断函数的奇偶性并求函数的零点;
(Ⅱ)写出的单调区间;(只需写出结果)
(Ⅲ)试讨论方程的根的情况.
21(12分).已知函数, ,设(其中表示中的较小者).
(1)在坐标系中画出函数的图像;
(2)设函数的最大值为,试判断与1的大小关系,并说明理由.
(参考数据: , , )
22(12分).已知函数为奇函数.
(1)求常数的值;
(2)设,证明函数在(1,+∞)上是减函数;
(3)若函数,且在区间[3,4]上没有零点,求实数的取值范围
参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
C
C
D
D
B
C
C
A
D
A
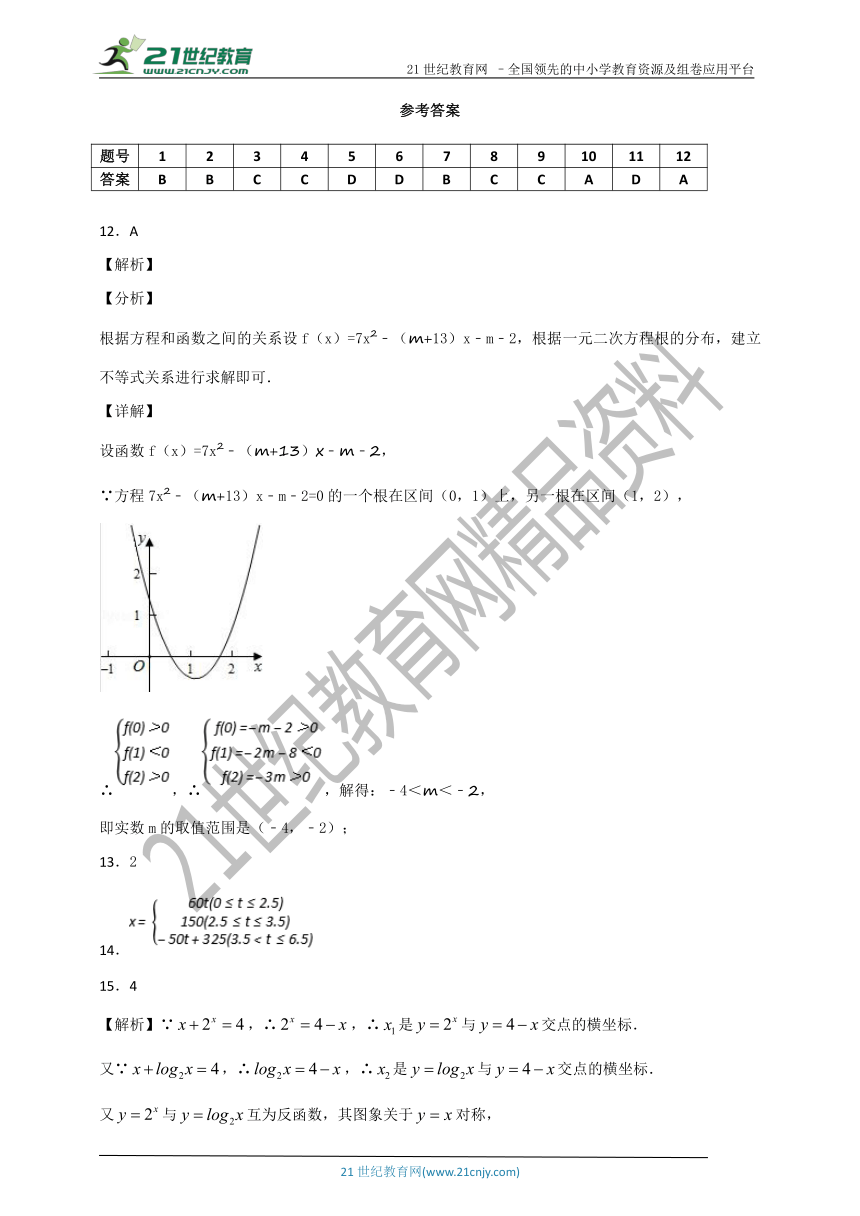
12.A
【解析】
【分析】
根据方程和函数之间的关系设f(x)=7x2﹣(m+13)x﹣m﹣2,根据一元二次方程根的分布,建立不等式关系进行求解即可.
【详解】
设函数f(x)=7x2﹣(m+13)x﹣m﹣2,
∵方程7x2﹣(m+13)x﹣m﹣2=0的一个根在区间(0,1)上,另一根在区间(1,2),
∴,∴,解得:﹣4<m<﹣2,
即实数m的取值范围是(﹣4,﹣2);
13.2
14.
15.4
【解析】∵,∴,∴是与交点的横坐标.
又∵,∴,∴是与交点的横坐标.
又与互为反函数,其图象关于对称,
由得,∴,∴.
16.
【解析】根据题意, ,画出其图象如图所示:
结合图象可以知道, 有5个零点时,实数m的取值范围是,
故答案为
17.(1)见解析.
(2)见解析.
(3) M={m|0【详解】
(1)当x2-4x+3≥0时,x≤1或x≥3,
∴f(x)=
∴f(x)的图象为:
(2)由函数的图象可知f(x)的单调区间是(-∞,1],(2,3),(1,2],[3,+∞),其中(-∞,1],(2,3)是减区间;(1,2],[3,+∞)是增区间.
(3)由f(x)的图象知,当018.(),();()定价为元时,利润最大为元.
【详解】
()由题意得,即每降价元,则多卖出件.
设总利润为元,
则
().
故销售利润表示成的函数为().
()由(1)得
.
所以当时,取得最大值元.
此时定价为元.
19.(1) ;(2)1.
【详解】
(1) 因为所以
因为函数的值域为
所以故.所以.
(2)当时,递增,可得最小值为,最大值为,
,
,当时,递增,可得最小值为,最大值为,
,
由,有,所以.
20.(Ⅰ)答案见解析;(Ⅱ)单调递增区间为;单调递减区间为(-1,1);(Ⅲ)答案见解析.
【解析】试题分析:
(Ⅰ)首先确定函数的定义域,然后结合可得为奇函数.
令,可得函数的零点为-2,0,2.
(Ⅱ)函数的单调递增区间为;单调递减区间为(-1,1).
(Ⅲ)结合函数的解析式绘制函数图象,观察图象可得:当或时,方程有一个根;当时,方程有两个根;当时,方程有三个根.
试题解析:
(Ⅰ)函数的定义域为R,关于坐标原点对称,
因为,
所以为奇函数.
令,即,
解得: ,
所以函数的零点为-2,0,2.
(Ⅱ)函数的单调递增区间为;单调递减区间为(-1,1).
(Ⅲ)由函数的解析式可得: ,
绘制函数图象如图所示,
观察函数图象可得:
当或时,方程有一个根;
当时,方程有两个根;
当时,方程有三个根.
21.(1)见解析;(2)见解析.
【解析】试题分析:(1)根据(其中表示中的较小者),即可画出函数的图像;(2)由题意可知, 为函数与图像交点的横坐标,即,设,根据零点存在定理及函数在上单调递增,且为连续曲线,可得有唯一零点,再由函数在上单调递减,即可得证.
试题解析:(1)作出函数的图像如下:
(2)由题意可知, 为函数与图像交点的横坐标,且,
∴.
设,易知即为函数的零点,
∵, ,
∴,
又∵函数在上单调递增,且为连续曲线,
∴有唯一零点
∵函数在上单调递减,
∴,即.
22.(1);(2)m>或m<-.
【解析】试题分析:(1)由于为奇函数,可得,即可得出;(2)利用对数函数的单调性和不等式的性质通过作差即可得出;(3)利用(2)函数的单调性、指数函数的单调性即可得出.
试题解析:∵f(x)=为奇函数
∴f(-x)=-f(x),即=-=,
∴,即1-k2x2=1-x2,整理得k2=1.
∴k=-1(k=1使f(x)无意义而舍去).
(2)证明:由(1)得,k=-1,h(x)=,任取x1,x2∈(1,+∞),且x1则h(x2)-h(x1)==.
∵x1,x2∈(1,+∞),且x1∴x1-x2<0,x1-1>0,x2-1>0,
∴h(x2)-h(x1)=,
∴h(x1)>h(x2),
∴函数y=h(x)在(1,+∞)是减函数.
(3)解:由(2)知,f(x)在(1,+∞)上递增,
∴g(x)=f(x)—+m在[3,4]递增.
∵g(x)在区间[3,4]上没有零点.
∴g(3)=-+m=+m>0或g(4)=-+m=, +m<0,
∴m>或m<-.
一、单选题(每小题5分,共60分)
1.函数 的零点所在的区间为( )
A. (﹣1,0) B. (1,2) C. (0,1) D. (2,3)
2.函数的零点个数为( )
A. B. C. D.
3.若函数在区间内不是单调函数,则实数的取值范围是(??? )
A. B. C. D.
4.f(x)=ex﹣x﹣2在下列那个区间必有零点( )
A. (﹣1,0) B. (0,1) C. (1,2) D. (2,3)
5.函数的一个零点在区间内,则实数的取值范围是( )
A. B. C. D.
6.若函数的唯一零点同时在区间,,内,则下列命题中正确的是( )
A. 函数在区间内有零点 B. 函数在区间或内有零点
C. 函数在区间内无零点 D. 函数在区间内无零点
7.已知函数的图象是连续不断的曲线,且有如下对应值表,则函数在区间上的零点至少有(选最佳结果)( )
1
2
3
4
5
6
124.4
33
-74
24.5
-36.8
-122.6
A. 个 B. 个 C. 个 D. 个
8.设,若存在,使,则实数的取值范围是( )
A. B. C. 或 D.
9.若函数 的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:那么方程的一个近似根(精确到0.1)为( )
A. 1.2 B. 1.3 C. 1.4 D. 1.5
10.函数与图象交点的横坐标所在的区间是( )
A. B. C. D.
11.已知f(x)是定义在R上的奇函数,当x≥ 0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为( )
A. {1,3} B. {-3,-1,1,3}
C. {2-,1,3} D. {-2-,1,3}
12.若关于x的方程的一个根在区间内,另一个根在区间内,则实数的取值范围为
A. B. C. D.
二、填空题(每小题5分,共20分)
13.方程的实数解的个数为__________.
14.已知、两地相距千米,某人开汽车以千米/小时的速度从到达地,在地停留小时后再以千米/小时的速度返回地,把汽车离开地的距离表示为时间的函数,表达式为__________.
15.已知是方程的根, 是方程的根,则的值是______________.
16.定义一种运算,若,当有5个不同的零点时,则实数的取值范围是__________.
三、解答题(共70分)
17(10分).已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
18(12分).某商品每件成本元,售价元,每星期卖出件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值(单位:元,)成正比.已知商品降低元时,一星期多卖出件.
()将一星期的商品销售利润表示成的函数;
()如何定价才能使一个星期的商品销售利润最大,是多少?
19(12分).已知二次函数, 若, 且函数的值域为.
(1) 求函数的解析式;
(2) 若函数, 当时, 记的值域分别为,, 求实数的值.
20(12分).已知函数.
(Ⅰ)判断函数的奇偶性并求函数的零点;
(Ⅱ)写出的单调区间;(只需写出结果)
(Ⅲ)试讨论方程的根的情况.
21(12分).已知函数, ,设(其中表示中的较小者).
(1)在坐标系中画出函数的图像;
(2)设函数的最大值为,试判断与1的大小关系,并说明理由.
(参考数据: , , )
22(12分).已知函数为奇函数.
(1)求常数的值;
(2)设,证明函数在(1,+∞)上是减函数;
(3)若函数,且在区间[3,4]上没有零点,求实数的取值范围
参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
C
C
D
D
B
C
C
A
D
A
12.A
【解析】
【分析】
根据方程和函数之间的关系设f(x)=7x2﹣(m+13)x﹣m﹣2,根据一元二次方程根的分布,建立不等式关系进行求解即可.
【详解】
设函数f(x)=7x2﹣(m+13)x﹣m﹣2,
∵方程7x2﹣(m+13)x﹣m﹣2=0的一个根在区间(0,1)上,另一根在区间(1,2),
∴,∴,解得:﹣4<m<﹣2,
即实数m的取值范围是(﹣4,﹣2);
13.2
14.
15.4
【解析】∵,∴,∴是与交点的横坐标.
又∵,∴,∴是与交点的横坐标.
又与互为反函数,其图象关于对称,
由得,∴,∴.
16.
【解析】根据题意, ,画出其图象如图所示:
结合图象可以知道, 有5个零点时,实数m的取值范围是,
故答案为
17.(1)见解析.
(2)见解析.
(3) M={m|0
(1)当x2-4x+3≥0时,x≤1或x≥3,
∴f(x)=
∴f(x)的图象为:
(2)由函数的图象可知f(x)的单调区间是(-∞,1],(2,3),(1,2],[3,+∞),其中(-∞,1],(2,3)是减区间;(1,2],[3,+∞)是增区间.
(3)由f(x)的图象知,当0
【详解】
()由题意得,即每降价元,则多卖出件.
设总利润为元,
则
().
故销售利润表示成的函数为().
()由(1)得
.
所以当时,取得最大值元.
此时定价为元.
19.(1) ;(2)1.
【详解】
(1) 因为所以
因为函数的值域为
所以故.所以.
(2)当时,递增,可得最小值为,最大值为,
,
,当时,递增,可得最小值为,最大值为,
,
由,有,所以.
20.(Ⅰ)答案见解析;(Ⅱ)单调递增区间为;单调递减区间为(-1,1);(Ⅲ)答案见解析.
【解析】试题分析:
(Ⅰ)首先确定函数的定义域,然后结合可得为奇函数.
令,可得函数的零点为-2,0,2.
(Ⅱ)函数的单调递增区间为;单调递减区间为(-1,1).
(Ⅲ)结合函数的解析式绘制函数图象,观察图象可得:当或时,方程有一个根;当时,方程有两个根;当时,方程有三个根.
试题解析:
(Ⅰ)函数的定义域为R,关于坐标原点对称,
因为,
所以为奇函数.
令,即,
解得: ,
所以函数的零点为-2,0,2.
(Ⅱ)函数的单调递增区间为;单调递减区间为(-1,1).
(Ⅲ)由函数的解析式可得: ,
绘制函数图象如图所示,
观察函数图象可得:
当或时,方程有一个根;
当时,方程有两个根;
当时,方程有三个根.
21.(1)见解析;(2)见解析.
【解析】试题分析:(1)根据(其中表示中的较小者),即可画出函数的图像;(2)由题意可知, 为函数与图像交点的横坐标,即,设,根据零点存在定理及函数在上单调递增,且为连续曲线,可得有唯一零点,再由函数在上单调递减,即可得证.
试题解析:(1)作出函数的图像如下:
(2)由题意可知, 为函数与图像交点的横坐标,且,
∴.
设,易知即为函数的零点,
∵, ,
∴,
又∵函数在上单调递增,且为连续曲线,
∴有唯一零点
∵函数在上单调递减,
∴,即.
22.(1);(2)m>或m<-.
【解析】试题分析:(1)由于为奇函数,可得,即可得出;(2)利用对数函数的单调性和不等式的性质通过作差即可得出;(3)利用(2)函数的单调性、指数函数的单调性即可得出.
试题解析:∵f(x)=为奇函数
∴f(-x)=-f(x),即=-=,
∴,即1-k2x2=1-x2,整理得k2=1.
∴k=-1(k=1使f(x)无意义而舍去).
(2)证明:由(1)得,k=-1,h(x)=,任取x1,x2∈(1,+∞),且x1
∵x1,x2∈(1,+∞),且x1
∴h(x2)-h(x1)=,
∴h(x1)>h(x2),
∴函数y=h(x)在(1,+∞)是减函数.
(3)解:由(2)知,f(x)在(1,+∞)上递增,
∴g(x)=f(x)—+m在[3,4]递增.
∵g(x)在区间[3,4]上没有零点.
∴g(3)=-+m=+m>0或g(4)=-+m=, +m<0,
∴m>或m<-.
