向心加速度课件(共35张PPT)
文档属性
| 名称 | 向心加速度课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 734.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-08-30 15:25:52 | ||
图片预览







文档简介
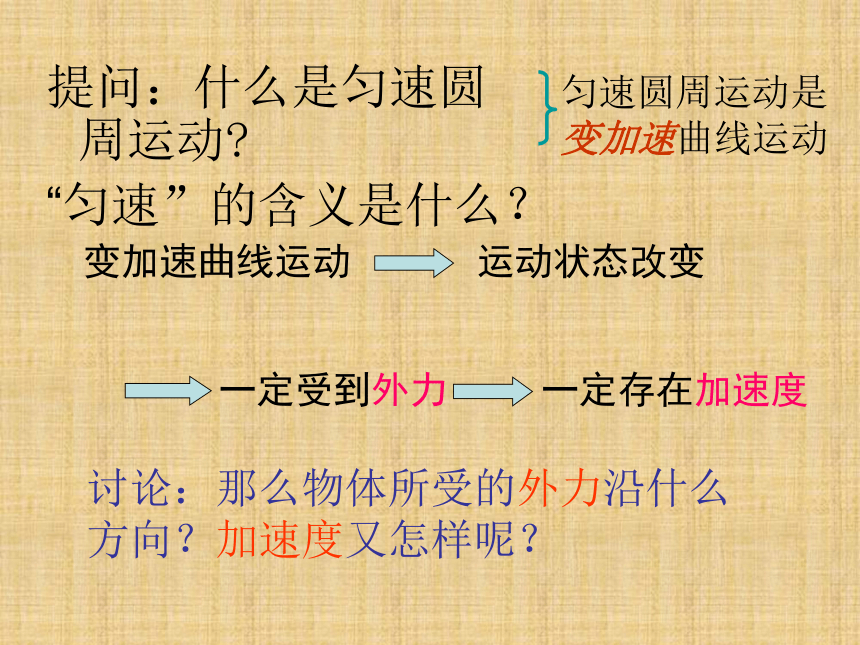
课件35张PPT。5.5 向心加速度提问:什么是匀速圆周运动?
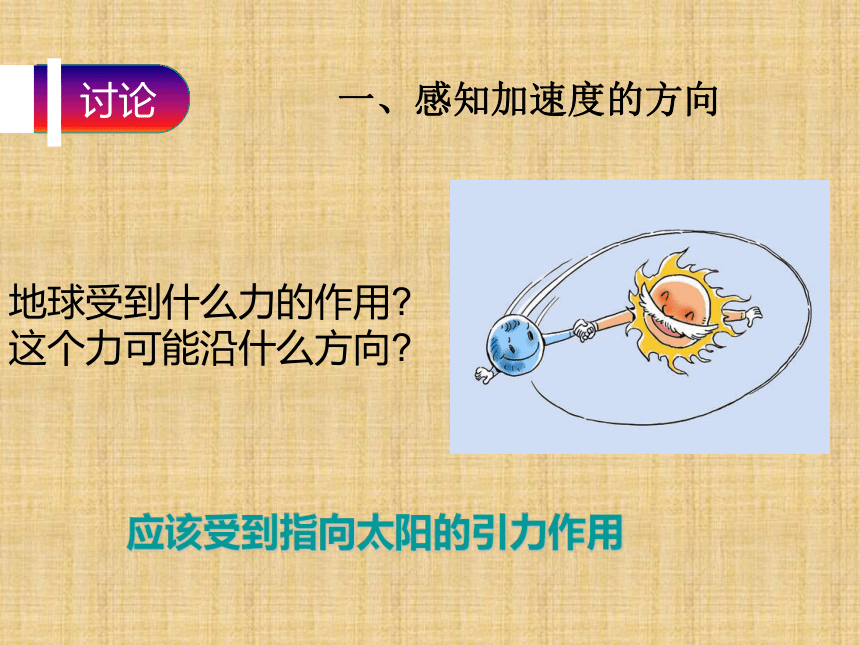
“匀速”的含义是什么?讨论:那么物体所受的外力沿什么方向?加速度又怎样呢?匀速圆周运动是变加速曲线运动变加速曲线运动运动状态改变一定受到外力一定存在加速度 通过前面的学习,我们已经知道,做曲线运动的物体速度一定是变化的.即使是我们上一堂课研究的匀速圆周运动,其方向仍在不断变化着.换句话说,做曲线运动的物体,一定有加速度.圆周运动是曲线运动,那么做圆周运动的物体,加速度的大小和方向如何确定呢?——这就是我们今天要研究的课题. 地球受到什么力的作用?
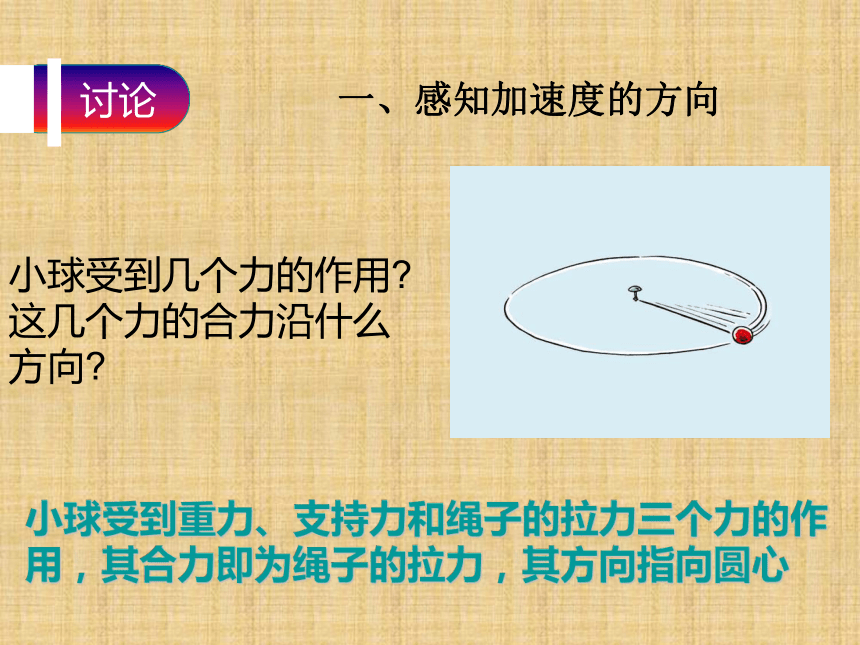
这个力可能沿什么方向? 一、感知加速度的方向 应该受到指向太阳的引力作用 小球受到几个力的作用?
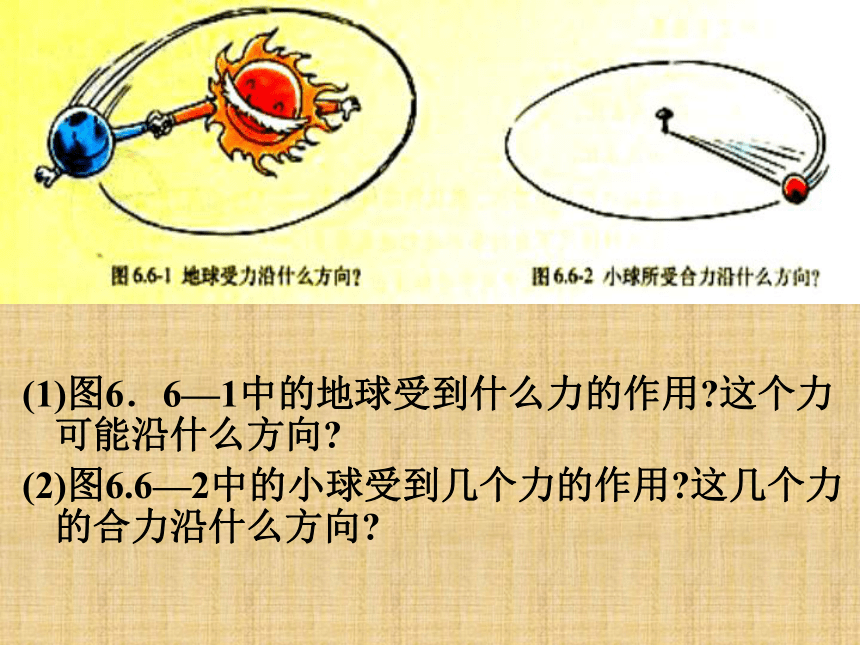
这几个力的合力沿什么方向? 小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心 一、感知加速度的方向 (1)图6.6—1中的地球受到什么力的作用?这个力可能沿什么方向?
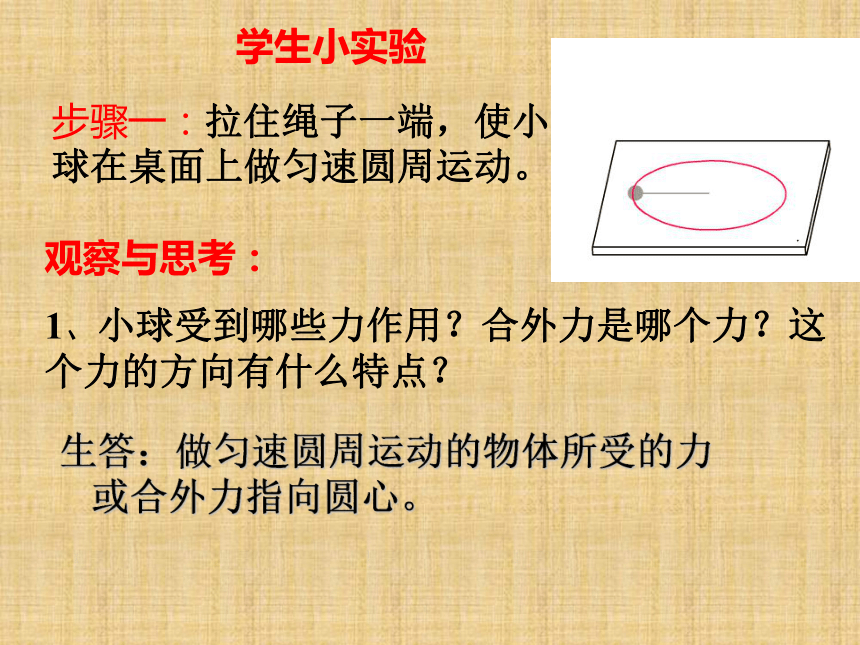
(2)图6.6—2中的小球受到几个力的作用?这几个力的合力沿什么方向?学生小实验步骤一:拉住绳子一端,使小球在桌面上做匀速圆周运动。观察与思考:
1、小球受到哪些力作用?合外力是哪个力?这个力的方向有什么特点?生答:做匀速圆周运动的物体所受的力或合外力指向圆心。2、我们这节课讨论向心加速度,而这里却在讨论物体受力情况,这不是“南辕北辙”了吗?生答:由牛顿第二定律知,知道了合外力就可以推出加速度,那么物体的加速度也指向圆心3、“任何物体做匀速圆周运动的加速度都指向圆心”吗? 我们这节课要研究的是匀速圆周运动的加速度,可是以上两个例题却在研究物体所受的力,这不是“南辕北辙”了吗? 一、感知加速度的方向 在刚才的研究中,同学们已充分感知了做匀速圆周运动的物体所受的力或合外力指向圆心,所以物体的加速度也指向圆心.是不是由此可以得出结论:“任何物体做匀速圆周运动的加速度都指向圆心”?暂时不能,因为上面只研究了有限的实例.还难以得出一般性的结论.然而,这样的研究十分有益,因为它强烈地向我们提示了问题的答案,给我们指出了方向.一、感知加速度的方向 速度的变化量△v是矢量还是标量?
如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v? (1)在A、B两点画速度矢量vA和vB时,要注意什么?
(2)将vA的起点移到B点时要注意什么?
(3)如何画出质点由A点运动到B点时速度的变化量△V?
(4)△v/△t表示的意义是什么?
(5)△v与圆的半径平行吗?在什么条件下.△v与圆的半径平行?分析生活中圆周运动例子: 下面我们要从加速度的定义a= △ v/△t进行一般性的讨论一、速度的变化量1、如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v? △v是矢量还是标量?甲V1△VV2(1)v1 < V2 (如图甲)乙V1△VV2(2)v1 > v2 (如图乙)2、如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?V1△VV2在图6.6—6丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的?三、向心加速度上面的推导不涉及“地球公转“小球绕图钉转动”等具体的运动,结论具有一般性:做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.三、向心加速度的方向an=v2/r , an=rω2 三、向心加速度的大小按照课本第5l页“做一做”栏目中的提示,在练习本上推导出向心加速度的表达式 速度的变化量△v与初速度v1和末速度v2的关系:从同一点作出物体在一段时间的始末两个速度的矢量v1和v 2,从初速度矢量v1的末端作一个矢量△v至末速度矢量v2的末端,矢量△v就等于速度的变化量。速度的变化量探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为VA,经过时间后位于B点,速度为VB,质点速度的变化量沿什么方向?注意:1、 VA 、VB的长度是否一样?2、VA平移时注意什么?3、△v/△t表示什么?4、△v与圆的半径平行吗?在什么条件下,△v与圆的半径平行?结论:当△t很小很小时,△v指向圆心. 二、向心加速度1、做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度. △vV△Lra= △ v/△tV = △ L /△t思考:从公式a=v2/r看,向心加速度与圆周运动的半径成反比;从公式a=rw2看,向心加速度与半径成正比,这两个结论是否矛盾?1)在y=kx这个关系式中,说y与x成正比,前提是什么?2)自行车的大齿轮、小齿轮、后轮三个轮子的 半径不一样,它们的边缘上有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径 成正比”,哪两点适用于“向心加速度与半径 成反比”? 实验方法——控制因素(变量)法1.F与m的关系2.F与r的关系3.F与ω的关系结论: F ∝m结论: F ∝ r结论: F ∝ ω25、向心力的大小①、当r、ω一定时,向心力与质 量成正比②、当m、r一定时,角速度越大,
向心力越大③、当m、ω一定时,运动半径
越大,向心力越大2、向心力的大小:F = mrω2F = mv2/r角速度一定时,向心力与半径成正比线速度一定时,向心力与半径成反比二、向心加速度1、向心加速度即向心力产生的加速度,只是描述线速度方向变化的快慢。大小: a = F/m=?
a= rω2 a= v2/r
方向: 与向心力方向一致,即总指向圆心,向心加速度的方向是不断变化的。2、匀速圆周运动的性质:加速度大小不变,方向时刻改变,是变加速运动.三、课堂练习1、下列关于向心加速度的说法中,正确的是…………( )
A.向心加速度的方向始终与速度的方向垂直
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
2、一个拖拉机后轮直径是前轮直径的2倍,当前进且不打滑时,前轮边缘上某点A的线速度与后轮边缘上某点B的线速度之比VA:VB=________,
角速度之比ωA:ωB=_________,
向心加速度之比aA:aB=_________。1 、科学方法:
(1)发现物理规律的基本方法:以观察实验为基础,分析、综合的方法;
(2)实验方法:研究物理问题的重要方法之一——控制因素(变量)法。2、 知识整合:圆周运动匀速圆
周运动匀速圆
周运动圆周运动 向心力
(向心加速度)再见
“匀速”的含义是什么?讨论:那么物体所受的外力沿什么方向?加速度又怎样呢?匀速圆周运动是变加速曲线运动变加速曲线运动运动状态改变一定受到外力一定存在加速度 通过前面的学习,我们已经知道,做曲线运动的物体速度一定是变化的.即使是我们上一堂课研究的匀速圆周运动,其方向仍在不断变化着.换句话说,做曲线运动的物体,一定有加速度.圆周运动是曲线运动,那么做圆周运动的物体,加速度的大小和方向如何确定呢?——这就是我们今天要研究的课题. 地球受到什么力的作用?
这个力可能沿什么方向? 一、感知加速度的方向 应该受到指向太阳的引力作用 小球受到几个力的作用?
这几个力的合力沿什么方向? 小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心 一、感知加速度的方向 (1)图6.6—1中的地球受到什么力的作用?这个力可能沿什么方向?
(2)图6.6—2中的小球受到几个力的作用?这几个力的合力沿什么方向?学生小实验步骤一:拉住绳子一端,使小球在桌面上做匀速圆周运动。观察与思考:
1、小球受到哪些力作用?合外力是哪个力?这个力的方向有什么特点?生答:做匀速圆周运动的物体所受的力或合外力指向圆心。2、我们这节课讨论向心加速度,而这里却在讨论物体受力情况,这不是“南辕北辙”了吗?生答:由牛顿第二定律知,知道了合外力就可以推出加速度,那么物体的加速度也指向圆心3、“任何物体做匀速圆周运动的加速度都指向圆心”吗? 我们这节课要研究的是匀速圆周运动的加速度,可是以上两个例题却在研究物体所受的力,这不是“南辕北辙”了吗? 一、感知加速度的方向 在刚才的研究中,同学们已充分感知了做匀速圆周运动的物体所受的力或合外力指向圆心,所以物体的加速度也指向圆心.是不是由此可以得出结论:“任何物体做匀速圆周运动的加速度都指向圆心”?暂时不能,因为上面只研究了有限的实例.还难以得出一般性的结论.然而,这样的研究十分有益,因为它强烈地向我们提示了问题的答案,给我们指出了方向.一、感知加速度的方向 速度的变化量△v是矢量还是标量?
如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v? (1)在A、B两点画速度矢量vA和vB时,要注意什么?
(2)将vA的起点移到B点时要注意什么?
(3)如何画出质点由A点运动到B点时速度的变化量△V?
(4)△v/△t表示的意义是什么?
(5)△v与圆的半径平行吗?在什么条件下.△v与圆的半径平行?分析生活中圆周运动例子: 下面我们要从加速度的定义a= △ v/△t进行一般性的讨论一、速度的变化量1、如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v? △v是矢量还是标量?甲V1△VV2(1)v1 < V2 (如图甲)乙V1△VV2(2)v1 > v2 (如图乙)2、如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?V1△VV2在图6.6—6丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的?三、向心加速度上面的推导不涉及“地球公转“小球绕图钉转动”等具体的运动,结论具有一般性:做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.三、向心加速度的方向an=v2/r , an=rω2 三、向心加速度的大小按照课本第5l页“做一做”栏目中的提示,在练习本上推导出向心加速度的表达式 速度的变化量△v与初速度v1和末速度v2的关系:从同一点作出物体在一段时间的始末两个速度的矢量v1和v 2,从初速度矢量v1的末端作一个矢量△v至末速度矢量v2的末端,矢量△v就等于速度的变化量。速度的变化量探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为VA,经过时间后位于B点,速度为VB,质点速度的变化量沿什么方向?注意:1、 VA 、VB的长度是否一样?2、VA平移时注意什么?3、△v/△t表示什么?4、△v与圆的半径平行吗?在什么条件下,△v与圆的半径平行?结论:当△t很小很小时,△v指向圆心. 二、向心加速度1、做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度. △vV△Lra= △ v/△tV = △ L /△t思考:从公式a=v2/r看,向心加速度与圆周运动的半径成反比;从公式a=rw2看,向心加速度与半径成正比,这两个结论是否矛盾?1)在y=kx这个关系式中,说y与x成正比,前提是什么?2)自行车的大齿轮、小齿轮、后轮三个轮子的 半径不一样,它们的边缘上有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径 成正比”,哪两点适用于“向心加速度与半径 成反比”? 实验方法——控制因素(变量)法1.F与m的关系2.F与r的关系3.F与ω的关系结论: F ∝m结论: F ∝ r结论: F ∝ ω25、向心力的大小①、当r、ω一定时,向心力与质 量成正比②、当m、r一定时,角速度越大,
向心力越大③、当m、ω一定时,运动半径
越大,向心力越大2、向心力的大小:F = mrω2F = mv2/r角速度一定时,向心力与半径成正比线速度一定时,向心力与半径成反比二、向心加速度1、向心加速度即向心力产生的加速度,只是描述线速度方向变化的快慢。大小: a = F/m=?
a= rω2 a= v2/r
方向: 与向心力方向一致,即总指向圆心,向心加速度的方向是不断变化的。2、匀速圆周运动的性质:加速度大小不变,方向时刻改变,是变加速运动.三、课堂练习1、下列关于向心加速度的说法中,正确的是…………( )
A.向心加速度的方向始终与速度的方向垂直
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
2、一个拖拉机后轮直径是前轮直径的2倍,当前进且不打滑时,前轮边缘上某点A的线速度与后轮边缘上某点B的线速度之比VA:VB=________,
角速度之比ωA:ωB=_________,
向心加速度之比aA:aB=_________。1 、科学方法:
(1)发现物理规律的基本方法:以观察实验为基础,分析、综合的方法;
(2)实验方法:研究物理问题的重要方法之一——控制因素(变量)法。2、 知识整合:圆周运动匀速圆
周运动匀速圆
周运动圆周运动 向心力
(向心加速度)再见
