28.1.3 二次函数y=ax2+bx+c的图像性质同步课时作业(2)
文档属性
| 名称 | 28.1.3 二次函数y=ax2+bx+c的图像性质同步课时作业(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-31 00:00:00 | ||
图片预览




文档简介
28.1.3二次函数y=ax2+bx+c的图像性质同步课时作业(2)
姓名:__________班级:__________考号:__________
一、选择题
1.把二次函数y=x2﹣4x+1化成y=a(x+m)2+k的形式是( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
2.已知二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的表达式为( )
A. y=-3x2-1 B. y=3x2 C. y=3x2+1 D. y=3x2-1
3.把抛物线向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
A. B. C. D.
4.二次函数的图象经过三点,则它的解析式为
A. B.
C. D.
5.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y=(x﹣2)2+3 B. y=(x﹣2)2﹣3
C. y=﹣(x﹣2)2+3 D. y=﹣(x﹣2)2﹣3
6.将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
A.b>8 B.b>﹣8 C.b≥8 D.b≥﹣8
7.对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x 2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x 2﹣8x+2
8.若二次函数的图象经过点(2,0),且其对称轴为,则使函数值成立的的取值范围是( )
A.或 B.≤ ≤ C.≤或≥ D.
二、填空题
9.与抛物线关于轴对称的抛物线解析式是__________.
10.一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为_______.
11.抛物线y=ax2+bx+c中,已知a:b:c=1:2:3,y最小值为6,则此抛物线的解析式为_______.
12.请写出一个图象的对称轴为y轴,开口向下,且经过点(1,﹣2)的二次函数解析式,这个二次函数的解析式可以是_____.
13.如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
14.邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据
1
2
3
4
5
6
…
输出数据
…
那么,当输入数据是7时,输出的数据是 .
三、解答题
15.已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
16.已知抛物线y=x2﹣4x+3.
(1)用配方法将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该抛物线的对称轴和顶点坐标;
(3)直接写出当x满足什么条件时,函数y<0.
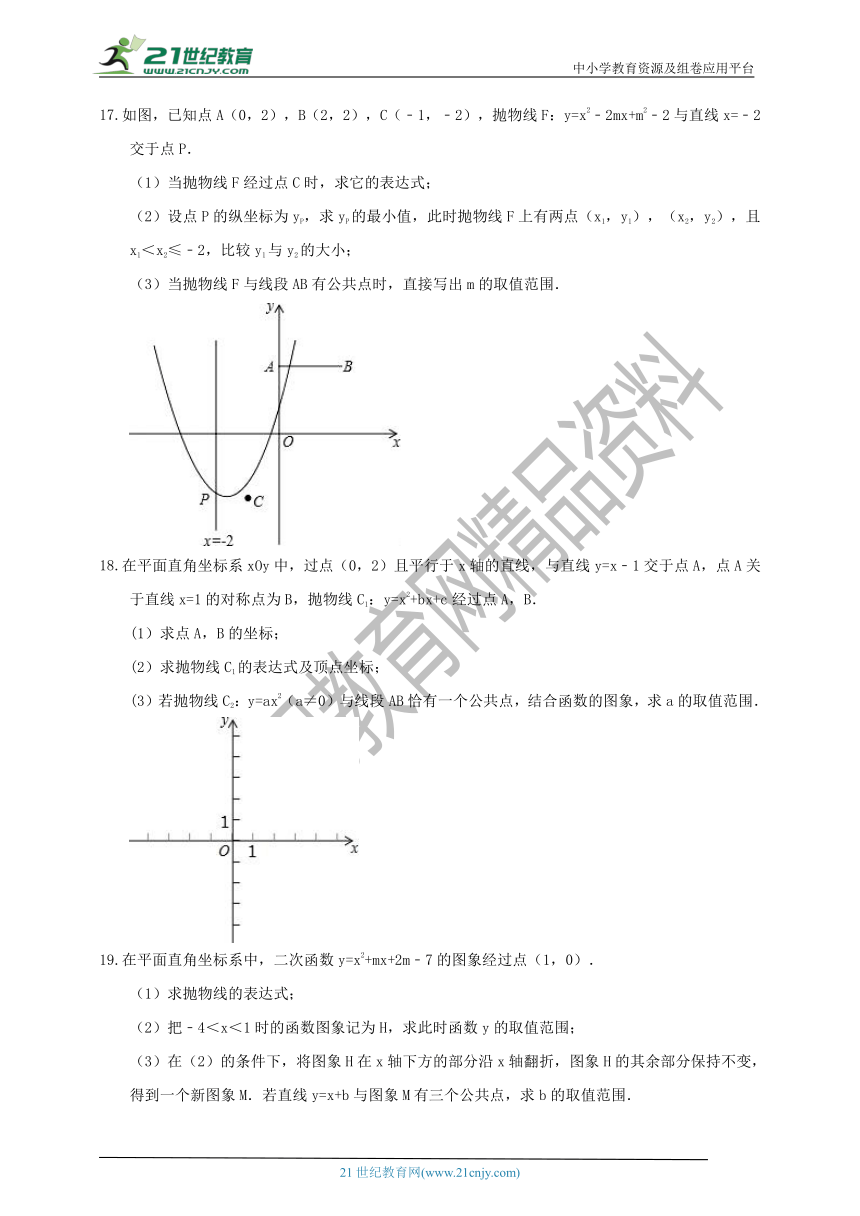
17.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
18.在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x﹣1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
19.在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
答案解析
一 、选择题
1.【考点】二次函数的三种形式.
【分析】运用配方法把二次函数的一般式化为顶点式即可.
解:y=x2﹣4x+1
=x2﹣4x+4﹣3
=(x﹣2)2﹣3,
故选:D.
2.D
【解析】∵二次函数图象的顶点坐标为(0,1),图象与轴的交点坐标为和,
∴二次函数图象沿轴翻折后的抛物线的顶坐标为(0,-1),与轴的交点坐标为和,
∴可设新抛物线的表达式为:,代入点可得:,解得,
∴翻折后所得抛物线的表达式为:.
故选D.
点睛:抛物线沿轴翻折后所得新的抛物线表达式为.
3.D
【解析】
试题【分析】根据抛物线的平移规律可得:把抛物线向下平移2个单位,得,再向右平移1个单位,所得到的抛物线是,故选:D.
【考点】抛物线的平移.
4.D
【解析】设该二次函数的解析式为:,则由已知条件可得:
,解得: ,
∴该二次函数的解析式为:.
故选D.
5.C
【解析】抛物线开口向下,顶点是(2,3),所以y=﹣(x﹣2)2+3,选C.
点睛:
求二次函数的解析式
(1)已知二次函数过三个点,利用一般式,y=ax2+bx+c().列方程组求二次函数解析式.
(2)已知二次函数与x轴的两个交点 (,利用双根式,y= ()求二次函数解析式,而且此时对称轴方程过交点的中点, .
(3)已知二次函数的顶点坐标,利用顶点式,()求二次函数解析式.
其中a决定开始方向和大小,顶点坐标是(h,k),对称轴方程是x=h.
(4)已知条件中a,b,c,给定了一个值,则需要列两个方程求解.
(5)已知条件有对称轴,对称轴也可以作为一个方程;如果给定的两个点纵坐标相同 (,则可以得到对称轴方程.
6.【考点】二次函数图象与几何变换;一次函数图象与系数的关系.
【分析】先根据平移原则:上→加,下→减,左→加,右→减写出解析式,再列方程组,有公共点则△≥0,则可求出b的取值.
解:由题意得:平移后得到的二次函数的解析式为:y=(x﹣3)2﹣1,
则,
(x﹣3)2﹣1=2x+b,
x2﹣8x+8﹣b=0,
△=(﹣8)2﹣4×1×(8﹣b)≥0,
b≥﹣8,
故选D.
7.C
【解析】根据题意,设y=a(x?2)2+3,抛物线经过点(3,1),所以a+3=1,a=?2.
因此抛物线的解析式为:y=?2(x?2)2+3=?2x2+8x?5.
故选:C.
8.【考点】二次函数与不等式(组)..
【分析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
二 、填空题
9.
【解析】【分析】把原抛物线解析式转化为顶点式形式,求出顶点坐标,再根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求出描出的抛物线的顶点坐标,然后根据描出的抛物线与原抛物线形状相同,开口方向向下写出解析式即可.
详解:∵,
∴顶点,
∴顶点关于轴,对称点为且开口向下,
∴.
故答案为:.
点睛:此题主要考查了二次函数的图像与性质,关键是求出关键点—顶点的对称坐标,然后根据对称性求出函数的解析式,是常考题.
10.y=﹣2(x+1)2+3 或y=-2x2-4x+1
【解析】由题意可知:该抛物线的解析式为y=?2(x?h)2+k,
又∵顶点坐标(?1,3),
∴y=?2(x+1)2+3=-2x2-4x+1,
故答案为:y=﹣2(x+1)2+3 或y=-2x2-4x+1.
11.y=3x2+6x+9
【解析】因为a:b:c=1:2:3,则抛物线的解析式,根据顶点坐标公式可得:y的最值为,则可得: ,解得 (舍去),所以抛物线的解析式为: ,故答案为: .
12.y=﹣x2﹣1等(答案不唯一)
【解析】【分析】设二次函数解析式为y=ax2+c,将(1,-2)代入解析式,得到关于a、c的关系式,从而推知a、c的值.
详解:∵对称轴为y轴,
∴设二次函数解析式为y=ax2+c,
将(1,-2)代入解析式,得a+c=-2,
不防取a=-1,c=-1,得解析式为y=-x2-1,答案不唯一.
故答案为:y=-x2-1等(答案不唯一).
点睛:此题考查了二次函数的性质,要熟悉对称轴公式、二次函数成立的条件,要注意此题具有开放性,答案不唯一.
13.x2+4x+5
【解析】由于两个函数图象都交于y轴上的同一点,所以c的值相等;两条抛物线的形状及开口方向相同,所以a的值相等;由于两条抛物线关于y轴对称,所以两个函数的b值互为相反数.
解:把y=x2-4x+5中的一次项系数-4变成相反数得到:y=x2+4x+5.
故答案为y=x2+4x+5.
“点睛”本题考查了关于y轴对称的两条抛物线的特征:二次项系数、常数项不变,一次项系数互为相反数.
14.【考点】规律型:数字的变化类.
【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
【点评】此题的关键是找规律,注意当规律难找时,可以用二次函数找.
三 、解答题
15.(1). a=-1 (2). P1(,),P2(-,-).
【分析】(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
解:(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
16.【考点】二次函数的三种形式;二次函数的性质.
【分析】(1)由于二次项系数是1,所以直接加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h求解即可;
(3)先求出方程x2﹣4x+3=0的两根,再根据二次函数的性质即可求解.
解:(1)y=x2﹣4x+3=(x2﹣4x+4)﹣4+3=(x﹣2)2﹣1;
(2)∵y=(x﹣2)2﹣1,
∴对称轴为直线x=2,顶点坐标为(2,﹣1);
(3)解方程x2﹣4x+3=0,得x=1或3.
∵y=x2﹣4x+3,a=1>0,
∴抛物线开口向上,
∴当1<x<3时,函数y<0.
点评: 本题考查了二次函数解析式的三种形式,二次函数的性质,难度适中.利用配方法将一般式转化为顶点式是解题的关键.
17.【考点】二次函数的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【分析】(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;
(3)根据题意可以列出相应的不等式组,从而可以解答本题
解:(1)∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴或,
解得,﹣2≤m≤0或2≤m≤4.
【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
18.【考点】 二次函数的性质;待定系数法求二次函数解析式.
【分析】 (1)当y=2时,则2=x﹣1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2,求出a的值,即可解答.
解:(1)当y=2时,则2=x﹣1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得:
解得:
∴y=x2﹣2x﹣1.
顶点坐标为(1,﹣2).
(3)如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=,
代入B(﹣1,2),则a(﹣1)2=2,
解得:a=2,
∴
点评: 本题考查了二次函数的性质,解集本题的关键是求出二次函数的解析式,并结合图形解决问题.
19.【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式.
【分析】(1)把点(1,0)代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值,从而得到抛物线的表达式;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解:(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<.
28.1.3二次函数y=ax2+bx+c的图像性质同步课时作业(2)
姓名:__________班级:__________考号:__________
一、选择题
1.把二次函数y=x2﹣4x+1化成y=a(x+m)2+k的形式是( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
2.已知二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的表达式为( )
A. y=-3x2-1 B. y=3x2 C. y=3x2+1 D. y=3x2-1
3.把抛物线向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
A. B. C. D.
4.二次函数的图象经过三点,则它的解析式为
A. B.
C. D.
5.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y=(x﹣2)2+3 B. y=(x﹣2)2﹣3
C. y=﹣(x﹣2)2+3 D. y=﹣(x﹣2)2﹣3
6.将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
A.b>8 B.b>﹣8 C.b≥8 D.b≥﹣8
7.对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x 2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x 2﹣8x+2
8.若二次函数的图象经过点(2,0),且其对称轴为,则使函数值成立的的取值范围是( )
A.或 B.≤ ≤ C.≤或≥ D.
二、填空题
9.与抛物线关于轴对称的抛物线解析式是__________.
10.一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为_______.
11.抛物线y=ax2+bx+c中,已知a:b:c=1:2:3,y最小值为6,则此抛物线的解析式为_______.
12.请写出一个图象的对称轴为y轴,开口向下,且经过点(1,﹣2)的二次函数解析式,这个二次函数的解析式可以是_____.
13.如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
14.邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据
1
2
3
4
5
6
…
输出数据
…
那么,当输入数据是7时,输出的数据是 .
三、解答题
15.已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
16.已知抛物线y=x2﹣4x+3.
(1)用配方法将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该抛物线的对称轴和顶点坐标;
(3)直接写出当x满足什么条件时,函数y<0.
17.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
18.在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x﹣1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
19.在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
答案解析
一 、选择题
1.【考点】二次函数的三种形式.
【分析】运用配方法把二次函数的一般式化为顶点式即可.
解:y=x2﹣4x+1
=x2﹣4x+4﹣3
=(x﹣2)2﹣3,
故选:D.
2.D
【解析】∵二次函数图象的顶点坐标为(0,1),图象与轴的交点坐标为和,
∴二次函数图象沿轴翻折后的抛物线的顶坐标为(0,-1),与轴的交点坐标为和,
∴可设新抛物线的表达式为:,代入点可得:,解得,
∴翻折后所得抛物线的表达式为:.
故选D.
点睛:抛物线沿轴翻折后所得新的抛物线表达式为.
3.D
【解析】
试题【分析】根据抛物线的平移规律可得:把抛物线向下平移2个单位,得,再向右平移1个单位,所得到的抛物线是,故选:D.
【考点】抛物线的平移.
4.D
【解析】设该二次函数的解析式为:,则由已知条件可得:
,解得: ,
∴该二次函数的解析式为:.
故选D.
5.C
【解析】抛物线开口向下,顶点是(2,3),所以y=﹣(x﹣2)2+3,选C.
点睛:
求二次函数的解析式
(1)已知二次函数过三个点,利用一般式,y=ax2+bx+c().列方程组求二次函数解析式.
(2)已知二次函数与x轴的两个交点 (,利用双根式,y= ()求二次函数解析式,而且此时对称轴方程过交点的中点, .
(3)已知二次函数的顶点坐标,利用顶点式,()求二次函数解析式.
其中a决定开始方向和大小,顶点坐标是(h,k),对称轴方程是x=h.
(4)已知条件中a,b,c,给定了一个值,则需要列两个方程求解.
(5)已知条件有对称轴,对称轴也可以作为一个方程;如果给定的两个点纵坐标相同 (,则可以得到对称轴方程.
6.【考点】二次函数图象与几何变换;一次函数图象与系数的关系.
【分析】先根据平移原则:上→加,下→减,左→加,右→减写出解析式,再列方程组,有公共点则△≥0,则可求出b的取值.
解:由题意得:平移后得到的二次函数的解析式为:y=(x﹣3)2﹣1,
则,
(x﹣3)2﹣1=2x+b,
x2﹣8x+8﹣b=0,
△=(﹣8)2﹣4×1×(8﹣b)≥0,
b≥﹣8,
故选D.
7.C
【解析】根据题意,设y=a(x?2)2+3,抛物线经过点(3,1),所以a+3=1,a=?2.
因此抛物线的解析式为:y=?2(x?2)2+3=?2x2+8x?5.
故选:C.
8.【考点】二次函数与不等式(组)..
【分析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
二 、填空题
9.
【解析】【分析】把原抛物线解析式转化为顶点式形式,求出顶点坐标,再根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求出描出的抛物线的顶点坐标,然后根据描出的抛物线与原抛物线形状相同,开口方向向下写出解析式即可.
详解:∵,
∴顶点,
∴顶点关于轴,对称点为且开口向下,
∴.
故答案为:.
点睛:此题主要考查了二次函数的图像与性质,关键是求出关键点—顶点的对称坐标,然后根据对称性求出函数的解析式,是常考题.
10.y=﹣2(x+1)2+3 或y=-2x2-4x+1
【解析】由题意可知:该抛物线的解析式为y=?2(x?h)2+k,
又∵顶点坐标(?1,3),
∴y=?2(x+1)2+3=-2x2-4x+1,
故答案为:y=﹣2(x+1)2+3 或y=-2x2-4x+1.
11.y=3x2+6x+9
【解析】因为a:b:c=1:2:3,则抛物线的解析式,根据顶点坐标公式可得:y的最值为,则可得: ,解得 (舍去),所以抛物线的解析式为: ,故答案为: .
12.y=﹣x2﹣1等(答案不唯一)
【解析】【分析】设二次函数解析式为y=ax2+c,将(1,-2)代入解析式,得到关于a、c的关系式,从而推知a、c的值.
详解:∵对称轴为y轴,
∴设二次函数解析式为y=ax2+c,
将(1,-2)代入解析式,得a+c=-2,
不防取a=-1,c=-1,得解析式为y=-x2-1,答案不唯一.
故答案为:y=-x2-1等(答案不唯一).
点睛:此题考查了二次函数的性质,要熟悉对称轴公式、二次函数成立的条件,要注意此题具有开放性,答案不唯一.
13.x2+4x+5
【解析】由于两个函数图象都交于y轴上的同一点,所以c的值相等;两条抛物线的形状及开口方向相同,所以a的值相等;由于两条抛物线关于y轴对称,所以两个函数的b值互为相反数.
解:把y=x2-4x+5中的一次项系数-4变成相反数得到:y=x2+4x+5.
故答案为y=x2+4x+5.
“点睛”本题考查了关于y轴对称的两条抛物线的特征:二次项系数、常数项不变,一次项系数互为相反数.
14.【考点】规律型:数字的变化类.
【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
【点评】此题的关键是找规律,注意当规律难找时,可以用二次函数找.
三 、解答题
15.(1). a=-1 (2). P1(,),P2(-,-).
【分析】(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
解:(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
16.【考点】二次函数的三种形式;二次函数的性质.
【分析】(1)由于二次项系数是1,所以直接加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h求解即可;
(3)先求出方程x2﹣4x+3=0的两根,再根据二次函数的性质即可求解.
解:(1)y=x2﹣4x+3=(x2﹣4x+4)﹣4+3=(x﹣2)2﹣1;
(2)∵y=(x﹣2)2﹣1,
∴对称轴为直线x=2,顶点坐标为(2,﹣1);
(3)解方程x2﹣4x+3=0,得x=1或3.
∵y=x2﹣4x+3,a=1>0,
∴抛物线开口向上,
∴当1<x<3时,函数y<0.
点评: 本题考查了二次函数解析式的三种形式,二次函数的性质,难度适中.利用配方法将一般式转化为顶点式是解题的关键.
17.【考点】二次函数的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【分析】(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;
(3)根据题意可以列出相应的不等式组,从而可以解答本题
解:(1)∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴或,
解得,﹣2≤m≤0或2≤m≤4.
【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
18.【考点】 二次函数的性质;待定系数法求二次函数解析式.
【分析】 (1)当y=2时,则2=x﹣1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2,求出a的值,即可解答.
解:(1)当y=2时,则2=x﹣1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得:
解得:
∴y=x2﹣2x﹣1.
顶点坐标为(1,﹣2).
(3)如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=,
代入B(﹣1,2),则a(﹣1)2=2,
解得:a=2,
∴
点评: 本题考查了二次函数的性质,解集本题的关键是求出二次函数的解析式,并结合图形解决问题.
19.【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式.
【分析】(1)把点(1,0)代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值,从而得到抛物线的表达式;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解:(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<.
姓名:__________班级:__________考号:__________
一、选择题
1.把二次函数y=x2﹣4x+1化成y=a(x+m)2+k的形式是( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
2.已知二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的表达式为( )
A. y=-3x2-1 B. y=3x2 C. y=3x2+1 D. y=3x2-1
3.把抛物线向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
A. B. C. D.
4.二次函数的图象经过三点,则它的解析式为
A. B.
C. D.
5.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y=(x﹣2)2+3 B. y=(x﹣2)2﹣3
C. y=﹣(x﹣2)2+3 D. y=﹣(x﹣2)2﹣3
6.将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
A.b>8 B.b>﹣8 C.b≥8 D.b≥﹣8
7.对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x 2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x 2﹣8x+2
8.若二次函数的图象经过点(2,0),且其对称轴为,则使函数值成立的的取值范围是( )
A.或 B.≤ ≤ C.≤或≥ D.
二、填空题
9.与抛物线关于轴对称的抛物线解析式是__________.
10.一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为_______.
11.抛物线y=ax2+bx+c中,已知a:b:c=1:2:3,y最小值为6,则此抛物线的解析式为_______.
12.请写出一个图象的对称轴为y轴,开口向下,且经过点(1,﹣2)的二次函数解析式,这个二次函数的解析式可以是_____.
13.如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
14.邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据
1
2
3
4
5
6
…
输出数据
…
那么,当输入数据是7时,输出的数据是 .
三、解答题
15.已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
16.已知抛物线y=x2﹣4x+3.
(1)用配方法将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该抛物线的对称轴和顶点坐标;
(3)直接写出当x满足什么条件时,函数y<0.
17.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
18.在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x﹣1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
19.在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
答案解析
一 、选择题
1.【考点】二次函数的三种形式.
【分析】运用配方法把二次函数的一般式化为顶点式即可.
解:y=x2﹣4x+1
=x2﹣4x+4﹣3
=(x﹣2)2﹣3,
故选:D.
2.D
【解析】∵二次函数图象的顶点坐标为(0,1),图象与轴的交点坐标为和,
∴二次函数图象沿轴翻折后的抛物线的顶坐标为(0,-1),与轴的交点坐标为和,
∴可设新抛物线的表达式为:,代入点可得:,解得,
∴翻折后所得抛物线的表达式为:.
故选D.
点睛:抛物线沿轴翻折后所得新的抛物线表达式为.
3.D
【解析】
试题【分析】根据抛物线的平移规律可得:把抛物线向下平移2个单位,得,再向右平移1个单位,所得到的抛物线是,故选:D.
【考点】抛物线的平移.
4.D
【解析】设该二次函数的解析式为:,则由已知条件可得:
,解得: ,
∴该二次函数的解析式为:.
故选D.
5.C
【解析】抛物线开口向下,顶点是(2,3),所以y=﹣(x﹣2)2+3,选C.
点睛:
求二次函数的解析式
(1)已知二次函数过三个点,利用一般式,y=ax2+bx+c().列方程组求二次函数解析式.
(2)已知二次函数与x轴的两个交点 (,利用双根式,y= ()求二次函数解析式,而且此时对称轴方程过交点的中点, .
(3)已知二次函数的顶点坐标,利用顶点式,()求二次函数解析式.
其中a决定开始方向和大小,顶点坐标是(h,k),对称轴方程是x=h.
(4)已知条件中a,b,c,给定了一个值,则需要列两个方程求解.
(5)已知条件有对称轴,对称轴也可以作为一个方程;如果给定的两个点纵坐标相同 (,则可以得到对称轴方程.
6.【考点】二次函数图象与几何变换;一次函数图象与系数的关系.
【分析】先根据平移原则:上→加,下→减,左→加,右→减写出解析式,再列方程组,有公共点则△≥0,则可求出b的取值.
解:由题意得:平移后得到的二次函数的解析式为:y=(x﹣3)2﹣1,
则,
(x﹣3)2﹣1=2x+b,
x2﹣8x+8﹣b=0,
△=(﹣8)2﹣4×1×(8﹣b)≥0,
b≥﹣8,
故选D.
7.C
【解析】根据题意,设y=a(x?2)2+3,抛物线经过点(3,1),所以a+3=1,a=?2.
因此抛物线的解析式为:y=?2(x?2)2+3=?2x2+8x?5.
故选:C.
8.【考点】二次函数与不等式(组)..
【分析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
二 、填空题
9.
【解析】【分析】把原抛物线解析式转化为顶点式形式,求出顶点坐标,再根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求出描出的抛物线的顶点坐标,然后根据描出的抛物线与原抛物线形状相同,开口方向向下写出解析式即可.
详解:∵,
∴顶点,
∴顶点关于轴,对称点为且开口向下,
∴.
故答案为:.
点睛:此题主要考查了二次函数的图像与性质,关键是求出关键点—顶点的对称坐标,然后根据对称性求出函数的解析式,是常考题.
10.y=﹣2(x+1)2+3 或y=-2x2-4x+1
【解析】由题意可知:该抛物线的解析式为y=?2(x?h)2+k,
又∵顶点坐标(?1,3),
∴y=?2(x+1)2+3=-2x2-4x+1,
故答案为:y=﹣2(x+1)2+3 或y=-2x2-4x+1.
11.y=3x2+6x+9
【解析】因为a:b:c=1:2:3,则抛物线的解析式,根据顶点坐标公式可得:y的最值为,则可得: ,解得 (舍去),所以抛物线的解析式为: ,故答案为: .
12.y=﹣x2﹣1等(答案不唯一)
【解析】【分析】设二次函数解析式为y=ax2+c,将(1,-2)代入解析式,得到关于a、c的关系式,从而推知a、c的值.
详解:∵对称轴为y轴,
∴设二次函数解析式为y=ax2+c,
将(1,-2)代入解析式,得a+c=-2,
不防取a=-1,c=-1,得解析式为y=-x2-1,答案不唯一.
故答案为:y=-x2-1等(答案不唯一).
点睛:此题考查了二次函数的性质,要熟悉对称轴公式、二次函数成立的条件,要注意此题具有开放性,答案不唯一.
13.x2+4x+5
【解析】由于两个函数图象都交于y轴上的同一点,所以c的值相等;两条抛物线的形状及开口方向相同,所以a的值相等;由于两条抛物线关于y轴对称,所以两个函数的b值互为相反数.
解:把y=x2-4x+5中的一次项系数-4变成相反数得到:y=x2+4x+5.
故答案为y=x2+4x+5.
“点睛”本题考查了关于y轴对称的两条抛物线的特征:二次项系数、常数项不变,一次项系数互为相反数.
14.【考点】规律型:数字的变化类.
【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
【点评】此题的关键是找规律,注意当规律难找时,可以用二次函数找.
三 、解答题
15.(1). a=-1 (2). P1(,),P2(-,-).
【分析】(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
解:(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
16.【考点】二次函数的三种形式;二次函数的性质.
【分析】(1)由于二次项系数是1,所以直接加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h求解即可;
(3)先求出方程x2﹣4x+3=0的两根,再根据二次函数的性质即可求解.
解:(1)y=x2﹣4x+3=(x2﹣4x+4)﹣4+3=(x﹣2)2﹣1;
(2)∵y=(x﹣2)2﹣1,
∴对称轴为直线x=2,顶点坐标为(2,﹣1);
(3)解方程x2﹣4x+3=0,得x=1或3.
∵y=x2﹣4x+3,a=1>0,
∴抛物线开口向上,
∴当1<x<3时,函数y<0.
点评: 本题考查了二次函数解析式的三种形式,二次函数的性质,难度适中.利用配方法将一般式转化为顶点式是解题的关键.
17.【考点】二次函数的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【分析】(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;
(3)根据题意可以列出相应的不等式组,从而可以解答本题
解:(1)∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴或,
解得,﹣2≤m≤0或2≤m≤4.
【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
18.【考点】 二次函数的性质;待定系数法求二次函数解析式.
【分析】 (1)当y=2时,则2=x﹣1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2,求出a的值,即可解答.
解:(1)当y=2时,则2=x﹣1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得:
解得:
∴y=x2﹣2x﹣1.
顶点坐标为(1,﹣2).
(3)如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=,
代入B(﹣1,2),则a(﹣1)2=2,
解得:a=2,
∴
点评: 本题考查了二次函数的性质,解集本题的关键是求出二次函数的解析式,并结合图形解决问题.
19.【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式.
【分析】(1)把点(1,0)代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值,从而得到抛物线的表达式;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解:(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<.
28.1.3二次函数y=ax2+bx+c的图像性质同步课时作业(2)
姓名:__________班级:__________考号:__________
一、选择题
1.把二次函数y=x2﹣4x+1化成y=a(x+m)2+k的形式是( )
A.y=(x﹣2)2+1 B.y=(x﹣2)2﹣1 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣3
2.已知二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的表达式为( )
A. y=-3x2-1 B. y=3x2 C. y=3x2+1 D. y=3x2-1
3.把抛物线向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
A. B. C. D.
4.二次函数的图象经过三点,则它的解析式为
A. B.
C. D.
5.二次函数的图象如图所示,则这个二次函数的解析式为( )
A. y=(x﹣2)2+3 B. y=(x﹣2)2﹣3
C. y=﹣(x﹣2)2+3 D. y=﹣(x﹣2)2﹣3
6.将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
A.b>8 B.b>﹣8 C.b≥8 D.b≥﹣8
7.对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x 2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x 2﹣8x+2
8.若二次函数的图象经过点(2,0),且其对称轴为,则使函数值成立的的取值范围是( )
A.或 B.≤ ≤ C.≤或≥ D.
二、填空题
9.与抛物线关于轴对称的抛物线解析式是__________.
10.一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为_______.
11.抛物线y=ax2+bx+c中,已知a:b:c=1:2:3,y最小值为6,则此抛物线的解析式为_______.
12.请写出一个图象的对称轴为y轴,开口向下,且经过点(1,﹣2)的二次函数解析式,这个二次函数的解析式可以是_____.
13.如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
14.邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据
1
2
3
4
5
6
…
输出数据
…
那么,当输入数据是7时,输出的数据是 .
三、解答题
15.已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
16.已知抛物线y=x2﹣4x+3.
(1)用配方法将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该抛物线的对称轴和顶点坐标;
(3)直接写出当x满足什么条件时,函数y<0.
17.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
18.在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x﹣1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
19.在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
答案解析
一 、选择题
1.【考点】二次函数的三种形式.
【分析】运用配方法把二次函数的一般式化为顶点式即可.
解:y=x2﹣4x+1
=x2﹣4x+4﹣3
=(x﹣2)2﹣3,
故选:D.
2.D
【解析】∵二次函数图象的顶点坐标为(0,1),图象与轴的交点坐标为和,
∴二次函数图象沿轴翻折后的抛物线的顶坐标为(0,-1),与轴的交点坐标为和,
∴可设新抛物线的表达式为:,代入点可得:,解得,
∴翻折后所得抛物线的表达式为:.
故选D.
点睛:抛物线沿轴翻折后所得新的抛物线表达式为.
3.D
【解析】
试题【分析】根据抛物线的平移规律可得:把抛物线向下平移2个单位,得,再向右平移1个单位,所得到的抛物线是,故选:D.
【考点】抛物线的平移.
4.D
【解析】设该二次函数的解析式为:,则由已知条件可得:
,解得: ,
∴该二次函数的解析式为:.
故选D.
5.C
【解析】抛物线开口向下,顶点是(2,3),所以y=﹣(x﹣2)2+3,选C.
点睛:
求二次函数的解析式
(1)已知二次函数过三个点,利用一般式,y=ax2+bx+c().列方程组求二次函数解析式.
(2)已知二次函数与x轴的两个交点 (,利用双根式,y= ()求二次函数解析式,而且此时对称轴方程过交点的中点, .
(3)已知二次函数的顶点坐标,利用顶点式,()求二次函数解析式.
其中a决定开始方向和大小,顶点坐标是(h,k),对称轴方程是x=h.
(4)已知条件中a,b,c,给定了一个值,则需要列两个方程求解.
(5)已知条件有对称轴,对称轴也可以作为一个方程;如果给定的两个点纵坐标相同 (,则可以得到对称轴方程.
6.【考点】二次函数图象与几何变换;一次函数图象与系数的关系.
【分析】先根据平移原则:上→加,下→减,左→加,右→减写出解析式,再列方程组,有公共点则△≥0,则可求出b的取值.
解:由题意得:平移后得到的二次函数的解析式为:y=(x﹣3)2﹣1,
则,
(x﹣3)2﹣1=2x+b,
x2﹣8x+8﹣b=0,
△=(﹣8)2﹣4×1×(8﹣b)≥0,
b≥﹣8,
故选D.
7.C
【解析】根据题意,设y=a(x?2)2+3,抛物线经过点(3,1),所以a+3=1,a=?2.
因此抛物线的解析式为:y=?2(x?2)2+3=?2x2+8x?5.
故选:C.
8.【考点】二次函数与不等式(组)..
【分析】由抛物线与x轴的交点及对称轴求出另一个交点坐标,根据抛物线开口向下,根据图象求出使函数值y>0成立的x的取值范围即可.
解:∵二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,
∴二次函数的图象与x轴另一个交点为(﹣4,0),
∵a<0,
∴抛物线开口向下,
则使函数值y>0成立的x的取值范围是﹣4<x<2.
二 、填空题
9.
【解析】【分析】把原抛物线解析式转化为顶点式形式,求出顶点坐标,再根据关于x轴对称的点的横坐标相同,纵坐标互为相反数求出描出的抛物线的顶点坐标,然后根据描出的抛物线与原抛物线形状相同,开口方向向下写出解析式即可.
详解:∵,
∴顶点,
∴顶点关于轴,对称点为且开口向下,
∴.
故答案为:.
点睛:此题主要考查了二次函数的图像与性质,关键是求出关键点—顶点的对称坐标,然后根据对称性求出函数的解析式,是常考题.
10.y=﹣2(x+1)2+3 或y=-2x2-4x+1
【解析】由题意可知:该抛物线的解析式为y=?2(x?h)2+k,
又∵顶点坐标(?1,3),
∴y=?2(x+1)2+3=-2x2-4x+1,
故答案为:y=﹣2(x+1)2+3 或y=-2x2-4x+1.
11.y=3x2+6x+9
【解析】因为a:b:c=1:2:3,则抛物线的解析式,根据顶点坐标公式可得:y的最值为,则可得: ,解得 (舍去),所以抛物线的解析式为: ,故答案为: .
12.y=﹣x2﹣1等(答案不唯一)
【解析】【分析】设二次函数解析式为y=ax2+c,将(1,-2)代入解析式,得到关于a、c的关系式,从而推知a、c的值.
详解:∵对称轴为y轴,
∴设二次函数解析式为y=ax2+c,
将(1,-2)代入解析式,得a+c=-2,
不防取a=-1,c=-1,得解析式为y=-x2-1,答案不唯一.
故答案为:y=-x2-1等(答案不唯一).
点睛:此题考查了二次函数的性质,要熟悉对称轴公式、二次函数成立的条件,要注意此题具有开放性,答案不唯一.
13.x2+4x+5
【解析】由于两个函数图象都交于y轴上的同一点,所以c的值相等;两条抛物线的形状及开口方向相同,所以a的值相等;由于两条抛物线关于y轴对称,所以两个函数的b值互为相反数.
解:把y=x2-4x+5中的一次项系数-4变成相反数得到:y=x2+4x+5.
故答案为y=x2+4x+5.
“点睛”本题考查了关于y轴对称的两条抛物线的特征:二次项系数、常数项不变,一次项系数互为相反数.
14.【考点】规律型:数字的变化类.
【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
【点评】此题的关键是找规律,注意当规律难找时,可以用二次函数找.
三 、解答题
15.(1). a=-1 (2). P1(,),P2(-,-).
【分析】(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
解:(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
16.【考点】二次函数的三种形式;二次函数的性质.
【分析】(1)由于二次项系数是1,所以直接加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h求解即可;
(3)先求出方程x2﹣4x+3=0的两根,再根据二次函数的性质即可求解.
解:(1)y=x2﹣4x+3=(x2﹣4x+4)﹣4+3=(x﹣2)2﹣1;
(2)∵y=(x﹣2)2﹣1,
∴对称轴为直线x=2,顶点坐标为(2,﹣1);
(3)解方程x2﹣4x+3=0,得x=1或3.
∵y=x2﹣4x+3,a=1>0,
∴抛物线开口向上,
∴当1<x<3时,函数y<0.
点评: 本题考查了二次函数解析式的三种形式,二次函数的性质,难度适中.利用配方法将一般式转化为顶点式是解题的关键.
17.【考点】二次函数的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【分析】(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;
(3)根据题意可以列出相应的不等式组,从而可以解答本题
解:(1)∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴或,
解得,﹣2≤m≤0或2≤m≤4.
【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
18.【考点】 二次函数的性质;待定系数法求二次函数解析式.
【分析】 (1)当y=2时,则2=x﹣1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2,求出a的值,即可解答.
解:(1)当y=2时,则2=x﹣1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得:
解得:
∴y=x2﹣2x﹣1.
顶点坐标为(1,﹣2).
(3)如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=,
代入B(﹣1,2),则a(﹣1)2=2,
解得:a=2,
∴
点评: 本题考查了二次函数的性质,解集本题的关键是求出二次函数的解析式,并结合图形解决问题.
19.【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式.
【分析】(1)把点(1,0)代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值,从而得到抛物线的表达式;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解:(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<.
